 |
В2. Сколько различных трёхзначных чисел можно составить из цифр 0, 1, 2 так, чтобы в каждом числе не было одинаковых цифр
|
|
|
|
Ответ______________________________ (6)
В3. Найти наибольшее значение функции у = х2 – 4х + 6, если хϵ[0; 3]
Ответ______________________________ (6)
ОУ _________________________________________________________________________________
Курс _____ Группа ______________________ № (по списку)_________________________________
Математика Вариант 2
1. Что называется функцией?
1) Заданное число;
2) Правило, по которому каждому значению аргумента х в соответствует одно и только одно значение функции у;
3) Векторы, расположенные на параллельных прямых;
4) Определитель третьего порядка.
2. Последовательность задана формулой общего элемента хn= n3.Определите первые три члена этой последовательности:
1) 0; 1; 3;
2) 1; 4; 9;
3) 2; 6; 8;
4) 1; 8; 27.
3. Найти значение предела  .
.
1) 3;
2) 1;
3) 0;
4) 2.
4. Чему равно значение предела  ?
?
1) 0;
2)  ;
;
3)  ;
;
4) 1.
5. Найти значение прдела  .
.
1) ∞;
2) 0;
3) 2;
4) 3.
6. Найти производную функции у = (2 – 5х)10.
1) у' = –20(2 – 5х)9;
2) у' = 10(2 – 5х)9;
3) у' = – 50х(2 – 5х)9;
4) у' = –50(2 – 5х)9.
7. Чему равна производная частного  ?
?
1) 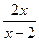 ;
;
2)  ;
;
3)  ;
;
4) 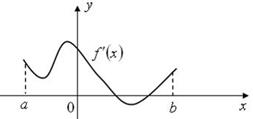
 .
.
8. На рисунке представлена функция y = f(x), заданная на отрезке [a; b]. Сколько точек экстремума имеет функция?
1) 1;
2) 2;
3) 3;
4) 4.
9. Вычислить неопределенный интеграл 
1) – ln|cosx| + C;
2) – ln|sinx| + C;
3) tgx +C;
4) ctgx + C.
Чем определяется порядок дифференциального уравнения?
1) Количеством операций (шагов) при его решении;
2) Количеством переменных величин в правой части;
3) Максимальной степенью переменной х;
Высшим порядком производной, входящей в уравнение.
11. Какое решение имеет дифференциальное уравнение первого порядка с разделяющимися переменными хdy = уdx?
1) у = 0,5х2 + С;
2) у = х∙С;
3) у = ех +С;
4) lnу = х + 2С.
12. Дано дифференциальное уравнение  . Найдите соотвествующее ему характерестическое уравнение.
. Найдите соотвествующее ему характерестическое уравнение.
|
|
|
1)  ;
;
2)  ;
;
3)  ;
;
4)  .
.
13. Укажите общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, если его характеристическое уравнение к2 – 4?
1)  ;
;
2) 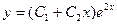 ;
;
3)  ;
;
4)  .
.
Чему равна вероятность невозможного события?
1) любому значению из промежутка [0; 1];
2) 0,5;
3) 0;
4) 1.
Брошена наугад игральная кость. Какова вероятность того, что выпадет нечетное число очков?
1) 25%;
2) 30%;
3) 50%;
4) 75%.
Ответы на задания В1, В2 и В3 запишите в указанном месте, а затем впишите в бланк тестирования справа от номера задания (В1, В2 или В3), начиная с первой клеточки.
В1. Найти значение определенного интеграла  .
.
Ответ______________________________ (27)
В2. Энциклопедия состоит из пяти томов – с первого по пятый. Сколькими способами её можно поставить на полке?
Ответ______________________________ (120)
В3. Найти наибольшее значение функции у = 2х – х2 + 2, если хϵ[0; 3]
Ответ______________________________ (3)
ОУ _________________________________________________________________________________
Курс _____ Группа ______________________ № (по списку)_________________________________
Математика Вариант 3
Какой из перечисленных способов не является способом задания функции?
1) Аналитический;
2) Графический;
3) Табличный;
Матричный.
2. Последовательность задана формулой общего элемента хn= n4.Определите первые три члена этой последовательности:
1) 2; 6; 8;
2) 1; 4; 9;
3) 1; 8; 27;
4) 1; 16; 81.
3. Чему равно значение предела  ?
?
1) 0;
2) 2;
3)  ;
;
4) 1.
4. Найти значение предела 
1) е4/5;
2)  ;
;
3) 1;
4) ∞.
5. Чему равно значение предела  ?
?
1) 3;
2)  ;
;
3) 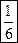 ;
;
4) 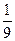 .
.
6. Найти производную функции у = (2х – 5)15.
1) у' = 15(2х – 5)14 ;
2) у' = 30(2х – 5)14;
3) у' = (2х – 5)14;
4) у' = –30(2х – 5)14.
7. Найти производную функции у(х) = ех – 4х2.
1) ех – 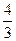 х3;
х3;
2) ех – 8х;
3) ех – 2х;
4)  ех – 4х.
ех – 4х.
8. На рисунке задана функция у = f (x). Какому промежутку, принадлежат все точки экстремума?
1) [-3; 2];
2) (– ∞; +∞);
3) (0; 2];
4) [-3; 0).
9. Выберите замену при вычислении неопределенного интеграла 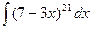 .
.
|
|
|
1) t = 3x;
2) t = 7 – 3x;
3) t = (7 – 3x)21;
4) t =  x.
x.
Укажите дифференциальное уравнение первого порядка с разделяющимися переменными.
1) (х + 3)dх – хуdу = 0;
2) у3sin2х – у// = 0;
3) у///– ху2 = 2ху;
4) х2 – 5х + 6 = 0.
11. Какое решение имеет дифференциальное уравнение первого порядка с разделяющимися переменными dy = х2dx?
1) у =  ;
;
2) у =  + С;
+ С;
3) у = е3х +С;
4) lnу = х3 + 3С.
12. Дано дифференциальное уравнение  . Найдите соотвествующее ему характерестическое уравнение.
. Найдите соотвествующее ему характерестическое уравнение.
1) 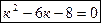 ;
;
2) 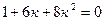 ;
;
3)  ;
;
4)  .
.
13. Укажите общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, если его характеристическое уравнение к2 + 4?
1)  ;
;
2) 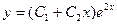 ;
;
3)  ;
;
4)  .
.
14. Какое событие называется случайным?
1) нельзя утверждать, что это событие непременно произойдет;
2) можно утверждать, что это событие непременно произойдет;
3) нельзя утверждать, что это событие;
4) среди указанных ответов нет верного.
Брошена наугад игральная кость. Какова вероятность того, что выпадет четное число очков?
1) 25%;
2) 30%;
3) 50%;
4) 75%.
Ответы на задания В1, В2 и В3 запишите в указанном месте, а затем впишите в бланк тестирования справа от номера задания (В1, В2 или В3), начиная с первой клеточки.
В1. Найти значение определенного интеграла 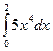 .
.
Ответ______________________________ (32)
|
|
|


