 |
Свободные колебания систем с одной степенью свободы при наличии затухания
|
|
|
|
Формулы, полученные в предыдущем подразделе, относятся к случаю отсутствия поглощения (диссипации) механической энергии в процессе движения системы. В таких системах после исчезновения возмущающих нагрузок механическая энергия остается постоянной, вследствие чего колебания с течением времени не затухают. Механическая система, при движении которой механическая энергия остается постоянной, называется консервативной, если же механическая энергия при движении уменьшается, система называется диссипативной.
Для учета сил, вызывающих поглощение энергии (диссипативных сил) в уравнение движения необходимо ввести дополнительное слагаемое, учитывающее силы неупругого сопротивления движению. Из-за многообразия сил сопротивления (внешнего сухого и вязкого трения, внутреннего трения в материале и т. п.), и представления их различными моделями неупругого сопротивления (линейными и нелинейными, зависящими и независящими от частоты или амплитуды и т. д.), невозможно однозначно ввести диссипативное слагаемое в уравнение движения.
В настоящее время нормативными документами рекомендуется использовать физически реализуемые, частотно-независимые модели сопротивления. К таким моделям относятся скорректированная модель Фохта (вязкого трения) и частотно-независимая модель внутреннего трения. В частности, сила сопротивления при использовании скорректированной модели Фохта [6] принята в виде
, (2.15)
где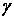 
– нормативный коэффициент потерь, характеризующий затухание.
В практических расчетах используются коэффициенты потерь, рекомендуемые значения которых приведены в табл. 2.1. Знак минус в (2.15) указывает, что силы сопротивления имеют направление, противоположное скорости движения.
|
|
|
Масса в процессе колебаний (рис. 2.3) будет находиться в равновесии под действием сил упругости, инерции и сопротивления, так что
или 
(2.16)
Выражение (2.16) представляет дифференциальное уравнение затухающих колебаний системы с одной степенью свободы.
Обозначая 
, получим
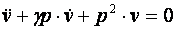. (2.17)
Рис. 2.3. Свободные колебания диссипативной системы
Решение данного уравнения можно представить в виде
или
, (2.18)
где e – основание натуральных логарифмов ( 
= 2,718);
– круговая частота затухающих свободных колебаний.
Используя начальные условия 
получим начальную амплитуду свободных колебаний
(2.19)
и начальную фазу колебаний
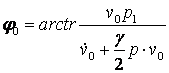, (2.20)
где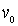 
– начальное перемещение, 
– начальная скорость колебаний.
Период, то есть продолжительность полного цикла колебаний в секунду, составляет
(2.21)
График свободных затухающих колебаний показан на рис. 2.4.
Рис. 2.4. График свободных колебаний диссипативной системы
Колебания системы при наличии сил сопротивления затухают, убывая по закону геометрической прогрессии. Для оценки скорости затухающих колебаний используется так называемый логарифмический декремент
колебаний 
. (2.22)
Для реальных конструкций, как правило, 
, и поэтому при определении частоты и периода затухающих колебаний сопротивление среды можно не учитывать.
Резона́нс (фр. resonance, от лат. resono «откликаюсь») — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при совпадении частоты собственных колебаний с частотой колебаний вынуждающей силы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с некоторой другой частотой, определяемой из параметров колебательной системы, таких как внутренняя (собственная) частота, коэффициент вязкости и т. п
|
|
|
|
|
|
