 |
На какие классы делятся СМО?
|
|
|
|
СМО Вариант 2.
Задание 1. Рассматривается классическая задача Эрланга. Известно, что заявки на телефонные переговоры в переговорный пункт поступают с интенсивностью, равной 90 заявок в час, а средняя продолжительность разговора по телефону составляет 2 минуты.
Определить показатели эффективности работы СМО (телефонной станции) при наличии одного телефонного номера. Найти оптимальное число телефонных номеров (условием оптимальности считать удовлетворение 90% переговоров, т.е. относительная пропускная способность должна быть не меньше 0,9).
Решение:
При наличии одного телефонного номера исчисляем показатели обслуживания как для одноканальной СМО.
Интенсивность потока обслуживания
 .
.
Интенсивность нагрузки. ρ = λ * tобс = 90 * 2/60 = 3. Интенсивность нагрузки ρ=3 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания.
Вероятность, что канал свободен (доля времени простоя канала).

Следовательно, 25%в течение часа канал будет не занят, время простоя соответственно равноtпр = 15 мин.
Доля заявок, получивших отказ (вероятность отказа).
pотк = 1 - p0 = 1 – 0,25 = 0,75
Значит, 75% из числа поступивших заявок не принимаются к обслуживанию.
Относительная пропускная способность.Доля обслуживаемых заявок, поступающих в единицу времени:
Q= p0 = 0,25
Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок).
А = Q* λ = 0,25 * 90 = 22,5 заявок/част.е. в среднем в час будут обслужены 22,5 заявки.
Очевидно, что при наличии только одного телефонного номера СМО будет плохо справляться с потоком заявок.
Будем постепенно увеличиватьчисло каналов(телефонных номеров) n = 2, 3, 4,... и определим по формулам для получаемой n-канальной СМО характеристики обслуживания.
|
|
|
При n = 2 
 ;
; 
При n = 3 
 ;
; 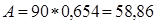
При n = 4 
 ;
; 
При n = 5 
 ;
; 
При n = 6 
 ;
; 
Значения характеристик СМО представим в таблице:
| Характеристика обслуживания | Число каналов (телефонных номеров) | |||||
| Относит.пропускная способность,Q | 0,25 | 0,471 | 0,654 | 0,794 | 0,89 | 0,948 |
| Абсолют.пропускная способность, А | 22,5 | 42,39 | 58,86 | 71,46 | 80,1 | 85,32 |
По условию оптимальности q ≥ 0,9, следовательно, необходимо установить 6 телефонных номеров (в этом случае q = 0,948). При этом в часбудут обслуживаться в среднем 85 заявок (Q = 85,32), а среднее число занятых телефонных номеров (каналов)

Задание 2.
Интенсивность посещения телефонного узла, состоящего из трех телефонных аппаратов, составляет 0,5 человек в минуту; средняя продолжительность одного телефонного разговора составляет 5,8 минут; посетитель покидает телефонный узел, если в очереди находится 3 человека.
Требуется определить значения характеристик СМО при исходных данных, а также найти оптимальную длину очереди (чтобы обслуживалось более 90% заявок).
Решение:
Рассчитаем показатели обслуживания многоканальной СМО с ограниченной длиной очереди:
Интенсивность потока обслуживания составляет:

Интенсивность нагрузки.ρ = λ *tобс = 0,5 * 5,8 = 2,9
Интенсивность нагрузки ρ=2,9 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания.
Поскольку 2,9<3, то процесс обслуживания будет стабилен.
Вероятность, что канал свободен (доля времени простоя каналов).


 ,24% в течение часа канал будет не занят, время простоя равно tпр = 0,0424*60 = 2,5 мин.
,24% в течение часа канал будет не занят, время простоя равно tпр = 0,0424*60 = 2,5 мин.
Вероятность отказа (Доля заявок, получивших отказ).

Значит, 15,6% из числа поступивших заявок не принимаются к обслуживанию.
|
|
|
Вероятность обслуживания поступающих заявок (вероятность того, что клиент будет обслужен).
В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому: pотк + pобс = 1
pобс = 1 - pотк = 1 – 0,156 = 0,844
Относительная пропускная способность: Q = pобс = 0,844.
Следовательно, 84,4% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%.
Будем постепенно увеличивать длину очереди, чтобы найти оптимальный вариант
m = 4
Вероятность, что канал свободен.

Следовательно, 3,69% в течение часа канал будет не занят, время простоя равно tпр = 0,0369*60 = 2,2 мин.
Вероятность отказа.

Значит, 13,1 % из числа поступивших заявок не принимаются к обслуживанию.
Вероятность обслуживания поступающих заявок.
pобс = 1 - pотк = 1 – 0,131 = 0,869
Относительная пропускная способность: Q= pобс = 0,869.
Следовательно, 86,9% из числа поступивших заявок будут обслужены.
m = 5
Вероятность, что канал свободен.

Следовательно, 3,27% в течение часа канал будет не занят, время простоя равно tпр = 0,0327*60 = 2 мин.
Вероятность отказа.

Значит, 11,2 % из числа поступивших заявок не принимаются к обслуживанию.
Вероятность обслуживания поступающих заявок.
pобс = 1 - pотк = 1 – 0,112 = 0,888
Относительная пропускная способность: Q = pобс = 0,888.
Следовательно, 88,8% из числа поступивших заявок будут обслужены.
m = 6
Вероятность, что канал свободен.

Следовательно, 2,95% в течение часа канал будет не занят, время простоя равно tпр = 0,0295*60 = 1,8 мин.
Вероятность отказа.

Значит, 9,8 % из числа поступивших заявок не принимаются к обслуживанию.
Вероятность обслуживания поступающих заявок.
pобс = 1 - pотк = 1 – 0,098 = 0,902
Относительная пропускная способность: q = pобс = 0,902.
Следовательно, 90,2% из числа поступивших заявок будут обслужены.
По условию оптимальности q ≥ 0,9, следовательно, необходимо установить очередь в 6 человек (в этом случае q = 0,902).
Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок).
A = pобс * λ = 0,902 * 0,5 = 0,451 заявок/мин.
Среднее время простоя СМО.
tпр = pотк *tобс = 0,098* 5,8 = 0,568 мин.
Среднее число обслуживаемых заявок.
Lобс = ρ * Q = 2,9 * 0,902 = 2,616 ед/мин.
Задание 3.
Имеется веб-система с пятью серверами, которые обрабатывают запросы, поступающие с интенсивностью 10 http-запросов в секунду. Среднее время обслуживания равно среднему времени выборки данных с жесткого диска и составляет 0,25с. Если все сервера заняты, запрос становится в очередь и ожидает обслуживания.
|
|
|
Найти вероятность того, что запросы отсутствуют (все каналы обслуживания свободны), вероятность того, что заняты все серверы, вероятность отказа в обслуживании запроса, относительную и абсолютную пропускные способности веб-системы.
Решение:
Это будет многоканальная СМО с неограниченной очередью
Интенсивность потока обслуживания: 
Интенсивность нагрузки: ρ = λ *tобс = 10 * 0,25 = 2,5
Интенсивность нагрузки ρ=2,5 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания.
Поскольку 2,5<5, то процесс обслуживания будет стабилен.
Вероятность, что канал свободен (доля времени простоя серверов).


Следовательно, вероятность того, что канал будет не занят равна 8,01%.
Вероятность того, что все каналы заняты: 
Вероятность отказа (Доля заявок, получивших отказ).
Поскольку отказ в обслуживании в таких системах не может быть, то pотк = 0
Вероятность обслуживания поступающих заявок (вероятность того, что клиент будет обслужен).pобс = 1 – pотк = 1 – 0 = 1pобс = 1 – pотк = 1 – 0 = 1
Относительная пропускная способность: Q = pобс = 1.
Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок).
A = λ*Q = 10*1 = 10 заявок/сек.
Задание 4.
Что такое СМО?
Системой массового обслуживания (СМО) называется любая система для выполнения заявок, поступающих в неё в случайные моменты времени.
На какие классы делятся СМО?
Основные классы СМО следующие:
1.Системы с отказами (с потерями).
2.Системы с ожиданием (с очередью).
|
|
|


