 |
Экспертная оценка надежности машин
|
|
|
|
При оценке надежности машин и их элементов экспертные методы используют для решения задач двух типов:
• определения значений показателей надежности в условиях, когда применение других методов невозможно или нецелесообразно по экономическим соображениям;
• ранжирования случайных величин (показателей надежности; факторов, определяющих надежность изделий; элементов, лимитирующих надежность машин, и др.) в порядке значимости.
Методы экспертной оценки чаще всего используют в ситуациях, когда достоверность исходной информации невелика. Эти методы являются вероятностными. Они основаны на способности специалиста давать полезную информацию в условиях неопределенности. Неизвестную количественную характеристику надежности рассматривают в таких условиях как случайную величину, отражением закона распределения которой является индивидуальная оценка достоверности или значимости того или иного события. Когда такие оценки получены от группы экспертов, то предполагают, что «истинное» значение исследуемой характеристики находится внутри диапазона оценок и что «обобщенное» коллективное мнение является более достоверным.
Для анализа группового мнения используют средние величины:
– среднюю арифметическую оценку
(9.1)
– или среднюю взвешенную оценку
(9.2)
где vi — веса оценок при i = 1,2,... n; n — число экспертов или число контролируемых ими дефектов.
Оценки, полученные от экспертов, могут быть расположены в порядке возрастания или убывания показателя. Если необходимо установить значение показателя, которое находится в середине упорядоченного ряда, рассчитывают медиану.
Медиану можно предпочесть средней арифметической, так как на нее меньше влияют крайние точки ряда. Кроме того, в большинстве случаев медиана более устойчива и менее подвержена случайностям подбора экспертов, чем средняя арифметическая.
|
|
|
При анализе экспертных оценок особенно важна вариация значений около средней оценки, поскольку, чем меньше рассеяны оценки, тем точнее средние значения будут отражать групповое мнение. Для приближенной характеристики вариации ряда может быть вычислена амплитуда:
(9.3)
Для упорядоченного ряда могут быть рассчитаны квартили, т. е. значения Q1, Q2 и Q3, выбранные так, что 25 % оценок оказываются ниже Q, (меньше его); 25 % заключены между Q1, и Q2; 25 % — между Q2, и Q3; а остальные 25 % превосходят Q3.
Если значения квартилей приближаются к медиане, это означает, что распределение оценок характеризуется малым рассеянием. Следовательно, за показатель вариации принимают отклонение квартилей от медианы. Медиану применяют тогда, когда существуют значительные колебания в оценках, полученных от разных экспертов. В остальных случаях используют среднюю арифметическую оценку.
Существует несколько способов проведения опроса экспертов. Один из них (метод согласования) заключается в том, что каждый эксперт дает оценку независимо от других, а затем эти оценки объединяют в одну обобщенную (согласованную) с помощью одного из статистических методов.
Второй способ (групповой) основан на совместной работе экспертов и получении суммарной оценки от всей группы в целом.
При третьем способе (метод Дельф) согласование индивидуальных оценок сочетается с последовательным ознакомлением каждого эксперта с оценками остальных.
Наиболее распространен опрос группы экспертов по методу согласования оценок. В этом случае обобщенная оценка
(9.4)
где рi — оценка i -ro эксперта; n — число экспертов.
Средняя взвешенная оценка
(9.5)
где Ri — вес, приписываемый мнению i -ro эксперта.
|
|
|
Вес мнения каждого эксперта определяют на основе оценок его предыдущей деятельности, например, степени надежности, или с учетом квалификации, эрудиции, должности или академического звания эксперта (табл. 9.2).
Опрашивать экспертов можно заочно, когда личный контакт аналитиков с экспертами отсутствует, или очно, когда эксперты заполняют анкету в присутствии аналитиков. Преимуществами заочного опроса является его относительная простота и дешевизна; однако, тут возможны ошибки при заполнении анкет. При личной беседе этот недостаток исключается, но требуются значительные затраты труда и времени. Кроме того, аналитик, проводящий личный опрос, может сознательно или невольно влиять на ответы эксперта.
Иногда рекомендуется опрашивать экспертов в несколько туров. Это позволяет экспертам «взвесить» свои суждения с учетом ответов и доводов коллег и дополнительной информации, которая не была учтена в предыдущем туре.
Методика обработки результатов экспертной оценки надежности зависит от типа решаемых задач. Если в результате экспертной оценки производится ранжирование показателей для определения их относительной значимости (например, задача расположения элементов машины в порядке убывания одного из показателей надежности), полученные данные обрабатывают таким образом:
1. Вычисляют сумму рангов 
для каждого показателя.
2. Определяют среднее значение суммы рангов по всем факторам и для всех экспертов:
(9.6)
3. Вычисляют отклонение суммы рангов каждого фактора от общего среднего ранга:
(9.7)
4. Определяют сумму квадратов отклонений:
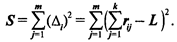
В зависимости от суммы рангов каждому показателю присваивают общий ранг.
6. Проверяют степень согласованности мнений экспертов с помощью критерия Кендалла — W-статистики:
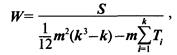(9.9)
где m — число экспертов; k — число ранжируемых показателей; Ti — коэффициент, зависящий от компетентности специалистов.
Этот коэффициент
где tij — число показателей, которым i -й эксперт присвоил одинаковый ранг.
Коэффициент конкордации подчиняется X2 -распределению. Гипотезу о наличии согласованности мнений специалистов принимают, если выполняется условие 
, где 
— квантиль X2 -распределения, соответствующий уровню значимости а и числу степеней свободы (k — 1).
|
|
|
При определении значений показателей надежности результаты экспертной оценки обрабатывают обычным порядком. Использование экспертных методов помогает формализовать процедуру сбора, обобщения и анализа мнений специалистов для преобразования их в форму, более удобную для принятия обоснованного решения.
Наиболее важной проблемой совершенствования экспертных методов является повышение их надежности (достоверности результатов оценки). Решение этой проблемы требует большой экспериментальной и аналитической работы, результатами которой должны быть:
– выяснение соответствия между вопросами и оценками;
– выявление возможных «скрытых» факторов, влияющих на суждение экспертов;
– исследование форм обратной связи между экспертами и аналитиками; создание методов, позволяющих объективно оценить степень обоснованности ответов экспертов.
|
|
|
