 |
Построение эквивалентной схемы заданной цепи для рабочего диапазона частот
|
|
|
|
Задание и исходные данные
1. Письменное объяснение работы схемы назначение всех элементов схемы;
2. 
Изобразить эквивалентную схему заданной цепи для рабочего диапазона частот;
3. Определить параметры линейной схемы замещения на резонансной частоте контура;
4. Найти передаточную функцию цепи по напряжению, построить АЧХ и ФЧХ схемы для рабочего диапазона частот;
5. Определить импульсную характеристику цепи. Построить графики её огибающих и аргумента;
6. Рассчитать построить АЧ и ФЧ спектры заданного управляющего сигнала. Записать аналитическое выражения для АМ-сигнала с модуляцией по закону заданного управляющего сигнала. Вид модуляции – балансовая. Записать функцию спектральной плотности сигнала, построить график АЧ-спектра и ФЧ-спектра.
7. Найти отклик схемы при воздействии на ее вход АМ-сигнала.
Исходные данные:
Параметры схемы
L1=180мкГн;
L2=800мкГн;
C1 = 1000пФ;
C3 = 100пФ;
С3 = 2,2мкФ;
R1 = 150кОм;
Rн = 91кОм;
Сн = 30пФ;
QL = 100
Параметры транзистора:
СЗИ = 12пФ;
СЗС = 5пФ;
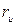= 200Ом;
R = 90 кОм;
S = 3мСм.
Управляющий сигнал:
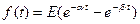где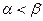 
Значения для балансовой модуляции:
Umax колеб.=0,2В, начальная фаза несущей частоты 0, несущая частота равна частоте максимума АЧХ схемы.
1. 
Анализ схемы
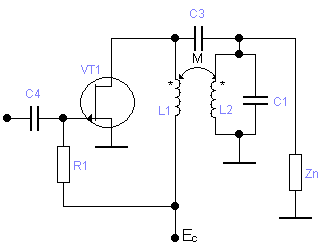Объясним назначение каждого из элементов схемы представленной на рисунке 1.
Рисунок 1- Исходная схема
Назначение элементов схемы: резистор R1 определяет положение рабочей точки транзистора; С3 – разделительный конденсатор; элементы L1, L2,С1, образуют резонансный контур высокой добротности; Zn=Rn+jXn – сопротивление нагрузки.
Данная схема является резонансным усилителем.
Определим резонансную частоту контура fr:
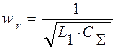
где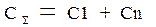 
;
=2.3224e+006 рад/с
|
|
|
Так как
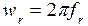
Тогда получаем, что:
3.6963e+005 Гц
Для оценки усилительных свойств транзистора вводится понятие граничной частоты по крутизне и обозначается как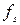 
.
На этой частоте модуль крутизны уменьшается в 1,4 раза по сравнению низкой частотным значением, граничная частота определяется по формуле 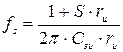1:
, (1)
где 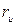- параметр, который характеризует сопротивление участка канала полевого транзистора вблизи стока и стока.
Рассчитаем по формуле 1 граничную частоту
,
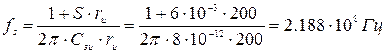Для упрощения анализа схемы определим значение сопротивления вспомогательных элементов на частоте равной резонансной частоте. К таким элементам относятся:
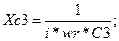
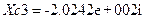
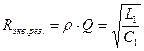
К таким элементам относиться конденсаторы С4,С3 и резистор R1. Для fp =3.64 МГц, Xc4=0.39Ом R1=150к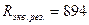Ом
Ом
r = wr*L2/Q - сопротивление потерь в резонансном контуре.
2. Параметры линейной схемы замещения транзистора на резонансной частоте контура
Рассчитаем малосигнальные параметры транзистора используя расчетное значение резонансной частоты. Транзистор будет охарактеризован четырьмя комплексными параметрами. У - параметры для схемы с общим истоком определяются соотношениями:
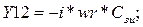
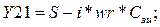
В результате получаем значения в См:
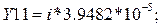
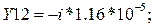
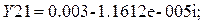
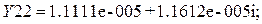
По полученным значениям строим неопределенную матрицу проводимости:
Y=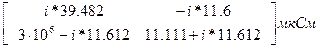 
При использовании в анализе метода контурных токов нам потребуются параметры Zij, которые получаем из Yij-параметров с помощью формул пересчёта:
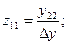
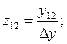
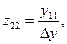(3)
где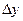 
-- определитель матрицы Y.
В результате получаем неопределённую матрицу сопротивлений со следующими элементами в Омах:
Z11=326.27 - 317.98i
Z12=-329.16 + 3.0198i
Z21=-1109.3 - 85035i
Z22=1119.1 - 10.267i
Построение эквивалентной схемы заданной цепи для рабочего диапазона частот
Так как резонансная частота fr много меньше граничной частоты fs можем использовать схему замещения.
С учетом того, что транзистор работает в узкополосном режиме вблизи резонансной частоты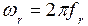 
эквивалентную схему транзистора целесообразно преобразовать в следующий вид представленный на
|
|
|
рисунке 2.
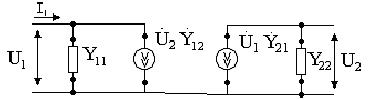
Рисунок 2 - Схема замещения
В результате данного преобразования проводимости ветвей будут комплексными, но не будут зависеть от частоты.
Для заданной схемы перейдем от параметров виде Y-параметров к Z- параметрам. Для этого, необходимо преобразовать матрицу Y-параметров, используя формулы 3. Результат представлен на рисунке 3.
Рисунок3-Эквивалентная схема 2.
Таким образом, схема примет вид, представленный на следующем рис.4
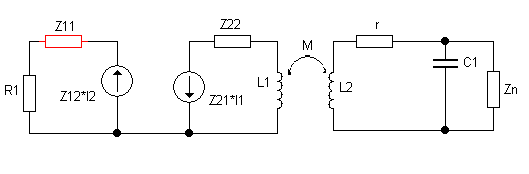
рисунок 4-схема замещения
Пересчитаем параллельное соединение C1, Cn и Rn в последовательное соединение.
Zn`=1/(1/Rn+i*wr*C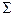 
),
Где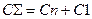 
 |
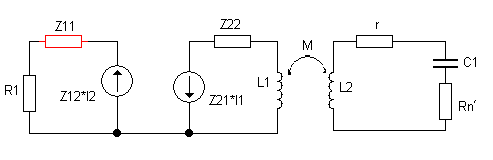
Рисунок 5-схема замещения для заданного диапазона частот
4.Нахождение передаточной функции цепи по напряжению. Построение АЧХ и ФЧХ схемы для рабочего диапазона частот.
Для нахождения передаточной функции используем метод контурных токов. В результате преобразования схемы мы получили контура. Схема представлена на рис.!!!.
Вычисления будем проводить используя программу MatLab.
Составим систему уравнений связи напряжений и контурных токов.
Матрица напряжений Е имеет следующий вид:
E = 1
Матрица сопротивлений Z задается следующим образом:
Z=[ Z11+R1 Z21 0
Z12 Z22+i*wr*L1 -i*wr*M
0 -i*wr*M Rn1+r*(1+Q*(f/fr-fr/f)) ];
Заменяя третий столбец матрицы Z, матрицей Е получим матрицу U:
U=[ Z11+R1 Z21 1
Z12 Z22+i*wr*L1 0
0 -i*wr*M 0 ];
Контурные токи находятся из формулы:
I = Z-1*E,
Передаточная функция по напряжению есть отношение напряжения на входе к напряжению на выходе, то есть К= 
. Значит, передаточная функция данной схемы с учетом того, что Uвх = 1, имеет следующий вид:
K=Zn`*(det(U)/det(Z)),
где det(U) и det(Z) детерминанты матриц U и Z соответственно.
АЧХ схемы представлен на рисунке!!, ФЧХ – рисунке!!.
Рисунок 6 – АЧХ схемы
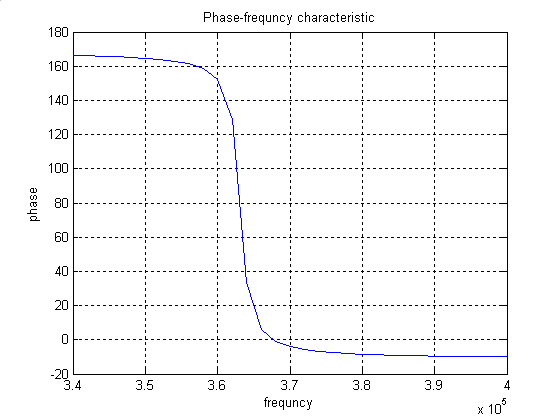
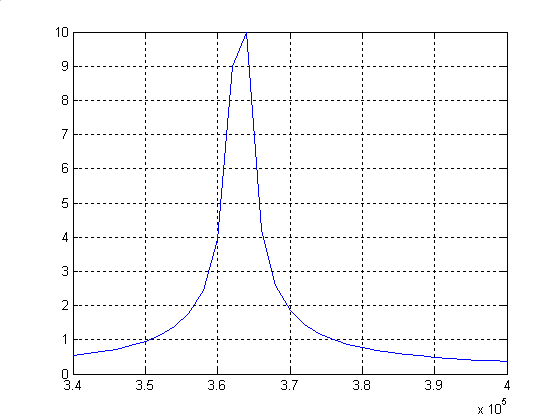
Рисунок 7 – ФЧХ схемы
6. Импульсная характеристика цепи.
Импульсную характеристику схемы будем строить исходя из реакции схемы на подачу на её вход одиночного прямоугольного импульса. Реакция схемы на такое воздействие является импульсная характеристика.
|
|
|
Входной сигнал представлен на рисунке 11.
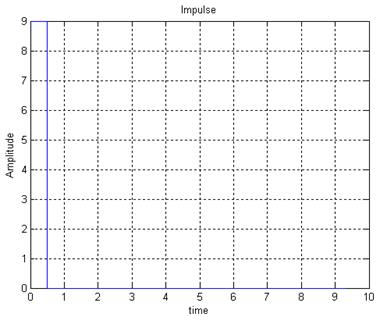
Рисунок 11 – импульс прямоугольной формы
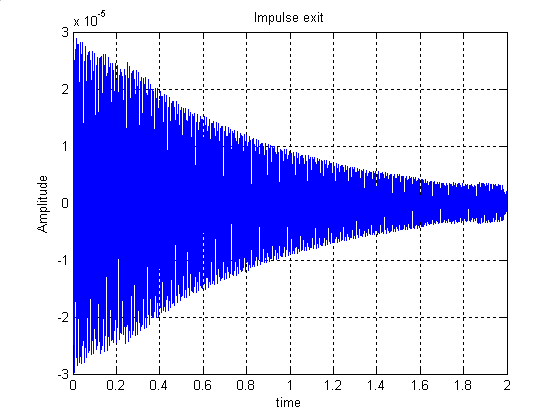
Рисунок 12- импульсная характеристика
5. АЧ и ФЧ спектры управляющего сигнала
Данный в условии управляющий сигнал представлен формулой вида:
s=9*(exp(-1000*t)-exp(-10000*t));
где t – время.
Пускай в схему поступает 1 период управляющего сигнала (рисунок!)
АЧ и ФЧ спектры управляющего сигнала на входе представлены на рисунках 9 и 10 соответственно.
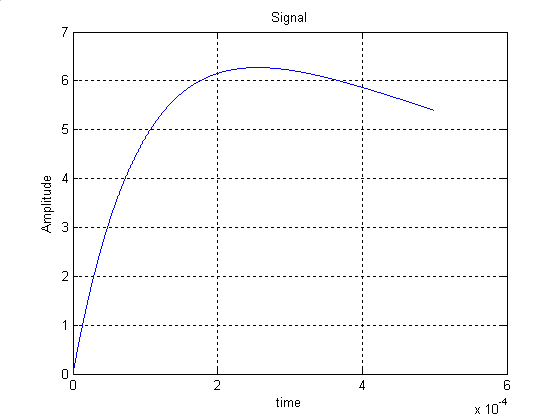
рисунок 8- управляющий сигнал
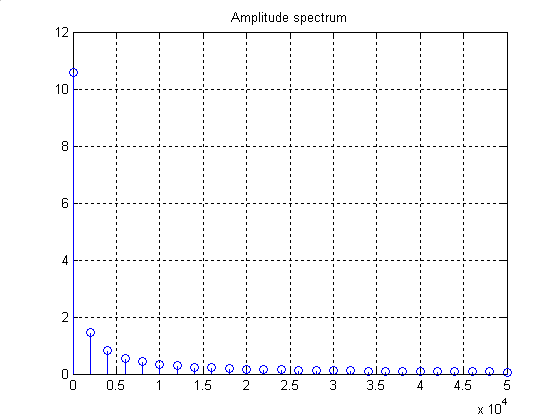
Рисунок 9 – АЧ спектр управляющего сигнала на входе
Рисунок 10 – ФЧ спектр управляющего сигнала на входе
7. Амплитудно-модулированное колебание. Его АЧ и ФЧ спектры
По условию дано:
модуляция – балансовая,
Uмах = 0.2 В,
начальная фаза несущей частоты равна 0 рад.
Амплитудно-модулированное колебание задается формулой:
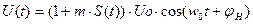,[3]
где по условию m=1
U0 = 0.2 В;
φH = 0 рад.
Значит, аналитическое выражение амплитудно-модулированного сигнала с модуляцией по закону заданного управляющего сигнала будет выглядеть следующим образом
;
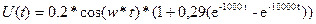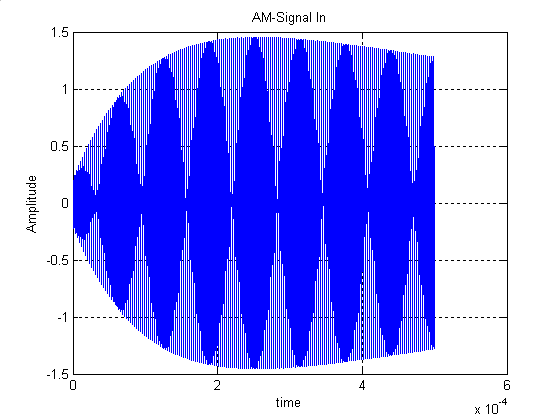График U(t) представлен на рисунке 11.
Рисунок 13- амплитудно-модулированное колебание
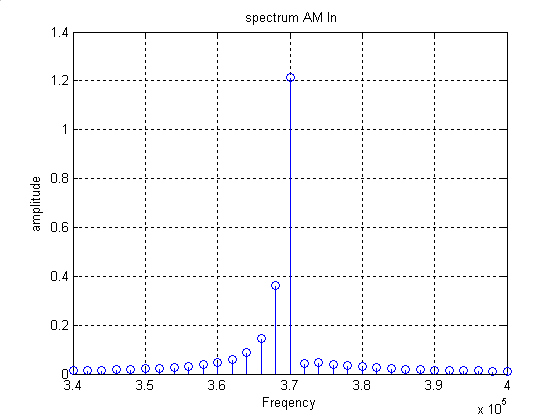
На рисунках 14 и 15 представлены амплитудный и фазовый спектры амплитудно-модулированного колебания соответственно.
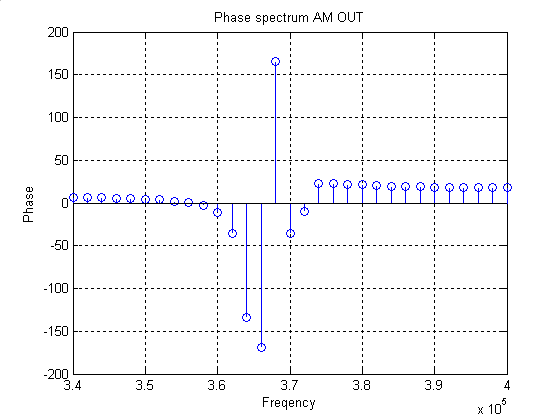Рисунок 14 – АЧ спектр амплитудно-модулированного колебания
Рисунок 15 – ФЧ спектр амплитудно-модулированного колебания
Функция спектральной плотности[3] имеет вид:
8.Отклик схемы при воздействии на её вход АМ - сигнала
Пусть на вход данной схемы подается сигнал, который представлен на рисунке 8. Для нахождения сигнала на выходе схемы надо поэлементно перемножить спектр АМ сигнала на АЧХ схемы, а затем, применив обратное преобразование Фурье, получить сигнал на выходе. АЧ и ФЧ спектры сигнала на выходе представлены на рисунках 16 и 17 соответственно. АМ сигнал на выходе представлен на рисунке 18.
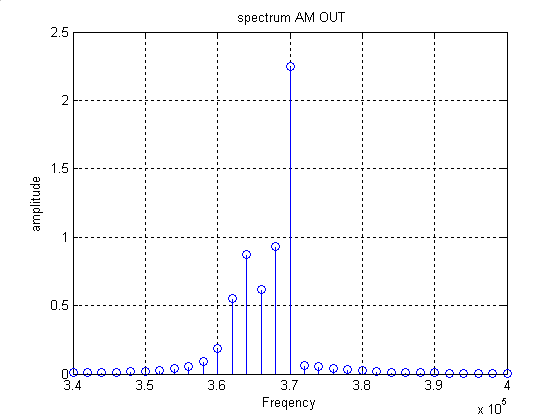
Рисунок 16 – АЧ спектр АМ сигнала на выходе
|
|
|
Рисунок 17 – ФЧ спектр АМ сигнала на выходе
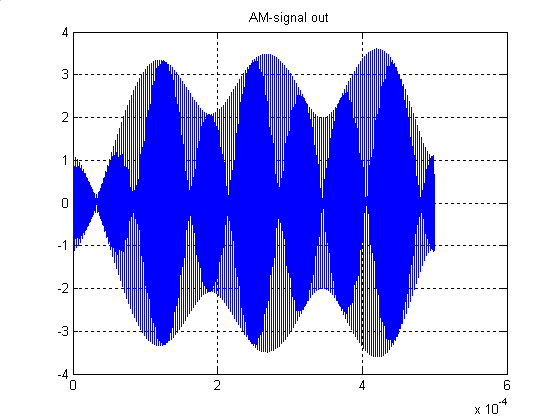
Рисунок 18 – АМ сигнал на выходе
9.Выводы.
В ходе данной работы были выполнены следующие задачи:
1. Объяснили назначение всех элементов схемы: резистор R1 определяет положение рабочей точки транзистора; С3 – разделительный конденсатор; элементы L1, L2,С1, образуют резонансный контур высокой добротности; Zn=Rn+jXn – сопротивление нагрузки.
2. Определили параметры линейной схемы на резонансной частоте,fr=3.6963e+005 Гц изобразили эквивалентную схему[рис.3] заданной цепи для рабочего диапазона частот;
3.Построили АЧХ, ФЧХ.Представлены на рис.6 и рис.7.
4.Построили АЧ и ФЧ спектры управляющего сигнала заданного выражением s=9*(exp(-1000*t)-exp(-10000*t)).
Построили АМ-сигнал с модуляцией по закону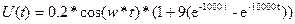 
.
Функция спектральной плотности сигнала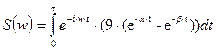 
Построили АЧ-спектр, ФЧ-спектр представленные на рис.14,рис.15.
5.Импульснуя характеристика цепи представлена на рис12.
6.Построили отклик схемы при воздействии на ее вход АМ-сигнала.
Выходной сигнал представлен на рис.18. Схема искажает сигнал. Полоса пропускания резонансного усилителя уже чем диапазон частот спектра сигнала. Чтобы использовать резонансный усилитель для усиления заданного сигнала s=9*(exp(-1000*t)-exp(-10000*t)) необходимо увеличить полосу пропускания усилителя. Для этого необходимо вносить изменение в схему усилителя, изменять добротность контура.
Вывод:
Резонансный усилитель представленный на рисунке1 не пригоден для
Усиления заданного сигнала s=9*(exp(-1000*t)-exp(-10000*t))
Все расчеты данной работы были выполнены в среде MatLab. Данная среда разработки была выбрана из-за наличия в ней специального пакета программ обработки сигналов. Данный пакет значительно упрощает расчет параметров схемы и ее характеристик
10. Список литературы
|
|
|
