Электропривод с двигателем постоянного тока с независимым возбуждением.

 

Двигатели постоянного тока (ДПТ) широко применяются в промышленных, транспортных и других установках, где необходимо плавное регулирование скорости вращения (прокатные станы, металлорежущие станки, электрическая тяга на транспорте и. т. п.). В зависимости от способа электромагнитного возбуждения ДПТ подразделяют на ДПТ с независимым, последовательным и смешанным возбуждением. Иногда встречается название ДПТ с параллельным возбуждением, но необходимо учесть, что такой ДПТ является частным случаем ДПТ с НВ и этот термин применяется как доопределяющий.

Схема включения ДПТ с независимым возбуждением (ДПТ с НВ) приведена на рис. 2.1. Для ДПТ с НВ справедлива система уравнений, описывающая его статическое состояние:

 

U=IR+E

Е=с ; (1.1)

М=сI;

где U - напряжение на якорной цепи, В; R - суммарная сопротивление якорной цепи, Ом; М - электромагнитный момент, Нм; I -ток якоря, А; - угловая скорость двигателя, рад/с; Е - ЭДС вращения якоря, В; с = кФ - коэффициент пропорциональности, Вс; к = pN/2na - постоянная ДПТ (р - число пар полюсов; N - число активных проводников якорной обмотки; а - число пар параллельных ветвей якорной обмотки) Ф - магнитный поток, Вб.

Решая первые два уравнения в системе (1.1) относительно Е, можно получить известное уравнение электромеханической характеристики ДПТ

 

, (1.2)

 

которое определяет зависимость = f(I).

С учетом третьего уравнения в (1.1) уравнение (1.2) можно переписать в виде зависимости w=f(M) которая определяет механическую характеристику ДПТ:

 

, (1.3)

 

Или

 

(1.4)

 

 

Рисунок 1.1 - Схема включения ДПТ с НВ

 

которое определяет зависимость = f(I).

Данное уравнение механической характеристики определяет зависимость скорости вращения от момента на валу двигателя, т.к. в статике вращающий момент равен моменту сопротивления Мс на валу ДПТ, то это уравнение определяет зависимость от Мс, прикладываемого к валу.

Стоит сказать, что здесь мы оперируем величиной электромагнитного момента М, который превышает выходной момент на валу на величину, соответствующую потерям в стали и механическим потерям от трения, но в большинстве практических расчетов можно считать, что эти моменты равны. Коэффициент пропорциональности с = кФ можно считать постоянным для тех ДПТ с НВ, у которых имеются компенсационные обмотки или в случае, когда можно пренебречь влиянием реакции якоря на величину Ф. Вообще-то влияние поперечной реакции якоря на Ф ведет к нарушению линейности механической характеристики по мере увеличения тока.

Из анализа уравнения электромеханической характеристики (формула 1.2) видно, что она может быть представлена прямой линией (рис. 1.2) при неизменных напряжении U, магнитном потоке Ф, создаваемом ОВ и сопротивлением якорной цепи R. Если U = U_ном, Ф = Ф_ном и R_д = 0, электромеханическая характеристика называется естественной. При изменении хотя бы одного из указанных параметров электромеханическая характеристика называется искусственной. Таким образом, можно отметить, что ДПТ с НВ обладает лишь одной естественной характеристикой и множеством искусственных.

Нетрудно видеть, что в случае, если I=0, имеет место режим идеального холостого хода и при этом = = U/кФ == U/c, т.е. и .

С увеличением нагрузки на валу ДПТ возрастает и ток якоря I, т.к. М == сI, а это в свою очередь ведет к падению . В случае, если = 0, то при подведенном к якорю напряжении имеет место режим короткого замыкания, при котором из уравнения (1.2) следует, что I_кз = U/R. Максимальное значение тока короткого замыкания имеет место при R_д = 0, когда R = R_я (R_я - собственное сопротивление обмотки якоря), и оно может в десятки раз превышать величину I_н двигателя, т.к. I_я величина достаточно малая. Реально режим короткого замыкания имеет место, кратковременно, при пуске двигателя и при стопорении двигателя моментом сопротивления.

 

Рисунок 1.2 - Механическая и электромеханическая характеристики ДПТ с НВ

 

При прямом пуске двигателя ударные значения тока I_кз>>I_н, поэтому якорная обмотка может быстро перегреться и выйти из строя, кроме того, большие токи негативно влияют и на работоспособность щеточно-коллекторного узла. Cказанное обуславливает необходимость ограниченияI_кз до какой-либо приемлемой величины, либо введением дополнительного сопротивления в якорную цепь R_д, либо уменьшением питающего напряжения U. Величина максимально допустимого тока определяется коэффициентом перегрузки по току К_т, обычно принимающим значения от 2 до 5, в зависимости от типа двигателя. Максимально допустимый ток короткого замыкания должен соответствовать неравенству:

 

. (1.5)

 

Для микродвигателей обычно осуществляется прямой пуск без добавочных сопротивлений, но с ростом габаритов ДПТ необходимо производить реостатный пуск, особенно если привод с ДПТ используется в напряженных режимах с частыми пусками и торможениями. Практически надо помнить, что только частыми пусками можно «сжечь» ДПТ, если конечно не ограничивать пусковые токи. С введением R_д в цепь якоря жесткость электромеханической характеристики уменьшается, что и видно из рисунка 1.2.

Из выражения (1.4) следует, что графически механическая характеристика ДПТ с НВ может быть представлена прямой линией с двумя характерными точками - скоростью холостого хода w_о и моментом короткого замыкания М_кз, который также называется пусковым. Величина М_кз определяется как М_кз = сI_кз = кФU/R. С введением добавочного сопротивления R_д в цепь якоря жесткость механических характеристик также падает, что с успехом используется при регулировании скорости вращения.

Уравнения механической характеристики можно переписать в виде:

 

, (1.6)

 

где = MR/ (кФ) = MR/c - перепад скорости, a R = R_я + R_д.

С учетом пропорциональной связи между I и М следует, что график механической и электромеханической характеристик один и тот - же при соответствующем масштабировании по оси абсцисс величин I и М, поэтому часто обозначение по оси абсцисс приводится как М (I).

Из уравнения механической характеристики (1.4) следует, что принципиально может регулироваться изменением напряжения U, магнитного потока Ф, создаваемого ОВ, и сопротивления якорной цепи R.

Одним из основных показателей, характеризующих способы регулирования скорости является диапазон регулирования D, который в электроприводе определяется как отношение максимальной скорости вращения _max к минимальной _min

 

D = . (1.7)

 

Как правило, диапазон регулирования представляют в числах в виде соотношения, например100:1 и т.д. Естественно, диапазон регулирования увязывается с требуемой стабильностью скорости при заданном отклонении момента.

Как следует из выражения (1.4), при изменении питающего напряжения можно получить семейство параллельных механических характеристик (рис. 1.3).

Практически имеется возможность только уменьшать напряжение питания якоря относительно его номинального значения U_н, т.е. при регулировании скорости изменением U должно выполнятся неравенство:

 

U U_н, (1.8)

 

при этом скорость вращения можно регулировать только вниз от основной, соответствующей естественной характеристике. Это обусловлено тем, что уже на стадии своего проектирования ДПТ рассчитывается на конкретное номинальное напряжение, и превышение которого может привести к пробою изоляции. Напряжение на якоре может регулироваться различными электромашинными и статическими устройствами.

w

Рисунок 1.3 - Механические характеристики ДПТ с НВ при различных напряжениях на якоре U_ном>U₁>U₂

 

Из уравнения механической характеристики (1.4) следует, что, например, при постоянном моменте сопротивления М_с на валу можно получить различные установившиеся угловые скорости ниже основной введением в цепь якоря добавочного сопротивления (рис. 1.1). Жесткость механических характеристик уменьшается с увеличением величины добавочного сопротивления R_д. Диапазон регулирования скорости практически не превышает 2:1. Способ характеризуется большими тепловыми потерями на добавочном сопротивлении R_д.

При введении добавочного сопротивления R_в в цепь обмотки возбуждения можно изменять величину магнитного потока двигателя Ф в сторону уменьшения от его номинального значения Ф_н, которое достигается при R_в = 0.

Как нетрудно видеть из уравнения электромеханической характеристики (1.2), для различных значений потока Ф можно получить семейство электромеханических характеристик, представленное на рис. 1.4.

Угловая скорость идеального холостого хода w₀ определяется следующим выражением: . На рис. 1.4 нижняя характеристика соответствует номинальному потоку возбуждения Ф_н. Если при этом добавочное сопротивление в якорной цепи R_д равно 0 и якорь запитывается номинальным напряжением U_н,то эта характеристика будет естественной. При уменьшении величины потока возбуждения угловые скорости вращения холостого хода возрастают. Ток короткого замыкания при этом остается неизменным.

Момент ДПТ определяется выражением (1.1), поэтому с уменьшением величины потока возбуждения Ф уменьшается и соответствующий пусковой момент М_кз. На рис. 1.5 представлены механические характеристики для различных значений потоков. Практически этот способ используется только для регулирования угловой скорости вращения вверх от основной. Экономически целесообразно регулировать угловую скорость вращения при токе якоря равном номинальному, но при этом номинальные значения моментов будут различными для различных значений величины потока Ф. Точки, соответствующие номинальным моментам двигателя будут лежать на гиперболической кривой, обозначенной пунктирной линией на рис. 1.5.

Рисунок 1.4 - Характеристики ДПТ с НВ при изменении магнитного потока .

 

w

Из этого следует, что целесообразная при таком способе регулирования нагрузка должна характеризоваться нелинейно спадающей механической характеристикой. Диапазон регулирования для двигателей специального исполнения может достигать10:1, но обычно составляет2:1.

Рисунок 1.5 - Характеристики ДПТ с НВ при изменении магнитного потока .

 

Согласно принципу обратимости двигатель может работать помимо двигательного и в генераторных режимах. Генераторный режим работы электродвигателя относятся к торможению электродвигателя. Различают следующие генераторные (тормозные) режимы:

• торможение с отдачей энергии в сеть (рекуперативное);

• динамическое торможение;

• торможение противовключением.

Если сторонним устройством разогнать ДПТ с НВ до скорости выше скорости холостого хода, то он начинает работать генератором, включенным параллельно с сетью, отдавая ей электрическую энергию. Ток якоря при этом изменяет свой знак, т.к. Е > U и ДПТ переходит в тормозной режим с моментом М_т = - М.

В этом случае уравнение механической характеристики может быть представлено как

 

= U/c + M_тR/c ² (1.9)

 

 

Нетрудно видеть, что графически зависимость == f(M_т) в данном случае является продолжением механической характеристики двигательного режима и изображается во 2 или 4 квадратах (рис. 1.6). Данный тормозной режим весьма экономичный и широко применяется в промышленности и на транспорте при некоторых способах регулирования скорости, например при регулировании скорости вращения изменением питающего напряжения U.

 

Рисунок 1.6 - Механические характеристики ДПТ в режиме рекуперативного торможения (R_д2>R_д1).

 

Но данный режим работы ДПТ может применяться только при работе электродвигателя на скоростях больших скорости идеального холостого хода w₀.

При работе ДПТ с НВ в режиме генератора независимо от сети или в режиме динамического торможения якорную цепь электродвигателя отключают от сети и замыкают её на тормозное сопротивление (рис. 1.7).

Уравнение механической характеристики для этого режима запишется как

 

=М_тR/с² (1.10)

 

где М_т - тормозной момент, R - сопротивление якорной цепи. R = R_я + R_p.

Ток якоря можно определить как

 

I=-E/R, (1.11)

 

т.е. он изменяет свой знак, чем и обуславливается процесс торможение.

Способ динамического торможения достаточно экономичный, т.к. двигатель работает генератором на постоянную нагрузку, потребляя из сети энергию только на электромагнитное возбуждение. При переводе ДПТ из двигательного режима в режим динамического торможения ограничивают величину максимального тормозного тока в момент переключения.

Режим генератора последовательно с сетью или режим торможения противовключением имеет место тогда, когда обмотки двигателя включены для вращения в одну сторону, но под действием внешнего момента или сил инерции ротор вращается в противоположную сторону.

При превышении активным моментом сопротивления величины пускового момента имеет место тормозной спуск, что приводит к изменению направления вращения якоря двигателя и соответственно знака ЕДС. Из первого уравнения системы (1.1) следует, что в этом случае ток якоря определяется как I=(U+E)/R, т.е. ток якоря превышает значения токов короткого замыкания.

 

Рисунок 1.7 - Схема включения ДПТ в режиме динамического торможения.

На рис. 1.8 представлены механические характеристики режима динамического торможения.

 

Рисунок 1.8 - Характеристики динамического торможения ДПТ с НВ.

 

Поэтому для реализации этого режима необходимо ограничивать ток якоря введением добавочного сопротивления R_д. Графически механические и электромеханические характеристики в этом случае являются продолжением соответствующих характеристик в 4 квадрант (рис. 1.9).

Если у ДПТ, работающего в двигательном режиме изменить полярность напряжения на обмотке якоря на противоположную, то знак тока якоря I изменится на противоположный в соответствии с выражением I=-(U+E)/R. Двигатель переходит в тормозной режим, и его механическая характеристика изображается во 2 квадранте. При этом происходит интенсивное торможение и скорость вращения двигателя падает до нуля. Если в этот момент времени обмотку якоря не отключить от сети, то направление вращения изменится на противоположное, т.е. двигатель реверсируется. С энергетической точки зрения данный способ не экономичен, т.к. большое количество энергии выделяется на добавочном сопротивлении, которое необходимо включать в якорную цепь для ограничения бросков тормозного тока. Механические характеристики для этого режима торможения представлены на рис. 1.10.

Рисунок 1.9 - Характеристики ДЛТ с НВ в режиме тормозного спуска.

 

Режим тормозного спуска широко применяется в грузоподъемных механизмах для опускания грузов.

 

w

Рисунок 1.10 - Характеристики ДПТ с НВ в режиме торможения противовключением при изменении полярности питающего напряжения (R₃>R₂>R₁).

 

Переходные процессы. Неустановившиеся или переходные процессы, имеющие место при переходе привода из одного установившегося состояния в другое, совершающемся во времени. При этом

 

(1.12)

 

Можно назвать следующие причины возникновения переходных процессов:

Изменение момента сопротивления М_с;

изменение момента на алу двигателя М, то есть переход привода с одной характеристики на другую, имеющий место при пуске, торможении, реверсе, регулировании скорости, изменении какого-либо параметра привода.

Необходимость в изучении переходных процессов возникает в связи с тем, что производительность ряда ответственных механизмов (например, реверсивного прокатного стана) определяется быстротой протекания переходных процессов; качество выполнения многих технологических операций определяется переходными процессами (движение лифта, врезание резца в деталь и т.п.); механические и электрические перегрузки оборудования в большинстве случаев определяются переходными процессами. Основная задача при изучении переходных процессов сводится к определению зависимостей w(t), M(t) и i(t) для любых конкретных приводов в любых условиях.

Мгновенный наброс и сброс нагрузки, пуск, реверс, торможение – вот круг задач которые приходится решать при исследовании переходных режимов. При этом основным фактором, влияющим на переходной процесс, является механический момент инерции (J). Такие электрические параметры, как индуктивность обмоток якоря, индуктивность обмоток возбуждения и т. п., оказывают ничтожно малое влияние на работу электродвигателя в переходных режимах, поэтому при исследовании переходных процессов ими обычно пренебрегают. Фактор, вызывающий переходный процесс, изменяется скачкообразно (мгновенно) то есть много быстрее, чем скорость.

Все переходные процессы подчиняются, очевидно, механическому уравнению движения

(1.13)

 

Искомые зависимости w(t) и M(t) должны быть получены путем решения этого уравнения при заданных начальных условиях. Конкретные особенности привода отразятся в виде зависимостей M(w) и M_с (w) входящих в уравнение.

Рассмотрим поведение привода при следующих условиях:

1. M = const, M_с = const

а) б)

Рисунок 1.11 - Механические характеристики (а) и временные зависимости (б) при М = const и M_c = const

 

Пусть привод работал в точке w _нач, М _нач = М _с (рис. 1.11) некоторой характеристики (она нас не интересует) и в момент времени t = 0 был мгновенном переведен на новую характеристику, показанную на рис. 1.11, а жирной линией.

Уравнение движения привода в переходных режимах (1.13) в этом случае представляет собой дифференциальное уравнение с разделяющимися переменными и его решение имеет вид:

 

(1.14)

 

 

Постоянную интегрирования С найдем из начального условия - при t = 0, w = w _нач: w _нач = С.

Окончательно будем иметь:

 

(1.15)

 

Это решение действует на интервале w _нач < w < w _кон, так как по условию при w = w _кон функция w(М) терпит излом. На этом интервале М =М₁.

Графики переходного процесса приведены на рис. 1.11,б. При этом время переходного процесса t _пп:

 

(1.16)

 

Рассмотренный простейший случай имеет очень большое практическое значение, так как к нему может быть сведено в целях оценки времени и характера переходного процесса большое число конкретных задач.

2. М_с = const, M линейно зависит от w, b < 0.

Пусть характеристики двигателя и механизма имеют вид, представленный на рис. 1.12. Уравнение линейной механической характеристики двигателя с отрицательной жесткостью может быть записано как

Рисунок 1.12 - Механические характеристики и графики переходных процессов w(t) и M(t) при линейной зависимости w(М)

 

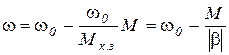(1.17)

или

(1.18)

 

где - жесткость механической характеристики; для линейной характеристики .

Подставив полученное уравнение в уравнение движения привода, после простых преобразований получим:

 

(1.19)

 

Выражение в правой части представляет собою w _кон. Обозначив коэффициент перед производной через Т _м, запишем:

 

(1.20)

 

Теперь подставим в уравнение движения (1.13) вместо выражение и получим

 

(1.21)

 

Итак, мы обнаружили, что в рассматриваемом переходном процессе, как для скорости, так и для момента справедливо одинаковое уравнение вида

 

, (1.22)

 

то есть линейное неоднородное дифференциальное уравнение с постоянной правой частью.

Коэффициент при производной

 

(1.23)

 

называют электромеханической постоянной времени.

Рисунок 1.13 - определение электромеханической постоянной времени Т_м

 

Для выяснения смысла этой величины рассмотрим условный привод с характеристикой, показанной на рис. 1.13. Определив время разгона такого привода

 

(1.24)

 

замечаем, что оно выражается так же, как Т _м. В связи с этим можно считать, что электромеханическая постоянная времени Т _м представляет собою время, за которое привод разогнался бы вхолостую до w = w₀ под действием момента короткого замыкания.

2 Практическая часть

 

В данной части курсового проекта мы будем строить систему управления точного позиционирования скользящей части стола металлообрабатывающего станка

2.1 Построение структурной схемы АЭП

 

Данная структурная схема имеет вид:

 

Рисунок 2.1 – структурная схема электропривода.

 

Схема состоит из следующих элементов:

­ панель управления;

­ ПД-регулятор;

­ ДПТ;

­ редуктор;

­ стол;

­ обратная связь по току с отсечкой;

­ Функциональная часть;

­ датчик линейного перемещения.

Далее приведено описание работы системы

С панели управления сигнал поступает на функциональную часть, которая, в свою очередь, регулирует работу ДПТ для необходимого нам состояния. Система оснащена двумя обратными связями, которые измеряют и подают на функциональную часть значения. Вся система работает на напряжении 110 В, поэтому в ней отсутствуют усилители и преобразователи.

Рассмотрим все части системы в отдельности:

Панель управления. На панели управления находятся кнопки включения и выключения.

Функциональная часть. Она включает в себя сумматор и ПД-ругелятор. ПД-регулятор мы используем из-за того, что стол описывается реально-интегрирующим звеном. Сумматор работает как сравнивающий элемент, он сравнивает значения, которые поступают с обратных связей с задающим воздействием и выдает сигнал ошибки.

Обратные связи:

1. Обратная связь по току включает в себя амперметр и звено нечувствительности, для использования тока с отсечкой.

2. Обратная связь, которая контролирует положение стола будет оснащена реостатным датчиком, так как он более точный и позволяет измерить отрицательное перемещение.

Редуктор. Позволяет преобразовать угловое перемещение в линейное перемещение.

Двигатель постоянного тока – 4ПО100L1 работает на напряжении 110 В, поэтому в схеме отсутствуют преобразователи и усилители.

Стол является исполнительным механизмом нашей системы.

 

2.2 Синтез математической модели объекта

 

Проанализировав нашу систему с ее объектом управления, мы пришли к выводу, что входным воздействием является момент на двигатель M_д(t), а в роли выходной величины выступает перемещение рейки x(t).

 

∑F(t)=ma(t) (2.1)

 

где ;

;

F_g(t) – сила, развиваемая двигателем, ;

- сила трения, ;

- момент двигателя;

- радиус барабана, м;

- коэффициент трения, .

Преобразуем нашу формулу по Лапласу и найдем передаточную функцию.

 

(2.2)

 

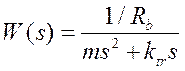(2.3)

 

 

2.3 Расчет параметров ДПТ

 

Сопротивление обмотки якоря определяется по закону Ома для участка цепи:

 

(2.4)

 

(Ом)

 

Индуктивность обмотки якоря:

 

(2.5)

 

(Гн)

 

Индуктивность обмотки возбуждения:

 

(2.6)

 

(Гн)

 

Взаимная индуктивность между цепью якоря и цепью обмотки возбуждения:

 

(2.7)

 

(Гн)

 

Потери мощности ДПТ складываются из механических потерь и электромагнитных потерь.

Механические потери определяются от номинальной мощности ДПТ:

 

(2.8)

 

(Вт)

 

Коэффициент вязкого трения:

 

(2.9)

 

Коэффициент сухого трения:

(2.10)

 

2.4 Построение в MatLab релейной схемы управления

 

Рисунок 2.2 – релейная схема управления электроприводом

Были подобраны резисторы R₁=10 Ом, R₂=5 Ом, R₃=1 Ом.

Промоделировав полученную схему, мы получили:

Рисунок 2.3 – угловая скорость вращения ротора

Двигатель разгоняется до скорости 10 рад/сек за четыре этапа, время регулирования t=30.5с.

 

Рисунок 2.4 – ток якоря

Пусковой ток достигает значения 4.7 А.

Рисунок 2.5 – график переходного процесса электропривода

 

 

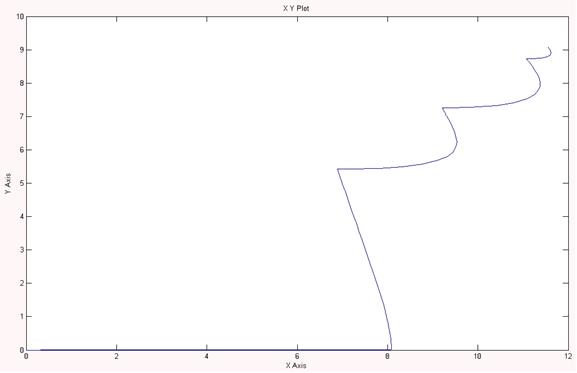
Рисунок 2.6 – механическая характеристика ДПТ

 

Рисунок 2.7 – механическая характеристика электропривода

2.5 Построение в MatLab схемы управления с регулированием по скорости

 

Рисунок 2.8 – схема управления электроприводом по скорости

 

Промоделировав полученную схему, мы получили:

Рисунок 2.9 – угловая скорость вращения ротора

Двигатель разгоняется до скорости 10.54 рад/сек. Время регулирования t=0.7с.

Рисунок 2.10 – ток якоря

Ток якоря достигает установившегося значения 5.46 А

 

Рисунок 2.11 – график переходного процесса электропривода.

Рисунок 2.12 – механическая характеристика ДПТ

 

Рисунок 2.13 – механическая характеристика электропривода

 

2.6 Построение в MatLab схемы управления с ПД-регулятором

 

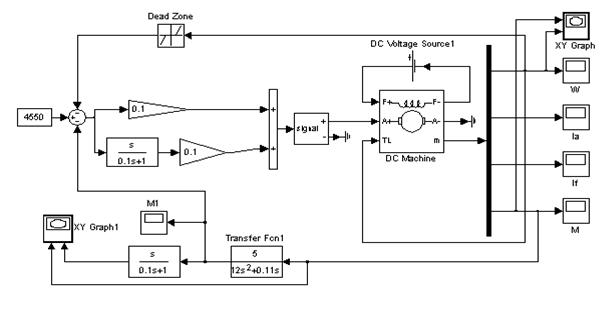
Рисунок 2.14 – схема управления электроприводом при помощи ПД-регулятора

Промоделировав полученную схему, мы получили:

Рисунок 2.15 – угловая скорость вращения ротора

Двигатель с ПД-регулятором разгоняется до скорости 9·10^-3 рад/сек за 1.5 секунды.

Рисунок 2.16 – ток якоря

Значение тока якоря составляет 0.45 А.

Рисунок 2.17 – график переходного процесса электропривода

Переходный процесс достигает установившегося режима за 25 секунд.

Рисунок 2.18 – механическая характеристика ДПТ

 

Рисунок 2.19 – механическая характеристика электропривода

 

2.7 Сравнительный анализ разработанных систем управления

 

Критерий	Релейная система	Регулирование по скорости	ПД-регулятор
Скорость вращения ротора, С-1			9·10-3
Ток якоря, А	4.7	5.46	0.45
Время регулирования, с	30.5	0.5	1.5

 

Для выбора наиболее оптимальной схемы мы должны сравнить все параметры и определить наиболее подходящую. Так, например, пусковые токи в первой и второй схемах примерно равны – 4.7 А и 5.46 А соответственно, а в третьей схеме он равен 0.45 А, хотя мы поставили для уменьшения пускового тока звено нечувствительности, но уменьшать ток еще больше не рационально.

Проанализировав все результаты, я решил, что схема пуска двигателя по скорости является наиболее оптимальной, для нашей системы.
Хотя она и обладает относительно большим пусковым током 5.46 А, зато в ней самое маленькое время регулирования 0.5 с.

Выводы

 

В данном курсовом проекте я разработал систему автоматического управления электроприводом точного позиционирования скользящей части стола металлообрабатывающего станка с двигателем постоянного тока. Были разработано три системы управления: релейная система, система регулирования по скорости и система регулирования с ПД-регулятором. Также были построены в среде Simulink имитационные модели для каждой из систем. После моделирования я получил графики выходных характеристик электропривода и по этим данным сделал анализ систем и выбрал лучшую.

Для регулирования электропривода наиболее выгодно использовать регулирование по скорости, так как этот вид регулирования обладает самыми оптимальными для нашей системы характеристиками.

Список использованных источников и литературы

 

1. Дементьев Ю.Н., Чернышев А.Ю., Чернышев И.А. «Автоматизированный электропривод: Учебное пособие» – Томск: Изд-во ТПУ, 2009. – 224 с.

2. http://freepapers.ru

3. http://energo20.ru

4. О. О. Осьмачко «Лабораторный практикум по дисциплине «Автоматизированный электропривод» - Харьков: ХНАДУ, 2008.-40 с.

5. Конспект лекций по дисциплине «Автоматизированный электропривод».

Поделиться:

Воспользуйтесь поиском по сайту: