 |
Прямая линия и её уравнения
|
|
|
|
Раздел № 1 (Базовый, максимальная оценка – «удовлетворительно»)
Векторы на плоскости и в пространстве.
1. Дано: 
. Найти: 
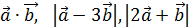
2. Найти модуль равнодействующей 
двух сил 
и 
и углы образуемые равнодействующей с силами и 
, , если | | = 4H | 
| = 6H, а (
) = 60°
3. Дан тетраэдр ABCD. Найдите сумму векторов: 
+ 
+ 
; 
+ 
+ 
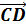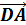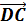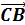
4. Дано: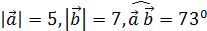 
а) Определить длины векторов: 
б) Определить скалярные произведения векторов:
а (a + b); (2 a - b)(a + 2 b); b (2 b - a);
в) Определить углы между векторами m и n, если
m = a и n = 2 a + b;
5. В правильном шестиугольнике ABCDFK задан базис AK = a; AB = b; Выразите через a и b векторы BF; CK; AD; KF; KB; CF; AF; CA; DK; BD; KD
6. Найти координаты AB, если A(-1;-2); B(4;5) и длину этого вектора.
7. Найти угол между вектором CD и осью Oy, если C(-3;4) и D(1;-2)
8. Даны точки A(-2;-3), B(2;4) и C(5;1). Разложите векторы AB; BC; CA по единичным векторам i и j.
9. Проверьте коллинеарны ли векторы AB и CD, если:
A(-3;6); B(1;2); C(4;-6); D(-2;0)
10. Дано: a = 2 i -3 j b = (-3;-4) Найти: ab; | 2 b -3 a |, угол между векторами a и b
11. Дан DABC A(4;0); B(7;4); C(-4;6) Найдите периметр DABC
12. Найти углы DABC, если A(6;2); B(-1;4); C(1;-5)
13. Найдите точку, равноудалённую от точек A(7;-1); B(-2;2); C(-1;-5)
14. Дано: a = - i - 2 j + 2 k, b = i + 2 j - 3 k. Найти: a∙b; 
; | b – a |
15. Дано: a = (-2;y;-1) и b = (3;-2;1). Найдите координату y, если известно, что a ^ b
16. Найти площадь параллелограмма, построенного на векторах:
a = 2 i + j + 2 k b = 3 i + 2 j + 2 k
17. Дано: a = (2;2;-1) и b = (-3;6;-6) Найти: (ab); [ a b ]; | 2 b – a |
Прямая линия и её уравнения
18. Проверить, принадлежат ли точки A (3;14); B(4;13) прямой 7x - 3y + 21 = 0
19. Прямая, параллельная оси Ox, проходит через точку (-2;2) Составить уравнение этой прямой.
20. Составить уравнение прямой, проходящей через точку M(3;-5) и перпендикулярной вектору n = (4;2)
21. Составить уравнение прямой, проходящей через начало координат и точку A(2;-3)
|
|
|
22. Составьте уравнение прямой, проходящей через точки A(6;7) и B(-2;3)
23. Составить уравнение прямой, проходящей через начало координат и образующей с положительным направлениям оси угол: а) 0°; б) 30°
24. Найти угол, образуемый с положительным направлением оси Ox прямой
y =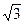 
x;
25. Преобразуйте уравнение прямой x+y-3=0 к уравнению в отрезках на осях.
26. Составьте уравнение прямой, проходящей через точку (2; 6) и образующей с осью Ox угол a = 120°;
27. Найдите угловые коэффициенты прямой 4x - 2y +9 = 0;
28. Найдите острый угол между прямыми x + 3y -2 = 0 и 2y = x +5
29. Уравнения сторон треугольника имеют вид: y = x; x + 2y + 3=0 и 
Найдите координаты вершин треугольника.
30. Докажите, что прямые 7x - 2y + 14 = 0 и 2x + 7y -20 = 0 перпендикулярны.
31. Составьте уравнение прямой, проходящей через точку Mo(-2;-3) и перпендикулярной вектору AB, если A(-5;2); B(-1;4);
32. Составьте уравнение прямой, проходящей через точку М(-3;-1) параллельно прямой АВ, если A(-2;6); B(3;-1);
33. Точки A(-6;1); B(3;6); C(6;-5) - вершины треугольника. Составьте уравнения прямых, содержащих его сторон.
34. Найдите центр и радиус сферы:
a. x2 + y2 + z2 = 16;
b. (x – 1)2 + (y + 3)2 + (z – 5)2 = 36;
35. Сфера имеет центр в точке О (2; –1; 3) и проходит через начало координат. Составьте уравнение сферы.
36. Точка А (4; – 2; 3) лежит на сфере с центром С (2; – 3; – 1). Составить уравнение сферы.
Раздел № 2 (Базовый, максимальная оценка – «отлично»)
Векторы на плоскости и в пространстве.
37. Дан тетраэдр ABCD. Докажите, что AD + BC = BD + AC
38. Дан параллелограмм ABCD и вне его произвольная точка O. Докажите, что OA + OC = OB + OD
39. Векторы a, b, c, m, модули которых | a | = 2 | b | = 3; | c | = 7; | m | = 5 образуют с осью L соответственно углы 60°; 180°; 150°; 30°. Найдите проекцию суммы этих векторов на ось L (аналитически и графически)
40. Даны векторы a = 12 i - 3 j - 4 k; b = i + 2 j + 4 k и c = i - 3 j - 2 k. Вычислите проекцию вектора b + c на вектор a
41. Докажите, что четырёхугольник с вершинами A (3;-1;2); B(1;2-1); C(-1;1-3); D(3;-5;3) - трапеция.
|
|
|
Прямая линия и её уравнения
42. Вычислить длину отрезка прямой 3x + 4y - 24 = 0, заключённого между осями координат.
43. Сторона квадрата равна 
, одна из его вершин совпадает с началом координат, а диагональ лежит на положительной полуоси Oy. Составьте уравнения сторон квадрата.
44. Составьте уравнение прямой, проходящей через точку (2; 6) и образующей с осью Ox угол α=arctg5.
45. Точки A(3;2); B(-2;1); C(1;-4) служат вершинами параллелограмма, причём A и С - противоположные вершины. Найдите четвёртую вершину D
46. Треугольник задан вершинами A(-3;4); B(-4;-3); C(8;1) Составьте уравнения: медианы AD; высоты BK
47. Треугольник задан вершинами A(2;-1); B(-7;3); C(-1;-5) Составить уравнение биссектрисы угла C
48. Дан треугольник с вершинами A(6;8); B(2;-4); C(-6;4). Найдите угол между стороной AB и медианой, проведённой из вершины A.
49. Составьте уравнение прямой, проходящей через точку пересечения прямых x + 2y + 4 = 0 и 3x - y - 9 = 0 перпендикулярно прямой x + y -7 = 0
50. Составьте уравнения высот треугольника, вершинами которого служат точки (-4;2); (6;5); (1;-4)
51. Найдите центр и радиус сферы:
x2– 6x + y2 + 8y + z2 – 4z + 4 = 0;
|
|
|
