 |
высшей квалификационной категории ГБПОУ «ЮУМК»
|
|
|
|
Министерство образования и науки Челябинской области
Государственное бюджетное профессиональное
Образовательное учреждение
«Южно-Уральский многопрофильный колледж»
Олимпиадные задания с решением по УД «Математика»
Для студентов 1 курса ГБПОУ «ЮУМК»
1. Вычислить: 
(2 балла)
2. Дано: 
Найдите: 
(2 балла)
3. Решить уравнение: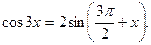 
(3 балла)
4. Решить неравенство: 
(3 балла)
5. Найдите производную функции: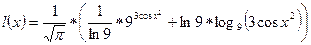 
и вычислить в точке 
. (4балла)
6. При каких a уравнение 
имеет решение и решить данное уравнение. (6 баллов)
7. Сравнить выражения: 16 log4 
и arccos (- 
). (3 балла)
8. Проверить на равносильность уравнения:
и 
(3 балла)
9. Упростить выражение:
+ 
- 
. (5 баллов)
10. Задача. В одном саду росли четыре цветка: Роза, Тюльпан, Ирис и Гладиолус.
Но это были не простые цветы. Каждый зацветал в определенное время суток: утром, днем, вечером или ночью. Хозяйка сада, всегда поливая розы, поливает и вечерние цветы сразу. Она точно знает, что утренние цветы нельзя подкармливать теми же удобрениями, что и ирис, а тюльпаны требуют того же ухода, что и цветы, расцветающие ночью. Однажды в журнале хозяйка вычитала, что розы, ирисы и гладиолусы, ни в коем случае нельзя сажать рядом с дневными цветами. Она очень удивилась, потому что розы у нее всегда росли рядом с тюльпанами, а ирисы – рядом с вечерними цветами. Какие цветы расцветают, в какое время суток? (9 баллов)
Итого: 40 баллов
Подготовила: Кондратьева Евдокия Андреевна, преподаватель ГБПОУ «ЮУМК» высшей квалификационной категории УД «Математика»
Задания с решением для олимпиады рассмотрены, обсуждены и утверждены цикловой методической комиссией блока математических и ЕН дисциплин
|
|
|
«29» марта2017 г. Протокол №7
Председатель цикловой методической комиссии ______________/О.Н.Суханова
Приложение:
Задания с решением
(на 4 страницах)
Задание 1 (2 балла).
Вычислить:
Решение:
Перейдём к основанию 3. Имеем: 
= 
Ответ: 
Задание 2 (2 балла).
Дано: Найдите:
Решение:
Использовав формулы сокращённого умножения и 
, с учётом условия задания имеем: 
= 
Ответ: 18.
Задание 3 (3 балла).
Решить уравнение: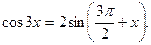
Решение:
Применив формулу тройного аргумента: 
и формулу приведения: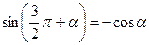 
, представим заданное уравнение в виде:
Ответ: 
; 
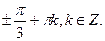
Задание 4 (3 балла).
Решить неравенство:
Решение:
Используем свойства степеней, получим:
Замена: 
Переходим к квадратному неравенству:
значит 
Подставляя 
вместо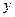 
, получим
но 
- всегда, значит 
не имеет решение.
Ответ: 
Задание 5 (4 балла).
Найдите производную функции: .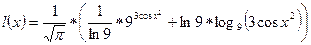
Решение:
Производная данной функции находится как производная суммы сложных функций:
в точке 
получим:
Ответ: -83.
Задание 6 (6 баллов).
При каких a уравнение имеет решение, и решить данное уравнение.
Решение:
ОДЗ. 
Логарифмируем обе части уравнения по основанию 10, получим:
Используем свойства логарифмов:
по формуле перехода логарифма от основания а к основанию 10 имеем:
Замена: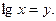 
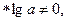
Если 
(из ОДЗ), то уравнение имеет решение:
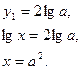
Ответ: при и 
уравнение имеет 2 решения: 
и 
.
Задание 7 (3 балла).
Сравнить выражения: 16 log4 и arccos (- ).
Ответ: 16 log4 < arccos (- ).
Задание 8 (3 балла).
Проверить на равносильность уравнения:
и .
Ответ: Уравнения не являются равносильными, т. к. их решения не совпадают.
Задание 9 (5 баллов).
Упростить выражение:
+ - .
Ответ: 0.
Задание 10 (9 баллов).
Задача. В одном саду росли четыре цветка: Роза, Тюльпан, Ирис и Гладиолус.
Но это были не простые цветы. Каждый зацветал в определенное время суток: утром, днем, вечером или ночью. Хозяйка сада, всегда поливая розы, поливает и вечерние цветы сразу. Она точно знает, что утренние цветы нельзя подкармливать теми же удобрениями, что и ирис, а тюльпаны требуют того же ухода, что и цветы, расцветающие ночью. Однажды в журнале хозяйка вычитала, что розы, ирисы и гладиолусы, ни в коем случае нельзя сажать рядом с дневными цветами. Она очень удивилась, потому что розы у нее всегда росли рядом с тюльпанами, а ирисы – рядом с вечерними цветами. Какие цветы расцветают, в какое время суток?
|
|
|
Решение:
| утро | день | вечер | ночь | |
| Розы | + | – | – | – |
| Тюльпан | – | + | – | – |
| Ирис | – | – | – | + |
| Гладиолус | – | – | + | – |
Итого: 40 баллов
Подготовила: Кондратьева Евдокия Андреевна, преподаватель математики
высшей квалификационной категории ГБПОУ «ЮУМК»
|
|
|
