 |
Компандирование по закону А (13-сегментное кодирование)
|
|
|
|
При этом законе весь дипазон амплитуд измеряется с помощью 4096 квантов (в данном случае они выполняют функции единиц измерения амплитуды). Весь диапазон амплитуд разбивается на 8 сегментов, включая нулевой (0,..., 7 или в двоичной системе 000,..., 111). В каждом сегменте для измерения применяются 16 шагов квантования различной величины (в двоичной системе они нумеруются от 0000 до 1111). При переходе от сегмента к сегменту величина шага квантования внутри сегмента увеличивается в 2 раза. Исключение составляют первые два сегмента, в которых шаги квантования равны 2. Если шаг квантования в нулевом и первом сегменте принять за 2 кванта, то во втором сегменте этот шаг составляет 4 кванта, в третьем 8 и последнем, восьмом 27 = 128 квантов. С уменьшением шага точность квантования возрастает в два раза. Соответственно, уменьшается абсолютное значение ошибки квантования (напомним, что она равна половине шага квантования). Относительная ошибка на всех шагах приблизительно одинакова и определяется разбросом амплитуд конкретного сигнала в данном сегменте.
Число шагов квантования в каждом сегменте составляет 16. Величина шагов, как указывалось, разная. Код, передаваемый в линию, содержит в 1-м разряде знак значения сигнала (положительное — отрицательное), следующие 3 разряда — номер одного из восьми сегментов, и 4 разряда — номер шага внутри сегмента. Таким образом, вместо передачи 13-разрядных комбинаций, образуемых на входе при 8192 квантах, в линию передаются 8 разрядов. Исходя из сказанного выше, структура байта, передаваемого на линию, имеет вид, представленный
| Рис. 1.28.Структура байта, передаваемого в линию при компандировании по закону А |
 |
|
|
|
Описанную процедуру называют сжатием диапазона передаваемой мощности (компрессия). На приемном конце информация приблизительно восстанавливается (расширяется — экс-пандируется). Поэтому эту операцию (обычно выполняемую специальным диодом с нелинейной характеристикой), называют компандированием (компрессия — экспандирование).
В настоящее время компрессия выполняется внутри аналого-цифрового преобразователя (кодера), а экспандирование — декодера. Оба прибора объединяются в один элемент, называемый кодеком.
Согласно принятому правилу компрессии, каждый сегмент содержит 16 шагов кванто
вания, которые вместе с номером сегмента позволяют установить значения дискреты с точ
ностью, определяемой номером сегмента.
Первый сегмент состоит как бы из двух частей: нулевой подсегмент с номером 000 кодирует отрицательную часть первого сегмента, а 001 — положительную. Остальные 6 сегментов будут сопровождаться знаком в первом разряде, поэтому их нумерация будет зависеть только от величины дискрет. Таким образом, для нумерации сегментов требуется три бита (значения номеров от 000 до 111).
При 13-сегментном кодировании кодек передает 12-разрядную комбинцию. Этого числа разрядов вполне хватает, чтобы закодировать сигнал с максимальным значением 4096 дискрет. При этом номер сегмента можно определить по положению первой единицы в этой двоичной комбинации.
Как известно, двоичный весовой код переводится в десятичный с помощью весов, присваиваемых разрядам.
N = а1211+a2210+... + а1121+а1220 = a12048 + a21024 +... + a112 + al2.
Начальные точки сегментов равны 0, 32, 64, 128, 256, 512, 1024, 2048.
Поэтому, согласно весовому уравнению, все коды последнего сегмента (7-го, с учетом отсчета от нуля) будут начинаться с 1 (единицы в старшем 12-м разряде с учетом отсчета от нуля), т.е. в общем виде 1 ххх хххх хххх. Все коды 6-го сегмента будут иметь старший нулевой разряд и значение 1 в одиннадцатом разряде и т.д., т.е. 01хх хххх хххх. Первый сегмент будет иметь все нули в старших разрядах и единицу в шестом. Наконец, нулевой сегмент будет иметь не менее семи нулей до первого разряда, обозначающего значения кванта. Поэтому правило определения номера сегмента следующее: его номер N определяется как
|
|
|
N = 7 - п, где п — номер первого единичного разряда справа в 12-разрядной двоичной комбинации.
В табл. 1.2 приводятся линейные коды и соответствующие им коды сегментов.
Таблица 1.2. Линейные коды и соответствующие им коды сегментов
| Кодовая линейная комбинация | Десятичный номер сегмента | Двоичный номер сегмента |
| 0000000xxxxx | ||
| 0000001xxxxx | ||
| 000001xxxxxx | ||
| 00001xxxxxxx | ||
| 0001xxxxxxxx | ||
| 001xxxxxxxxx | ||
| 01xxxxxxxxxx | ||
| 1xxxxxxxxxxx |
Рассмотрим значение последних разрядов 12-разрядной комбинации. Они определяют шаг квантования к, который может быть равен 2, 4, 8, 16, 32, 64, 128. Он связан с номером сегмента:
к = 2С,
где С — номер сегмента (1, 2, 3,..., 7).
Напомним, что у двух первых сегментов одинаковый шаг — 2.
Точность шага квантования позволяет определить число последних разрядов, которые можно не передавать в линию, поскольку в данном диапазоне они не влияют на величину дискреты. Например, при шаге квантования к = 4 сигналы величиной от 64 до 68 дискрет имеют одно и то же значение, т.е. последние два разряда могут игнорироваться. Учитывая это, с увеличением номера сегмента уменьшается число передаваемых последних бит, как это показано в табл. 1.3. На приемном конце принятая комбинация округляется до половины шага. В таблице латинские буквы w, х, у, z обозначают номер одного из 16-ти шагов квантования в данном сегменте. Прочерки в конце указывают на то, что выбранный шаг квантования не учитывает эти разряды и они игнорируется. В правой части таблицы приводятся 7-разрядные комбинации, передаваемые в канал.
Таблица 1.3. Линейные комбинации, передаваемые в канал согласно закону А
| Кодовая линейная комбинация | Комбинация, передаваемая в канал |
| 0000000wxyz- | 000 wxyz |
| 0000001 wxyz- | 001wxyz |
| 000001 wxyz-- | 010wxyz |
| 00001 wxyz--- | 011wxyz |
| 000lwxyz--------------------- | 100wxyz |
| 00lwxyz---------------------- | 101 wxyz |
| 0lwxyz.............................. | 110 wxyz |
| lwxyz................................ | 111 wxyz |
На приемном конце принятая комбинация округляется до половины шага квантования, что равно добавлению единичного значения предыдущего сегмента вместо непереданного разряда. Непереданные разряды дополняются нулями, число которых определяется в соответствии с номером сегмента. Нули в сегментах добавляются следующим образом:
|
|
|
- в нулевом сегменте — ни одного нуля;
- в первом — ни одного нуля (одинаковая точность);
- во втором — один;
- в третьем — два и т.д.
Восстановление последовательностей на приемном конце (экспандирование) показано в табл. 1.4.
В табл. 1.5 приводятся конкретные значения кодирования для сегментной характеристики с законом А [8]. Надо отметить, что указанный диапазон входных амплитуд дублируется в конечных точках. Поэтому обычно шаг квантования выбирается так, чтобы невозможно было получить значение отсчета, точно равное граничному значению.
Таблица 1.4. Восстановление компенсированных комбинаций на приемном конце согласно закону А
| Кодовые комбинации, полученные при компрессировании | Кодовые комбинации линейного выхода |
| 000 wxyz | 0000000 wxyzl |
| 001wxyz | 0000001 wxyz 1 |
| 010 wxyz | 00000lwxyzl0 |
| 011 wxyz | 00001 wxyz 100 |
| 100 wxyz | 0001 wxyz 1000 |
| 101wxyz | 001 wxyz 10000 |
| 110 wxyz | 01 wxyzl00000 |
| 111 wxyz | 1 wxyz1000000 |
Таблица 1.5. Кодирование сегментов согласно закону А
| Диапазон входных амплитуд | Размер шага | Код сегмента | Код шага* квантования | Амплитуда на выходе декодера |
| 0-2 | ||||
| 2-4 | ||||
| 30-32 | ||||
| 32-34 | ||||
| 62-64 | ||||
| 64-68 | ||||
| 124-128 | ||||
| 128-136 | ||||
| 248-256 | ||||
| 256-272 | ||||
| 496-512 | ||||
| 512-544 | ||||
| 992-1024 | ||||
| 1024-1088 | ||||
| 1984-2048 | ||||
| 2048-2176 | ||||
| 3968-4096 | ||||
| Все биты инвертируются через один разряд. |
Закон компандирования µ
Этот закон отличается большим числом дискрет для кодирования сигнала. Их — 8159, что позволяет более точно кодировать слабые сигналы. По статистике их больше, чем сигналов с большой амплитудой. Это обстоятельство повышает качество речи (но, как показала практика, незначительно). При этом шаги квантования меняются в каждом сегменте и равны 1, 2, 4, 8, 16, 32, 64, 128, 256. Ниже приводится таблица кодирования (табл. 1.6).
|
|
|
Таблица 1.6. Кодирование сегментов согласно закону µ
| Диапазон входных амплитуд | Размер шага | Код сегмента* | Код шага квантования | Амплитуда на выходе декодера |
| 0-1 | ||||
| 1-3 | ||||
| 3-5 | ||||
| 29-31 | ||||
| 31-35 | ||||
| 91-95 | ||||
| 95-103 | ||||
| 215-223 | ||||
| 223-239 | ||||
| 463-479 | ||||
| 479-511 | ||||
| 959-991 | ||||
| 991-1055 | ||||
| 1951-2015 | ||||
| 2015-2143 | ||||
| 3935-4063 | ||||
| 4063-4319 | ||||
| 7903-8159 | ||||
| * Все значения кодов | ыx комбинаций и | нвертируются. |
Получение кода для передачи в линию в данном случае немного сложнее, чем при использовании А-закона. Кодированию подлежат значения отсчетов, увеличенные на 33. На приемном конце после декодирования полученное значение надо уменьшить на эту величину.
Номер сегмента здесь определяется по положению «ведущей» единицы (при законе А этой единицы в первом сегменте нет) и так же, как в предыдущем случае, равно разности между числом нулей до первой единицы слева и цифрой 7 (объяснение этого факта аналогично объяснению для А-закона и следует из принципов двоичной нумерации).
Значение кода шага квантования определяется, как и в предыдущем случае, отбрасыванием младших разрядов в соответствии с точностью квантования, принятой на данном шаге.
Декодирование производится путем подстановки на место отброшенных разрядов комбинации из единицы в старшем разряде и остальных нулей. Процессы кодирования и декодирования показаны в табл. 1.7 и 1.8. Число разрядов в получаемой линейной комбинации равно 13 (для отображения максимального значения, равного 8159).
Таблица 1.7. Линейные комбинации, передаваемые в канал согласно закону µ
| Кодовая линейная комбинация | Комбинация, передаваемая в канал |
| 0000001 wxyz- | 000 wxyz |
| 00000 lwxyz-- | 001wxyz |
| 0000 lwxyz-- | 010wxyz |
| 0000 lwxyz----------------- | 011 wxyz |
| OOOlwxyz.......................... | 100wxyz |
| OOlwxyz............................. | 101 wxyz |
| Olwxyz................................ | 110wxyz |
| lwxyz.................................. | 111 wxyz |
Таблица 1.8. Восстановление компрессированных комбинаций на приемном конце согласно закону µ
| Кодовые комбинации, полученные при компрессировании | Кодовые комбинации линейного выхода |
| 000 wxyz | 00000001 wxyzl |
| 001 wxyz | 000000 lwxyz 10 |
| 010wxyz | 00000 lwxyz 100 |
| 011 wxyz | 0000 lwxyz 1000 |
| 100 wxyz | 000 lwxyz 10000 |
| 101 wxyz | 001 wxyzl 00000 |
| 110 wxyz | 01 wxyzl 000000 |
| 111 wxyz | lwxyz10000000 |
|
|
|
Мультиплексирование
Сигналы, полученные методом ИКМ, позволяют мультиплексировать информацию по времени. Для этого периодически подаваемые сигналы одного канала надо сдвинуть по времени относительно сигналов другого канала так, чтобы они поступали во время паузы в первом, как это показано на рис. 1.29. На нем показаны четыре канала, по каждому из которых периодически поступает информация. При объединении в один тракт эти сигналы поступают в определенные промежутки времени.
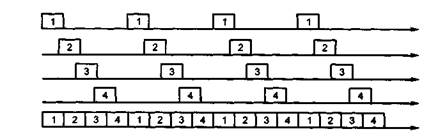
Рис. 1.29. Принцип мультиплексирования
В наиболее распространенной для Европы системе ИКМ, которая легла в основу всех цифровых систем коммутации, количество каналов в одном цифровом тракте равно 32.
Если вспомнить, что для каждого цифрового канала надо передавать 64 килобита в одну секунду, то для передачи 32 каналов требуется передавать 2048 килобит в секунду.
|
|
|


