Решение истинностных задач

Логические операции

(логическое умножение) F = А Λ B	Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны входящие в него простые высказывания. Например, рассмотрим составное высказывание "2*2=4 и 3*3=10". Первое простое высказывание (2*2=4) истинно (А=1), а второе высказывание (3*3=10) ложно (В=0), по таблице определяем, что логическая функция принимает значение ложь (F=0), т.е. данное составное высказывание ложно.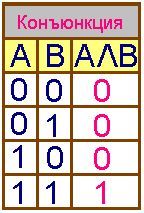
(логическое сложение) F = А V B	Составное высказывание, образованное в результате операции логического сложения (дизъюнкции), истинно тогда, когда истинны хотя бы одно из входящих в него простых высказываний. Например, рассмотрим составное высказывание "2*2=4 или 3*3=10". Первое простое высказывание (2*2=4) истинно (А=1), а второе высказывание (3*3=10) ложно (В=0), по таблице определяем, что логическая функция принимает значение истина (F=1), т.е. данное составное высказывание истинно.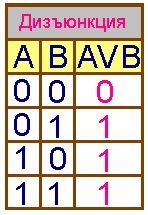
(логическое отрицание) F = А	Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное - истинным. Например, А=(2*2=4)=1(ИСТИНА) А = 0 В=(3*3=10)=0(ЛОЖЬ) В = 1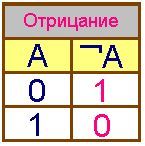
(логическое следование) F = А => B	Составное высказывание, образованное в результате операции логического следование (импликации), ложна тогда и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание). Логическое следование(импликация) образуется соединением двух высказываний в одно с помощью оборота речи "если..., то..."
(логическое равенство) F = А <=> B	Составное высказывание, образованное с помощью логической операции эквивалентности, истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны. Логическое равенство(эквивалентность) образуется соединением двух высказываний в одно с помощью оборота речи "...тогда и только тогда, когда..."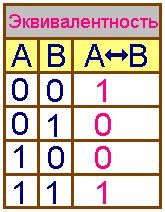
преобразования логических выражений	А = А (закон двойного отрицание) (А Λ В) = А V B (законы (А V В) = А Λ B Моргана) А => В = А V B (А => В) = А Λ B А <=> В =(А Λ B) V (А Λ B) А Λ А = 0 (закон непротиворечия) А V А = 1 (закон исключенного третьего)
	Законы коммутативности: (А Λ В) ≡ (В Λ А); (А V В) ≡ (В V А); Законы ассоциативности: (А V В) V С ≡ А V (В V С); (А Λ В) Λ С ≡ А Λ (В Λ С); Законы дистрибутивности: А Λ (В V С) ≡ (А Λ В) V (А Λ С) А V (В Λ С) ≡ (А V В) Λ (А V С)
	Значение логической функции можно определить с помощью таблицы истинности данной функции, которая показывает какие значения принимает логическая функция при всех возможных наборах её аргументов.
Задача №43 стр. 59: Алеша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предложения: Алеша: "Это сосуд греческий и изготовлен в V веке". Боря: "Это сосуд финикийский и изготовлен в III веке". Гриша: "Это сосуд не греческий и изготовлен в IV веке". Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предложений. Где и в каком веке изготовлен сосуд?	Решение: А = "Это сосуд греческий"; B = " Изготовлен в V веке"; C = " Изготовлен в IV веке "; D = "Изготовлен в III веке"; E = "Это сосуд финикийский ".   А В С D E Алеша + +       Боря       + + Гриша -   +     1. Если А =1(истина), то В=0; А=1,то Е=0, тогда D=1; А=0, С=0, а это не может быть, по условию А или С истина. 2. Пусть А=0 и В=1; Тогда Е=1 а D=0; и А=1, то С=0; в итоге получим В=1 и Е=1, т. е. сосуд финикийский и изготовлен в V веке.
Задача №44 стр. 59: В нарушении правил обмена валюты подозреваются четыре работника банка - А, В, С и D. Известно, что: Если А нарушил, то и В нарушил правила обмена валюты. Если В нарушил, то и С нарушил или А не нарушил. Если D не нарушил, то А нарушил, а С не нарушил. Если D нарушил, то и А нарушил. Кто из подозреваемых нарушил правила обмена валюты? Решите задачу с помощью логических операций.	Решение: А => B; B => C V А; D => A Λ C; D => A Произведение всех высказываний =1. (А => B)Λ(B => C V А)Λ(D => A Λ C)Λ (D => A) = 1 а выражение справедлива тогда и только тогда, когда А => B = 1; B => C V А) = 1; D => A Λ C = 1; D => A = 1; Составим таблицу истинности для этого выражения: A B C D А => B D => A C V А) B => C V А) A Λ C D => A Λ C F                                                                                                                                                                                                                                                                                                                                                                 Ответ: А=1,B=1,C=1,D=1, т.е. все подозреваемые нарушили правила обмена валюты.

1 Алгоритм построения таблицы истинности:

1. подсчитать количество переменных в формуле;
2. определить число строк в таблице m = 2 ⁿ, где n – количество переменных;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов в таблице: число переменных + число операций;
6. выписать наборы значений переменных, входящих в формулу;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в п. 4, очередностью выполнения.

2 Для решения логических задач необходимо:

1. выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами;
2. записать условие задачи на языке алгебры логики, соединив простые высказывания в сложные с помощью логических операций;
3. составить единое логическое выражение для всех требований задачи;
4. используя законы алгебры логики, попытаться упростить полученное выражение и вычислить все его значения либо построить таблицу истинности для рассматриваемого выражения;
5. Выбрать решение – набор значений простых высказываний, при котором построенное логическое выражение является истинным;
6. проверить, удовлетворяет ли полученное решение условию задачи.

Решение истинностных задач

Данный тип задач можно решать тремя методами: методом рассуждений, табличным методом и с помощью логических выражений, с помощью построения таблиц истинности и приведения задачи к системе логических уравнений.

Пример:

Перед началом Турнира «Четырех» болельщики высказали следующие предположения по поводу своих кумиров:

А) Макс победит, Билл – второй;

В) Билл – третий, Ник – первый;

С) Макс – последний, а первый – Джон.

Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов. Какое место на турнире заняли Джон, Ник, Билл, Макс?

Решение (способ 1, метод рассуждений):

1) Есть «точная» информация, которая не подвергается сомнению: каждый из болельщиков оказался прав в одном прогнозе.

2) Запишем высказывания болельщиков:

1. Макс победит, Билл – второй;
2. Билл – третий, Ник – первый;
3. Макс – последний, а первый – Джон.

3) Известно, что каждый из болельщиков только в одном из прогнозов был прав (то есть, из двух высказываний одно истинно, а другое – ложно).

4) Пусть первый болельщик угадал, что Макс победит, тогда третий болельщик ошибся в двух предположениях, а это не соответствует «точной» информации.

5) Пусть первый болельщик угадал, что Билл занял второе место, тогда второй болельщик предсказал первое место Нику, следовательно, по предположению третьего, Макс занял последнее место, а Джон – оставшееся третье место.

Отсюда имеем: Ник – первое, Билл – второе, Джон – третье и Макс – четвертое место.

Решение (способ 2, табличный метод):

Основной прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи.

1) Запишем высказывания трех болельщиков в форме таблицы (заголовок строки обозначает место в турнирной таблице):

 

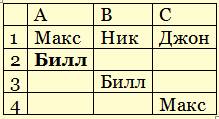
2) Считая, что два человека не могут оказаться на одном месте, начнем «раскручивать» эту таблицу с той строчки, где больше всего информации (в данном случае – с первой).

3) Предположим, что Макс действительно занял первое место, как и сказал «A»; в этом случае:

 

• «C» ошибся, поставив на первое место Джона;
• учитывая, что каждый один раз угадал, а второй ошибся, получается, что «C» угадал, что Макс будет на четвертом месте;
• но мы предположили, что Макс – на первом месте (а не на четвертом), следовательно, получили противоречие; это значит, что Макс все-таки не на первом месте
• таким образом, в первом прогнозе «А» ошибся, это значит, что во втором он угадал, и Билл действительно занял второе место:

 

• так как Билл – второй, он не может быть на третьем месте, поэтому из прогноза «Б» следует, что Ник – первый:

 

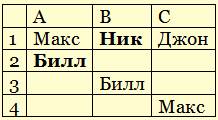
• если Ник на первом месте, там не может быть Джон, поэтому из ответов «С» (среди которых должен быть один верный, и один неверный), сразу находим, что Макс занял четвертое место:

 

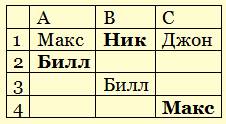
4) осталось только определиться с Джоном – ему досталось единственное «свободное» третье место; окончательный список победителей:

Ник

Билл

Джон

Макс.

 

Пример:

В школе-новостройке в каждой из двух аудиторий может находится либо кабинет информатики, либо кабинет физики. На дверях аудиторий повесили шутливые таблички. На первой повесили табличку «По крайней мере, в одном из этих аудиторий размещается кабинет информатики», а на второй аудитории – табличку с надписью «Кабинет физики находится в другой аудитории». Проверяющему, который пришел в школу, известно только, что надписи на табличках либо обе истины, либо обе ложны. Помогите проверяющему найти кабинет информатики.

Решение (способ 3, логические выражения):

Переведем условие задачи на язык логики высказываний. Так как в каждой из аудиторий может находиться кабинет информатики, то пусть:

А = «В первой аудитории находится кабинет информатики»;

В = «Во второй аудитории находится кабинет информатики».

Отрицания этих высказываний:

А =«В первой аудитории находится кабинет физики»;

В = «Во второй аудитории находится кабинет физики».

Х = А ˅ В.

Высказывание на второй двери:

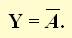
Утверждение о том, что надписи на табличках либо одновременно истинные, либо одновременно ложные в соответствии с законом исключенного третьего запишется следующим образом:

Подставим вместо X и Y соответствующие формулы:

Упростим сначала первое слагаемое. В соответствии с законом дистрибутивности умножения относительно сложения:

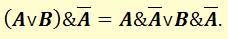
В соответствии закона непротиворечия:

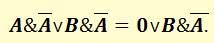
Далее упростим второе слагаемое. В соответствии с первым законом де Моргана и законом двойного отрицания:

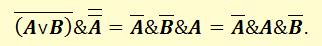
В соответствии с законом непротиворечия:

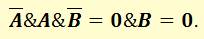
В результате получаем:

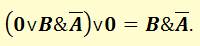
Построим таблицу истинности для полученного выражения:

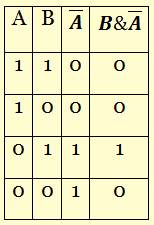
Проанализировав данные таблицы истинности имеем, что в первой аудитории находится кабинет физики, а во второй – кабинет информатики.

 

Пример:

Следующие два высказывания истинны:

(1). Неверно, что если корабль A вышел в море, то корабль C — нет.

(2). В море вышел корабль B или корабль C, но не оба вместе.

Определить, какие корабли вышли в море.

Решение (способ 4, система логических уравнений):

Обозначим буквами высказывания:

A — «корабль A вышел в море»,

B — «корабль B вышел в море»,

C — «корабль C вышел в море».

Высказывание «если корабль A вышел в море, то корабль C — нет» можно записать в виде:

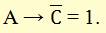
По условию (1), это высказывание неверно, таким образом, имеем:

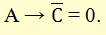
Кроме того, из (2) получаем:

Таким образом, решение задачи сводится к решению системы логических уравнений:

Нужно найти тройку логических значений A, B и C, при которых оба уравнения превращаются в истинные равенства. Рассмотрим несколько способов решения этой системы.

Поделиться:

Воспользуйтесь поиском по сайту: