 |
Пример выполнения контрольной работы № 2
|
|
|
|
КОНТРОЛЬНАЯ РАБОТА № 2. ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ
В ЛОГИКЕ ВЫСКАЗЫВАНИЙ
Теоретические сведения
Определение. Формула 
называется логическим следствием формул 
, если она обращается в истинное высказывание на всяком наборе значений переменных, для которого в истинные высказывания обращаются все формулы 
. Для обозначения логического следования используется знак 
; таким образом, 
.
Нахождение следствий из посылок (алгоритм 1): если имеется конечное число формул (посылок) 
и требуется найти все формулы, являющиеся логическими следствиями данных посылок, то следует:
1) привести конъюнкцию 
посылок к СКН-форме;
2) перечислить все совершенные дизъюнктивные одночлены, входящие в СКНФ, а также всевозможные конъюнкции этих одночленов по два, по три и т.д.;
3) придать формулам, полученным на предыдущем шаге, более удобную равносильную форму и записать их в ответ: именно этот набор формул и будет исчерпывать совокупность всех логических следствий из данных посылок.
Нахождение посылок для данных следствий (алгоритм 2): если имеется формула и требуется найти все формулы, логическим следствием каждой из которых будет формула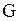 
, то следует:
1) найти СКН-форму для заданной формулы-следствия 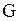и выявить совершенные дизъюнктивные одночлены от переменных 
, которые в ней отсутствуют;
2) затем составить конъюнкции формулы 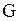с этими недостающими одночленами, взятыми по одному, по два, по три и т.д.;
3) полученная совокупность формул будет искомой (с точностью до равносильности формул).
Задание к контрольной работе № 2
1) Методом от противного выяснить, верно ли предложенное логическое следование. Справедливость полученного вывода подтвердить решением этой же задачи на основе определения понятия логического следования.
|
|
|
2) Найти все не равносильные между собой и не тождественно истинные формулы алгебры высказываний, являющиеся логическими следствиями заданных формул-посылок 
.
3) Найти все не равносильные между собой и не тождественно ложные формулы алгебры высказываний, для которых заданная формула 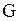является логическим следствием.
Таблица − Варианты заданий к контрольной работе № 2
| № вар. | Установить, верно ли логическое следование | Найти все следствия из ука- занных посылок | Найти все посылки, приводя-щие к указан- ному следствию |
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
|
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
|
| ||
|
|
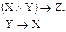
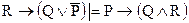
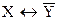
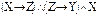
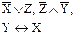
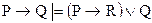
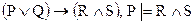
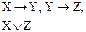
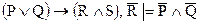
Пример выполнения контрольной работы № 2
I. Выяснить, выполняется ли следующее логическое следование:
.
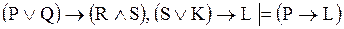Решение. Предположим, что данное следование не выполняется, то есть
.
На основании определения операции импликации отсюда следует система двух логических равенств, которая при их совместности будет указывать на правомерность предположения о невыполнимости исследуемого логического следования, тогда как их несовместность будет влечь за собой положительный ответ на вопрос задачи.
Итак, имеем
Из второго уравнения системы находим: 
. При этих значениях пропозициональных переменных 
и 
первое уравнение системы принимает вид
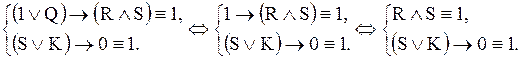
Продолжая цепочку равносильных систем, находим
|
|
|
с определением импликации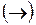 
!
Таким образом, предположение о невыполнимости заданного логического следования оказалось ложным и, следовательно, оно выполнимо.
Ответ: логическое следование 
истинно.
Для подтверждения правильности полученного вывода о том, что имеет место логическое следование , ввиду объемности соответствующей таблицы истинности − она должна содержать 
строки − воспользуемся алгебраическим подходом и покажем, что формула
является тавтологией, то есть тождественно истинна.
то есть формула 
является тавтологией, что доказывает факт логического следования
.
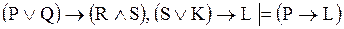II. Найти все не равносильные между собой и не тождественно ложные формулы алгебры высказываний (посылки), из которых логически следует формула 
.
Решение. Следуя алгоритму нахождения посылок для данных следствий (алгоритм 2) и полагая, что заданная формула-следствие зависит от трех аргументов 
, 
и 
, найдём её совершенную конъюнктивную нормальную форму:
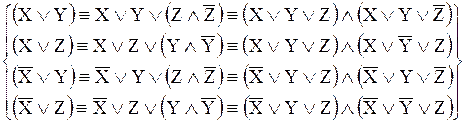
Далее, чтобы наглядно увидеть, каких совершенных дизъюнктивных одночленов от переменных , , недостаёт в полученной СКНФ для заданной формулы-следствия , целесообразно обратиться к таблице истинности этой формулы:
|
|
|
| Совершенные дизъюнкты,
входящие в
СКНФ 
|
| + | |||
| + | |||
| + | |||
| − | |||
| + | |||
| + | |||
| + | |||
| − |
Из таблицы истинности следует, что в СКНФ отсутствуют два совершенных дизъюнктивных одночлена:
− четвертая строка таблицы истинности;
− восьмая строка таблицы истинности.
Таким образом, согласно алгоритму 2, всё множество формул-посылок, зависящих от трех пропозициональных переменных , и , следствием каждой из которых будет заданная формула-следствие , будет представлено следующими формулами:
1) 
;
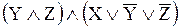2) 
;
3) 
.
Упростим полученные формулы:
1) 
2) 
3) 
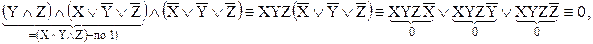
то есть тождественно ложная формула.
Требованиям задачи отвечают две формулы: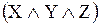 
и 
, то есть логическим следствием каждой из них является заданная в условии задачи формула-следствие .
|
|
|
| 
|
|
|
|
|
|
|
|
| 
| 
|
|
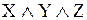
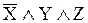
Очевидно, что из множества формул-посылок 
также следует заданная в условии задачи формула-заключение :
|
|
|
|
|
|
| 
|
|
|
|
|
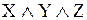
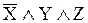
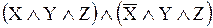
