 |
Вводится допущение: предел дельта f при дельта х стремящемся к нулю равно нулю (посмотреть, как это обосновывается, обосновывается ли).
|
|
|
|
Лекция 05.02.2019
Тема: Уравнения.
Способ решения:
1. Использование следственных переходов
 |
х2 – 5х + 6 = 0
х = 2 или х = 3
Проверка по исходному уравнению …
Ответ: 3
(или можно Ответ: х=3, но это худший вариант).
2. Равносильные переходы
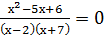
Ответ: 3.
3. Использование области определения уравнения.
Найти область определения выражений, стоящих в уравнении, избавиться от знаменателя, проверить по ОДЗ, все, что входит в ОДЗ, проверить по исходному условию.
Неравенства, решения: использование равносильности (это сложно) или творческие пути (использование свойств функции, обобщенный метод интервалов и др.
Тема: Методика введения основных тригонометрических понятий (синус, косинус, тангенс и котангенс).
К неосновным относятся арксинус и арккосинус.
Можно выделить три этапа введения тригонометрических понятий:
1) (геометрия) для острого угла через элементы прямоугольного треугольника.
(sec α = 1\cos α
2) (геометрия) для α є[0º, 180º] через элементы окружности с центром в начале координат
3) (в 10-м классе, алгебра) α - любой
Опр. Синус угла α – ордината точки Аα единичной окружности, полученной поворотом на угол α относительно начала координат точки А0 с координатами (1;0).
sin α = уАα, где Аα = Rα0(A0), А0 (1;0)
|
По уравнению окружности с центром в О (0;0) получаем основное тригонометрическое тождество.
Работая только с определением, ученики должны уметь найти и показать синус и косинус любого угла.
Методическая проблема:
1) как ввести понятие синуса, косинуса, тангенса, котангенса числа (числового аргумента).
sin 7 – это синус угла, равного 7 радиан.
|
|
|
Вводится понятие радиана. 1 радиан – мера центрального угла окружности, опирающегося на дугу, равную радиусу.
Синусом числа а называется синус угла а радиан.
2) почему для определения синуса числа выбрана именно радианная единица измерения углов.
Учащиеся на тригонометрической окружности должны различать 5 осей:
1) круговая ось для откладывания аргументов;
2) ось синусов – отрезок на Оу;
3) ось косинусов – отрезок на Ох;
4) ось тангенсов – прямая х = 1, т.к. все точки этой прямой имеют координаты (1; tg α;
5) ось котангенсов – прямая у = 1, все ее точки имеют координаты вида (ctg α; 1).
На всех четырех осях единица измерения одна и та же, а на круговой оси отличается, если работать в градусах, и совпадает, если работать в радианах. А в числовых функциях все координаты должны иметь одинаковый масштаб. Для обеспечения одинакового масштаба на всех пяти осях и выбираются радианы при переходе к числовому аргументу.
В пособиях определение разбито на 2 части: сначала объяснение, что такое точка Аα (точка, соответствующая углу альфа), затем дается определение, в котором используется термин точка, соответствующая углу альфа.
При анализе пособия: вводится ли понятие «поворот», как вводится. Хорошая модель – часы с круглым циферблатом.
Лекция 07.02.2019
Тема: Подходы к введению понятий арксинус, арккосинус, арктангенс, арккотангенс.
Эти понятия вводятся только в связи с появлением необходимости решать уравнения и неравенства.
Введение этих понятий – сразу после синуса, косинуса, тангенса, котангенса.
Несколько способов введения понятия, например, арксинуса:
1) как один из корней уравнения sin x = а, на промежутке [-п\2; п\2].
Мы хотим решить уравнение, берем а от единицы до единицы, строим график и видим, что корней очень много. Видим, что на промежутке [-п\2; п\2] есть корень, ему присваиваем «звание» арксинус а.
2) через идею обратной функции. Чтобы получить обратную функцию, надо,чтоб она была обратима (не имела повторов значений), а для этого надо, чтоб она была монотонной. Таких промежутков много, по договоренности математиков берут промежуток …
|
|
|
Для получения функции этой чертят биссектрису 1-й и 3-й координатной четверти и относительно нее отображают симметрично функцию синуса (см. у Дианы).
3) Арксинус числа в, где в принадлежит промежутку [-1; 1] называется (или угол, или число, но если это очень рано, то лучше брать угол) угол альфа, принадлежащий промежутку [-п\2; п\2], синус которого равен в, т.е. sin(arcsin b) = b.
Все подходы выходят в итоге на это определение.
b є [-1; 1], arccos b є [0; п], cos(arccos b) = b.
b є R, arctg b є (-п\2; п\2), tg(arctg b) = b.
Арккотангенс.
Чему равен синус 37 градусов? (найти по модели – распечатать предварительно из учебника).
Куча всего см у Дианы.
Лекция 07.02.2019
Тема: Методика изучения тригонометрических тождеств.
Самая большая проблема в изучении тригонометрических тождеств – их количество и запоминание.
Формулы тригонометрии можно разбить на несколько групп:
1. Формулы зависимости между тригонометрическими выражениями одного и того же угла:
а) основное тригонометрическое тождество,
б) формулы тангенса и котангенса через синус и косинус;
в) следствия из основного тригонометрического тождества (про связь между тангенсом и косинусом, котангенсом и синусом);
г) произведения тангенса и котангенса.
Всего 6 формул.
Методические проблемы по формулам: обоснование, запоминание, отработка формул в двух направлениях, применение формул в разных ситуациях.
Типичное задание на применение: известен тангенс, найти все остальные тригонометрические величины.
2. Формулы приведения
Формулы привидения + периодичность позволяют свести вычисления любой тригонометрической функции от любого аргумента к выражениям от аргументов в первой четверти.
Методические проблемы:
а) Количество формул в пособии:
0 – α, п\2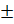 
α, 3п\2 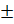α; 2п 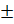α; т.е. количество формул – 28 или 32.
б) проблема обоснования:
1) с помощью определения тригонометрической функции и признаков равенства прямоугольных треугольников доказываются несколько формул (6-8) для синуса или косинуса и говорят, что можно так же доказать остальные;
|
|
|
2) с помощью определения тригонометрической функции и признаков равенства прямоугольных треугольников доказываются несколько формул (6-8) для синуса или косинуса, а все остальные формулы позже с помощью теорем сложения.
У учеников может возникнуть вопрос, почему бы все формулы приведения не обосновать с помощью теорем сложения. Но это невозможно, т.к. доказательство самих теорем сложения опирается на знание некоторых формул приведения.
Доказательство для синуса 3п\2 минус альфа и др. см. у Дианы.
В учебнике, как правило, есть доказательство для отрицательного альфа, п минус альфа, п\2 минус альфа.
в) проблема припоминания: для этого вводится мнемоническое правило.
(Мнемозина – богиня памяти).
Оно состоит из двух частей: правило названия функции, правило знака (т.е. меняется ли функция и на какую, какой знак ставить). Лучше сначала определять знак, потом название полученной функции.
3. Теоремы и формулы сложения:
а) проблемы обоснования (т.е. вывода формулы).
Существуют 3 подхода:
1) использование векторов – внепрограммный вариант;
2) использование формул площади треугольника через тригонометрию (но такое обоснование возможно только для острых и тупых углов;
3) с использованием формулы расстояния между точками координатной плоскости.
В зависимости от выбора способов обоснования в разных пособиях выбираются различные варианты формулы, которая доказывается первой.
При а) сначала доказывается косинус разности.
Доказательство у Дианы.
Скопировать доказательство через расстояния из учебника (Латотин?)
Выведение для тангенса – у Дианы.
4. Преобразования произведений синусов и косинусов в суму, разность.
5. Формулы двойного аргумента.
6. Формулы половинного аргумента (повышения и понижения степени).
Выделение и формулирование названий для разных групп формул не совпадают в разных учебниках.
Лекция 09.02.2019
ВСТ Опять об уравнениях.
f(x) + g(x) – h(x) = 0,где f(x), g(x), h(x) уравнения.
f(x) + g(x) – h(x) = 0 
- равносильность
|
|
|
f(x) + g(x) – h(x) = 0 
– следствие
f(x) + g(x) – h(x) = 0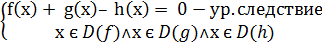 
Произведение равно нулю, если хотя бы один сомножитель равен нулю, а остальные при этом существуют.
ВСТ закончена.
7. Косинус, синус суммы и разности. Произведение синусов, косинусов.
Косинус: однородные произведения, конфронтация знаков; синус – согласование знаков, смешанные произведения.
Произведения выводятся из косинуса и синуса суммы, разности (сложить или вычесть две формулы).
Тема: Методика изучения тригонометрических уравнений.
Тригонометрическое уравнение – уравнение, в котором есть тригонометрические выражения. Строгого определения не дается.
ТУ условно разбиваются на классы:
1. Простейшие тригонометрические уравнения: sin x = a и т.д.
2. Уравнения, сводящиеся к квадратному (степенному) относительно одной из тригонометрических функций: 3sin2 x + 5sin x – 4 = 0
3. Однородные (разных степеней): 2 sin2 x + sin x cos x + 5 cos2x = 0
Признаки однородных уравнений:
- две переменных или два вида функций;
- одна и та же сумма степеней 2-х переменных (функций) в каждом слагаемом;
- отсутствие свободного члена.
Пример: 5*(3x)2 +7*2x*3x + (2x)2 = 0 – однородное уравнение второй степени относительно переменных 2x, 3х
4. Уравнение вида а sin x + b cos x = c.
Существует более 10 способов решения уравнений такого вида, на экзамене знать не менее 5, в т.ч. сведение к однородному.
И другие виды уравнений.
Насобирать коллекцию названий видов уравнений по пособиям.
Методические проблемы:
1. Классификация уравнений (мет. проблема)
1) простейшие тригонометрические уравнения.
ВСТ фомулы.
Проблема запоминания: в формулах синуса и косинуса теряют знаки, и др.
Проблема решения уравнения с параметром – рассмотреть все случаи:
Например sin x = a
1) |a|>1, тогда корней нет;
2) а є {-1; 0; 1} – частные случаи, их неприлично решать по общей формуле; расписать их по отдельности;
3) |a| < 1 х є (-1; 0) (0;1) общая формула выводится или с помощью графика функции, или с помощью тригонометрической окружности.
Этот вывод надо знать.
(К любым видам ур-ний надо уметь сказать о3-х возможных стратегиях:
1) Соблюдение равносильности
2) Следственный переход (тогда надо делать проверку)
3) Творческие подходы (св-ва функции и др).)
2. Проблема припоминания формул.
3. Проблема уровня требований (давать ли тангенс и котангенс).
4. Полнота системы упражнений.
Например, в учебнике есть частные случаи, табличные, но нет нетабличных случаев, нет случаев, когда нет решений. Или, например, разобраны все ситуации для плюса, а ситуаций для минуса только две (а ведь арккосинус с плюсами и с минусами вычисляется по-разному). Должен быть не только «голый» х (sin х = 1\2), но и (5х+8), например.
|
|
|
Правильно оформлять.
Если вводим подстановку, не писать, например, просто sin x = у. Писать словами: «Пусть sin x = у, тогда ….» (переписываем уравнение с подстановкой). Находим у1 и у2, пишем: «с учетом подстановки sin x = …» и дорешать. Кстати, ограничения на у можно не указывать (что не больше, не меньше нуля).
Решение однородных уравнений.
Делим на одну из тригонометрических функций, синус или косинус. При этом получается, мы договорились, что эта функция не принимает значение ноль. Получается, надо записать совокупность систем: косинус квадрат (например) не равен нулю и поделенное исходное уравнение в совокупности с: косинус равен нулю и уравнение с подставленным нулем вместо косинуса. Во второй системе получим пустое множество, «т.к. не выполняется основное тригонометрическое тождество». См. фото (у Дианы).
Способы решения уравнения а*sin x+ в*сos х = с
а) с помощью дополнительного угла – см. у Дианы.
Ответ – арксинус или арккосинус, арктангенс или арккотангенс – зависит от того, в какой четверти оказался угол (вспомнить, на каком промежутке рассматриваются арки).
б) сведение к однородному уравнению относительно половинного угла (синус и косинус расписываются через формулы половинного угла, с = 1*с и 1 расписывается через основное тригонометрическое тождество).
в) через сведение к системе уравнений с двумя переменными: вводятся переменные вместо синуса и косинуса, вторым в систему записываем основное тригонометрическое тождество.
г) возвести обе части в квадрат (следственный переход), получим однородное уравнение, сделать проверку корней по условию (т.к. следственный переход).
д) замена синуса на корень из 1 – cos2х; это равносильный переход, ведь синус может быть отрицательным, а корень всегда положительный.
е) универсальные подстановки (синус и косинус черезтангенс половинного угла), но при ней – запрет на х = п +2Пn, т.е. их отдельно надо проверять.
Имеет смысл выделить тригонометрические уравнения, где очень эффективны функциональные подходы (творческие пути), например, через ограничение на синус и косинус (больше -1 но меньше 1).
Лекция 28.02.19
Уравнения с обратными тригонометрическими функциями.
На зачет можно попробовать уравнение: sin(arcsin(x2)) = 4
Методика изучения тригонометрических функций.
Методические проблемы:
1. Место введения тригонометрических функций.
Подходы: а) раннее введение – сразу после введения соответствующих понятий, до формул тригонометрии (по нашей программе должно быть так); б) позднее введение – после формул: определение, тождества, только потом функции.
2. Получение графика функции: 2 подхода:
а) для синусов и косинусов соответствующее значение получают из тригонометрической окружности; как правило, все школьные учебники начинают с построения тригонометрической окружности.
Оси: …, ось аргументов – всего 5 шт.
Тригонометрический круг – совмещение единичной окружности с системой координат.
Построение графика: у нас круг, с которого мы «снимаем показания»; получаются неравномерные шаги; непривычная для учеников ситуация; появление круга как источника данных.
Т.е. первый подход: круг – график.
Второй подход (у Шнепермана): между кругом и графиком вставляется привычная для учеников табличка; и авторы стараются сделать равномерный шаг.
3. Выделение требований к линии графиков: учет асимптот и известных касательных (обычно этого в учебниках нет, только у Колмогорова, возможно, есть; обычно это функция учителя).
(Например: различие графиков тангенсоиды и кубической параболы: тангенсоида не пересекает график функции у = х!
Еще нарушение: выбор не равных единиц по осям: П должно быть примерно равно 3, а не 2, не 1.5).
4. Обучение чтению свойств функции по графику.
Соответственно, проследить, как записываются эти свойства (область определения, область значений, наименьшее значение; наибольшее и напериодичность, нули, четность, промежутки знакопостоянства, промежутки возрастания и убывания).
Чаще всего делаются ошибки при записи промежутков возрастания, знакопостоянства. Например, функция синус возрастает на каждом из промежутков [ - П/2 + 2Пn; П/2+2Пn] – т.е. точки включаются; при записи знакопостоянства точки не включаются.
5. Обоснование свойств функции.
Доказательство четности/ нечетности синуса и косинуса – в формулах приведения (через равенство треугольников).
Три проблемных вопроса: четность, периодичность, промежутки возрастания / убывания.
Пример: доказать, что функция синус на промежутке [-П/2;П/2] возрастает.
По опр.: х1, х2 принадлежат промежутку; х2>x1 (х2-х1>0)
Рассмотреть разность синусов этих аргументов, перейти от разности к произведению, оценить полученное выражение с учетом условия (см. у Дианы). Преподаватель в ярости сказала, что у каждого будет спрашивать это обоснование!!
Доказательство наименьшего положительного периода: от противного + определение.
6. Преобразование графиков тригонометрических функций.
у = а*sin(bx+c) +d
Метод рамок при построении графиков (Тригонометрия Школьный курс).
Знать, как действуют на график и уравнение функции у=f(x) следующие виды геометрических преобразований:
- осевая симетрия относительно Оу (Soy): у=f(-x);
- осевая симетрия относительно Ох (Sox): у= - f(x);
- центральная симетрия (Z0): у= - f(-x);
- действие вектором (r (a; b)): у = f(x-a)+b
- сжатие (растяжение) вдоль оси Оу (koy = k): y = kf(x)
- сжатие (растяжение) вдоль оси Ох (kox = m): y = f(x/m)
Если уравнение составлено верно, мы должны получить…?
Получить из уравнения у = sin x уравнение у = а*sin(bx+c) +d c помощью композиции преобразований: параллельный перенос, сжатие вдоль Ох, Оу.
Композиция этих преобразований не коммутативна (приложив ее в разных вариантах (возможно 6 разных порядков), мы получим разные влияния на график). Проверить это для случая: r (1;2), koy = 3, kox = 4.
Построить график… посмотреть у Дианы, это интересно!
Метод рамок: рисуют много графиков: сжатые, растянутые и др. Преобразуют не сам график, а прямоугольную рамку, в которую вписывается та или иная функция на периоде.
Плюсы: наглядность
Лекция 14.03.
Тема: Методика изучения тригонометрических неравенств (простейших).
Этот материал не входит в программу.
Но программными являются все неравенства, связанные со свойствами функции. Пример: sin >0, sin < 0, и со знаками больше\ меньше либо равно. Это неравенства, связанные с промежутками знакопостоянства. Это же для котангенса, тангенса, косинуса.
Неравенства сравнение синуса\ косинуса с единицей, с минус единицей.
(Разница между ответами: «х – любое число» и «бесконечно много решений»: может быть бесконечно много решений, но при этом х – не любое число; лучше писать не х принадлежит R, а х – любое число, т.к. х в школе всегда принадлежит R, даже если х=1).
Так что 32 тригонометрических неравенства входит в программу базовой школы).
Простейшие тригонометрические неравенства:
sin x >a (<a; 
)…
Методические проблемы:
1. Выбор способа решения: по кругу, по графику, метод интервалов.
2. Какое количество конкретных неравенств для одного вида функции дано в учебном пособии с решением.
Т.е. какое количество надо рассмотреть, чтобы было достаточно для научения.
У Шнепермана 4 для синуса.
3. Уровень сложности примера, выбранного для демонстрации (примера с решением).
4. Насколько выделен в учебном пособии алгоритм решения, можно ли его вычитать. Если он дан: насколько алгоритм работающий.
Пример: sin x < 
sin(2x – 1) 
; sin 3x 
;
разные аргументы, табличные значения, два значения положительные, два – отрацательные. На круге можно иллюстрировать только простейшие неравенства. Если оно не простейшее, надо вводить новую переменную
Алгоритм решения по кругу: свести к простейшему, определить, в какой точке (Ах1 или Ах2) можно увидеть аргфункцию. В первом неравенстве это Ах1.
Значит, х1 это арксинус 1\2 = П\6
По рисунку пройти по закрашенной дуге ко второй точке, вычислить х2, записать решение.
По графику: начертить график, закрасить ту часть графика, которая подходит; задаем вопрос: при каких аргументах появляются закрашенные части, «бросить тень» на Ох. Для записи решения давайте выберем тот интервал, который пересекается с территорией арксинусов…
Для синуса все 4 случая разные, для косинуса они парные.
Метод интервалов:
Перенести все в одну часть; записать область определения и наименьший положительный период (т.к. если функция периодическая, решать можно на одном периоде); находим нули, находим несколько корней – высчитываем их до тех пор, пока… находим нули, которые находятся на расстоянии 2П; делается рисунок, высчитываем знаки (взять любое число из промежутка и посчитать).
Какая-то книжка: ее можно отксерокопировать (там есть алгоритм) и использовать на экзамене!!
Интересное задание: неравенство, в котором синус больше 3-х или меньше единицы – не надо уметь решать неравенства тригонометрические, достаточно знать область значений.
Тема: методика изучения понятий матанализа.
Это производная, первообразная.
История.
До 1905 г. элементы матанализа в гимназиях не рассматривались (только в вузах). В 1905 г. на собрании учителей математики России был поставлен вопрос о введении теории верояностми, комбинаторики, элементов матана. В 1913 г. было поручено разрабатывать учебные пособия с включением этих тем и в 1917 перейти на эти пособия, на новые программы. Но случилась революция.
Возврат к этим идеям – во время колмогоровской реформы (конец 60-х – начало 70-х годов), в пособиях Колмогорова для всех школьников (еще не было мат классов) вышли пособия, куда были включены комбинаторика, теория вероятности, предела последовательности (по Коши и по Гейне), предела функции в точке (в двух вариантах), понятия непрерывности, производной, первообразной, опреденного интеграла для функций: степенных (корни, многочлены), рациональных, тригонометрических, показательных, логарифмических.
У учителей паника, начались сокращения материала. Сейчас осталась производная (на повышенном уровне).
В 80-е годы были исключены понятия предела последовательности, некоторые функции для дифференцирования, понятия определенного интеграла.
1996 - 2000 г. – программы Мельникова: матан исклыючен, но включены элементы комбинаторики и теории вероятности.
1998 – переход к 12-тилетней системе. Программа: Тангень: производная – для степенной функции, первообразная; комбинаторика и теория вероятностей – для повышенного и углубленного уровня.
2007 – возвращение к 11-тилетке. Сохранились элементы матана, убрали комбинаторику, теорию вероятностей, статистику.
2015 – возврат к повышенному уровню, профильные классы; матан – только на повышенном уровне.
При изучении функций в 10-11 классах появляются микросвойства – свойства, реализуемые в некоторой окрестности отдельной точки:
- точки максимума и минимума,
- максимум и минимум функции;
- непрерывность функции в точке;
- дифференцируемость;
- интегрируемость (наличие первообразной в точке).
Схема изучения производной:
1) введение определения (возможны три подхода) (методическая проблема?):
а) через понятие предела,
б) на языке «стремлений» (приближенно равно, если приращение приближенно равно)
в) на языке приближенных вычислений.
2) на основании определения вводится несколько формул дифференцирования.
3) обоснование правил дифференцирования для суммы, разности, произведения и частного функции.
Легко получаются формулы для суммы и разности, но для произведения этого уже не достаточно.
Вводится допущение: предел дельта f при дельта х стремящемся к нулю равно нулю (посмотреть, как это обосновывается, обосновывается ли).
Самое проблемное место – обоснование правила дифференцирования для произведения функции – методическая проблема.
3?) Рассмотрения физического и геометрического смысла производной.
Уравнение касательной.
Применение производной для исследования функции.
Применяется ли производная для введения новых функций.
Решение задач на наибольшее и наименьшее значение функции (изопериметрические, на максимум и минимум, на оптимизацию, на экстремум).
Проблема определений:
х0 называется точкой максимума функции f, если существует такая дельта-окрестность точки х0, что для любого х, взятого из нее, выполняется неравенство: f(x0) > f(x) (или неравенство f(x0) 
f(x)).
Непрерывность функции в точке х0:
lim f(x) = f(x0)
x→x0
1) предел функции в точке х0 существует;
2) значение функции в точке х0 существует;
3) они равны.
График см фото.
Вопросы (для кр, возможно):
1) назвать точки максимума;
2) точки, в которых ф-ция дифференцируема
3) в которых функция имеет предел;
4) в которых производная равна нулю, больше-меньше нуля.
Все понятия матана в школьном курсе рассматриваются только для двусторонних окрестностей точек (односторонние пределы не рассматриваются), т.е. для точек на концах функции (см.фото) все это не рассматривается.
1) т. максимума: х6, х4!!!, х3 – если по второму определению, х2 (там асимптоты вокруг, и в точке х2 стоит значение), промежутки (х3; х4), (х4; х5) – по второму определению;
Т. минимума: х5 – по второму определению, х7.
3) в т.х8 предела нет, на концах точки не рассматриваем; в т.х4 предел есть, но он не совпадает со значением функции в точке;
В т. х2 с точки зрения матана предел равен бесконечности, но с точки зрения школьного курса предела нет.
2) Нет производной в т. х1, х9 – по школьному курсу;
х8
в точках, где функция имеет разрыв: х2, х4;
производная существует в тех точках, где можно провести единственную касательную, т.е. в точках излома производной не существует: точки х3, х5, х7.
Графические признаки отсутствие производной:
- отсутствие двусторонней окрестности точки;
- точки разрыва;
- излом (наличие не единственной касательной).
В точке нет предела, когда точка разрыва второго рода, т.е. разрыв со скачком.
4) (х3;х4) и (х4; х5) и х6.
Методика обучения решения задач на оптимизацию.
Еще названия: на экстремум, изопериметрические, на максимум и минимум)
Проблемы:
!. Проблема первой задачи (которая разбирается с решением, на которой иллюстрируется подход)
Неудачные варианты: задача с физическим содержанием (задачи на экстремум и так сложные,а тут еще добавляются сложности физической интерпритации), стериометрические сюжеты (было неудачно, когда тема производной стояла в начале 10-го класса), сюжетные задачи из жизни (где установить вышку, с какой скоростью ехать велосипедисту, чтобы сэкономить время)
Удачные, простые примеры: связаны с площадью прямоугольника.
Например:
Задача 1. В дачнок кооперативе фрукты каждому выделяют участок прямоугольной формы площадью 10 соток. Участок нужно огородить сеткой, купленной в этом же кооперативе ценой 5$ за метр. Какие размеры должен иметь участок, чтобы цена ограждения была наименьшей.
Задача 2. В дачном кооперативе «Овощи» каждому выделяют участок прямоугольной формы с фиксированным периметром a метров. Какими должны быть размеры участка, чтобы его площадь была наибольшей.
Сравнение пособий: выделенность или невыделенность алгоритма.
Первое, что должен заметить ученик, читая условие – константы, которые есть в условии каждой задачи.
10.33 +48 = 10.33 + 27 + 21 = 11.21
| № | Константа | Выбор переменной | Название ф-ции | Формула ф-ции | Область определен. ф-ции | Способ решения |
На экзамен: вписать в табличку еще 3 задачи, стараться найти такие задачи, где трудно найти константы, трудно сделать выбор переменной, когда сложно выбрать, какую стоимость называть.
Способы решения: универсальный – исследовать производную, найти точки мах и мин; втотой – на отрезке: найти максимум, сравнить со значениями на концах.
Решение задачи 2: т.к. функция не теряет смысла при х=0 и х = g/2, можем расширить ее до отрезка и решать, используя правило Вейерштрасса.
В задаче 1 это невозможно. Ее решаем, исследуя функцию на экстремум: найти критические точки и выяснить знаки значений производной на всех образовавшихся промежутках.
В принципе, при решении задачи на оптимизацию, можно встретить области определения функции: [a; b], [a; b), (a; b), [a; +беск), (-беск.; b).
Если ограниченные интервалы можно дополнить до отрезка, можно использовать 2 подхода к решению: с использованием правила на Вейерштрасса и исследование на экстремум. В остальных случаях – только исследование на экстремум.
Если функция, составленная по условию задачи – знакомая элементарная функция (квадратичная, линейная и т.д.), то в ряде случаев можно обойтись без производной, используя графические представления и известные свойства этих функций.
1) Определение, 2) перечислить: особенности, названия, классы, виды, подходы (два подпункта), 3) два задания: первое решить обязательно, второе – для страховки.
Микросвойства – смотрим окрестность отдельной точки(непрерываность, разрывность, наличсие предела, максимум\минимума, наличие первообразной).
Простейшие неравенства: понимать, какой случай труднее (например, нестрогое неравенство сложнее – больше будет ошибок).
|
|
|
