Молекулярная физика. Термодинамика

Расчетное задание № 1

Кинематика, динамика, законы сохранения энергии.

И импульса материальной точки. Элементы теории поля.

Законы вращательного движения твердого тела.

Колебания и волны. Элементы теории относительности.

Основные формулы

 

Кинематическое уравнение движения материальной точки (центра масс твердого тела) вдоль оси x

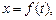
где f(t) - некоторая функция времени.

Проекция средней скорости на ось x

Средняя путевая скорость

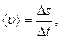
где Ds - путь, пройденный точкой за интервал времени Dt. Путь Ds в отличие от разности координат Dx = x₂-x₁не может убывать и принимать отрицательные значения, т.е. Ds ³ 0.

Проекция мгновенной скорости на ось x

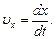
Проекция среднего ускорения на ось x

Проекция мгновенного ускорения на ось x

Кинематическое уравнение движения материальной точки по окружности

 

, r=R-const

Модуль угловой скорости

Модуль углового ускорения

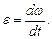
Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:

где -модуль линейной скорости; и - модули тангенциального и нормального ускорений; w - модуль угловой скорости; e - модуль углового ускорения; R -радиус окружности.

Модуль полного ускорения

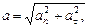или

Угол между полным 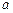и нормальным ускорениями

Импульс материальной точки массой m, движущейся со скоростью ,

.

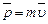Второй закон Ньютона

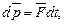
где - результирующая сила, действующая на материальную точку.

Силы, рассматриваемые в механике:

а) сила упругости

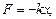
где -коэффициент упругости (в случае пружины - жесткость);

x - абсолютная деформация;

б) сила тяжести

в) сила гравитационного взаимодействия

где - гравитационная постоянная; m₁ и m₂ - массы взаимодействующих тел; r - расстояние между телами (тела рассматриваются как материальные точки). В случае гравитационного взаимодействия силу можно выразить также через напряженность гравитационного поля:

г) сила трения (скольжения)

где f - коэффициент трения; N - сила нормального давления.

Закон сохранения импульса

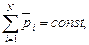
или для двух тел (i=2)

,

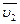где и - скорости тел в момент времени, принятый за начальный; 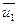и - скорости тех же тел в момент времени, принятый за конечный.

Кинетическая энергия тела, движущегося поступательно,

, или

Потенциальная энергия:

а) упругодеформированной пружины

где - жесткость пружины; x - абсолютная деформация;

б) гравитационного взаимодействия

где 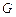- гравитационная постоянная; m₁ и m₂ - массы взаимодействующих тел; r - расстояние между ними (тела рассматриваются как материальные точки);

в) тела, находящегося в однородном поле силы тяжести,

 

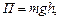
где g - ускорение свободного падения; h - высота тела над уровнем, принятым за нулевой (формула справедлива при условии h<<R, где

R — радиус Земли).

Закон сохранения механической энергии

Работа А, совершаемая результирующей силой, определяется как мера изменения кинетической энергии материальной точки:

 

 

Кинематическое уравнение гармонических колебаний материальной точки

x = A cos(wt+j),

где х - смещение; А -амплитуда колебаний; w - угловая или циклическая частота; j - начальная фаза.

Скорость и ускорение материальной точки, совершающей гармонические колебания:

u = -Aw sin (wt+j); a = - Aw² cos (wt+j).

Сложение гармонических колебаний одного направления и одинаковой частоты:

а) амплитуда результирующего колебания

б) начальная фаза результирующего колебания

Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях,

x = A₁ cos wt; y = A₂ cos (wt+j);

а) 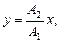если разность фаз j=0;

б) 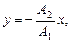если разность фаз j=±p;

в) если разность фаз j=±p/2.

Уравнение плоской бегущей волны

где y - смещение любой из точек среды с координатой x в момент t;

u - скорость распространения колебаний в среде.

Связь разности фаз Dj колебаний с расстоянием Dxмежду точками среды, отсчитанным в направлении распространения колебаний;

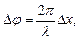
где l - длина волны.

Основное уравнение динамики вращательного движения относительно неподвижной оси z

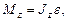
где М_z - результирующий момент внешних сил относительно оси z, действующих на тело; e - угловое ускорение; J_z - момент инерции относительно оси вращения.

Моменты инерции некоторых тел массой m относительно оси z, проходящей через центр масс:

а) стержня длиной l относительно оси, перпендикулярной стержню,

б) обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра),

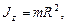
где R - радиус обруча (цилиндра);

в) диска радиусом R относительно оси, перпендикулярной плоскости диска,

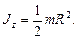
Проекция на ось z момента импульса тела, вращающегося относительно неподвижной оси z,

где w - угловая скорость тела.

Закон сохранения момента импульса систем тел, вращающихся вокруг неподвижной оси z,

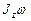= const,

где J_z - момент инерции системы тел относительно оси z; w - угловая скорость вращения тел системы вокруг оси z.

Кинетическая энергия тела, вращающегося вокруг неподвижной оси z,

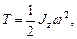или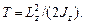

Релятивистская масса

или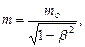

где m_o - масса покоя частицы; u - ее скорость; с - скорость света в вакууме; b - скорость частицы, выраженная в долях скорости света

(b = u/с).

Взаимосвязь массы и энергии релятивистской частицы

или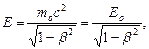

где Е_о=m_ос² - энергия покоя частицы.

Полная энергия свободной частицы

Е = Е_о + Т,

где Т - кинетическая энергия релятивистской частицы.

Кинетическая энергия релятивистской частицы

или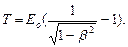

Импульс релятивистской частицы

или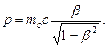

Связь между полной энергией и импульсом релятивистской частицы

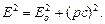
Примеры решения задач

Пример 1. Уравнение движения материальной точки вдоль оси имеет вид x = A + Bt + Ct³, где А = 2 м, В = 1 м/с, С = - 0,5 м/с³. Найти координату х, скорость 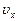и ускорение точки в момент времени t = 2с.

Решение. Координату xнайдем, подставив в уравнение движения числовые значения коэффициентов A, B и C и времени t:

x = (2 + 1×2 - 0,5×2³)м = 0.

Мгновенная скорость относительно оси хесть первая производная от координаты по времени:

.

Ускорение точки найдем, взяв первую производную от скорости по времени:

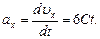
В момент времени t = 2 с

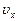= (1 - 3×0,5×2²) м/c = - 5 м/c;

= 6(- 0,5) × 2 м/с² = - 6 м/с².

 

Пример 2. Тело вращается вокруг неподвижной оси по закону j = A + Bt + Ct², где A= 10 рад, В = 20 рад/с, С = - 2 рад/с². Найти полное ускорение точки, находящейся на расстоянии г=0,1 м от оси вращения, для момента времени t =4 с.

Решение. Полное ускорение 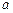точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения , направленного по касательной к траектории, и нормального ускорения , направленного к центру кривизны траектории (рис.1):

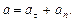
Так как векторы и взаимно перпендикулярны, то модуль ускорения

(1)

Модули тангенциального и нормального ускорения точки вращающегося тела выражаются формулами

где w - модуль угловой скорости тела; e - модуль его углового ускорения.

Подставляя выражения и в формулу (1), находим

 

 

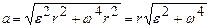. (2)

Угловую скорость w найдем, взяв первую производную угла поворота по времени:

В момент времени t = 4 с модуль угловой скорости

w = [20 + 2(-2)4] рад/с = 4 рад/с.

Угловое ускорение найдем, взяв первую производную от угловой скорости по времени:

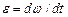= 2 C = - 4 рад/с².

Подставляя значения w, e и r в формулу (2), получаем

м/с = 1,65 м/с².

Пример 3. Шар массой m₁, движущийся горизонтально с некоторой скоростью , столкнулся с неподвижным шаром массой m₂. Шары абсолютно упругие, удар прямой, центральный. Какую долю e своей кинетической энергии первый шар передал второму?

Решение. Доля энергии, переданной первым шаром второму, выразится соотношением

(1)

где Т₁ - кинетическая энергия первого шара до удара; u₂ и Т₂ - скорость и кинетическая энергия второго шара после удара.

Как видно из формулы (1), для определения e надо найти u₂. Согласно условию задачи импульс системы двух шаров относительно горизонтального направления не изменяется и механическая энергия шаров в другие виды не переходит. Пользуясь этим, найдем:

(2)

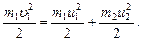(3)

Решим совместно уравнения (2) и (3):

Подставив это выражение u₂ в формулу (1) и сократив на u₁ и m₁, получим

Из найденного соотношения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров.

 

Пример 4. Через блок в виде сплошного диска, имеющего массу m= 80г (рис.2), перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами m₁ = 100г и m₂ = 200г. Определить ускорение, с которым будут двигаться грузы, если их предоставить самим себе. Трением и массой нити пренебречь.

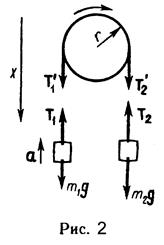
Решение: Рассмотрим силы, действующие на каждый груз и на блок в отдельности. На каждый груз действуют две силы: сила тяжести и сила упругости (сила натяжения нити). Направим ось х вертикально вниз и напишем для каждого груза уравнение движения (второй закон Ньютона) в проекциях на эту ось. Для первого груза

; (1)

для второго груза

(2)

 

Под действием моментов сил и относительно оси z перпендикулярной плоскости чертежа и направленной за чертеж, блок приобретает угловое ускорение e. Согласно основному уравнению динамики вращательного движения,

(3)

где 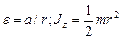- момент инерции блока (сплошного диска) относительно оси z.

Согласно третьему закону Ньютона, с учетом невесомости нити и . Воспользовавшись этим подставим в уравнение (3) вместо 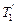и выражения и 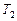_, получив их предварительно из уравнений (1) и (2):

После сокращения на и перегруппировки членов найдем

(4)

Формула (4) позволяет массы m₁, m₂ и m выразить в граммах, как они даны в условии задачи, а ускорение - в единицах СИ. После подстановки числовых значений в формулу (4) получим

 

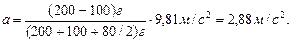
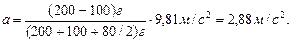
Пример 5. Ракета установлена на поверхности Земли для запуска в вертикальном направлении. При какой минимальной скорости u₁, сообщенной ракете при запуске, она удалится от поверхности на расстояние, равное радиусу Земли (R=6,37×10⁶ м)? Всеми силами, кроме силы гравитационного взаимодействия ракеты и Земли,пренебречь.

Решение. Со стороны Земли на ракету действует сила тяжести, являющаяся потенциальной силой. При неработающем двигателе под действием потенциальной силы механическая энергия ракеты изменяться не будет. Следовательно,

Т₁ + П₁ = Т₂ + П₂, (1)

где Т₁, П₁ и Т₂, П₂ - кинетическая и потенциальная энергии ракеты после выключения двигателя в начальном (у поверхности Земли) и конечном (на расстоянии, равном радиусу Земли) состояниях.

Согласно определению кинетической энергии,

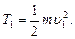
Потенциальная энергия ракеты в начальном состоянии

По мере удаления ракеты от поверхности Земли ее потенциальная энергия возрастает, а кинетическая - убывает. В конечном состоянии кинетическая энергия Т₂ станет равной нулю, а потенциальная - достигнет максимального значения:

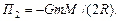
Подставляя выражения Т₁, П₁, Т₂ и П₂ в (1), получаем

откуда

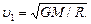
Заметив, что GM/R²=g (g - ускорение свободного падения у поверхности Земли), перепишем эту формулу в виде

что совпадает с выражением для первой космической скорости.

Произведем вычисления:

м/с = 7,9 км/с.

 

Пример 6. Платформа в виде сплошного диска радиусом R=1,5 м и массой m₁=180 кг вращается около вертикальной оси с частотой n=10 мин^-1. В центре платформы стоит человек массой m₂=60 кг. Какую линейную скорость u относительно пола помещения будет иметь человек, если он перейдет на край платформы?

Решение. Согласно условию задачи, момент внешних сил относительно оси вращения z, совпадающей с геометрической осью платформы, можно считать равным нулю. При этом условии проекция L_z момента импульса системы платформа-человек остается постоянной:

const, (1)

где J_z - момент инерции платформы с человеком относительно оси z;

w - угловая скорость платформы.

Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы, поэтому в начальном состоянии а в конечном состоянии .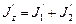

С учетом этого равенство (1) примет вид

(2)

где значения моментов инерции J₁ и J₂ платформы и человека соответственно относятся к начальному состоянию системы; 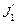и - к конечному.

Момент инерции платформы относительно оси z при переходе человека не изменяется: . Момент инерции человека относительно той же оси будет изменяться. Если рассматривать человека как материальную точку, то его момент инерции J₂ в начальном состоянии (в центре платформы)можно считать равным нулю. В конечном состоянии (на краю платформы) момент инерции человека

Подставим в формулу (2) выражения моментов инерции, начальной угловой скорости вращения платформы с человеком (w = 2pn) и конечной угловой скорости (w^' = u/R, где u - скорость человека относительно пола):

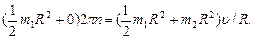
После сокращения на R² и простых преобразований находим скорость

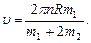
Произведем вычисления:

м/с.

 

Пример 7. Частица массой m = 0,01 кг совершает гармонические колебания с периодом Т = 2с. Полная энергия колеблющейся частицы Е = 0,1 мДж. Определить амплитуду А колебаний и наибольшее значение силы F_max, действующей на частицу.

Решение. Для определения амплитуды колебаний воспользуемся выражением полной энергии частицы:

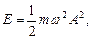
где w = 2p/Т. Отсюда амплитуда

(1)

Так как частица совершает гармонические колебания, то сила, действующая на нее, является квазиупругой и, следовательно, может быть выражена соотношением F = -kx, где k - коэффициент квазиупругой силы; х - смещение колеблющейся точки. Максимальной сила будет при максимальном смещении x_max, равном амплитуде:

F_max = kA. (2)

Коэффициент k выразим через период колебаний:

k = mw² = m×4p²/T². (3)

Подставив выражения (1) и (3) и (2) и произведя упрощения, получим

Произведем вычисления:

0,045 м = 45 мм;

 

Пример 8. Складываются два колебания одинакового направления, выраженные уравнениями

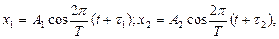
где А ₁ = 3 см, А ₂ = 2 см, t ₁ = 1/6 с, t ₂ = 1/3 с, Т = 2 с. Построить векторную диаграмму сложения этих колебаний и написать уравнение результирующего колебания.

Решение. Для построения векторной диаграммы сложения двух колебаний одного направления надо фиксировать какой-либо момент времени. Обычно векторную диаграмму строят для момента времени t = 0. Преобразовав оба уравнения к канонической форме

х = A cos (wt+j), получим

Отсюда видно, что оба складываемых гармонических колебания имеют одинаковую циклическую частоту

.

Начальные фазы первого и второго колебаний соответственно равны

Произведем вычисления:

с^-1;

 

Изобразим векторы А₁ и А₂. Для этого отложим отрезки длиной А₁ = 3 см и А₂ = 2 см под углами j₁ = 30^о и j₂ = 60^о к оси 0х. Результирующее колебание будет происходить с той же частотой w и амплитудой А, равной геометрической сумме амплитуд А₁ и А₂: А = А₁ + А₂. Согласно теореме косинусов:

Начальную фазу результирующего колебания можно также определить непосредственно из векторной диаграммы (рис. 3):

 

 

Произведем вычисления:

см = 4,84 см;

или j = 0,735 рад.

Так как результирующее колебание является гармоническим, имеет ту же частоту, что и слагаемые колебания, то его можно записать в виде

где А = 4,84 см, w = 3,14 с^-1, j = 0,735 рад.

 

Молекулярная физика. Термодинамика

Основные формулы

 

Количество вещества тела (системы)

n = N/N_A,

где N - число структурных элементов (молекул, атомов, ионов и т.п.), составляющих тело (систему); N_А - постоянная Авогадро

(N_А = 6,02×10²³моль^-1).

Молярная масса вещества

M = m/n,

где m - масса однородного тела (системы); n - количество вещества этого тела.

Относительная молекулярная масса вещества

M_r = Sn_iA_r,i,

где n_i - число атомов i-го химического элемента, входящих в состав молекулы данного вещества; A_r,i - относительная масса этого элемента. Относительные атомные массы приводятся в таблице Д.И.Менделева.

Связь молекулярной массы М с относительной молекулярной массой вещества

M = M_rk,

где k = 10^-3 кг/моль.

Количество вещества смеси газов

n = n₁ + n₂ + … + n_n = N₁/N_A + N₂/N_A + … + N_n/N_A,

или

где n_i, N_i, m_i, M_i - соответственно количество вещества, число молекул, масса, молекулярная масса i-го компонента смеси.

Уравнение Менделеева-Клайперона (уравнение состояния идеального газа)

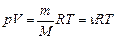
где m - масса газа, М - молекулярная масса газа, R - молекулярная газовая постоянная, n - количество вещества, Т - термодинамическая температура.

Опытные газовые законы, являющиеся частными случаями уравнения Менделеева-Клайперона для изопроцессов:

а) закон Бойля-Мариотта (изотермический процесс: T=const, m=const)

pV = const,

или для двух состояний газа

p₁V₁ = p₂V₂;

б) закон Гей-Люссака (изобарный процесс: p=const, m=const)

или для двух состояний

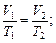
в) закон Шарля (изохорный процесс: V=const, m=const)

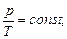
или для двух состояний

г) объединенный газовый закон (m=const)

или

где p₁,V₁,T₁ - давление, объем и температура газа в начальном состоянии; p₂,V₂,T₂ - те же величины в конечном состоянии.

Закон Дальтона, определяющий давление смеси газов,

р = р₁ + р₂ + … + р_n

где p_i - парциальные давления компонентов смеси; n - число компонентов смеси.

Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.

Молекулярная масса смеси газов

где m_i - масса i-го компонента смеси; ni = m_i/M_i - количество вещества i-го компонента смеси; n - число компонентов смеси.

Массовая доля i-го компонента смеси газа (в долях единицы или процентах)

где m - масса смеси.

Концентрация молекул

где N - число молекул, содержащихся в данной системе; r - плотность вещества; V - объем системы. Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.

Основное уравнение кинетической теории газов

p = 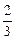n áe_пñ,

где áe_пñ - средняя кинетическая энергия поступательного движения молекулы.

Средняя кинетическая энергия поступательного движения молекулы

áe_пñ = kT,

где k - постоянная Больцмана.

Средняя полная кинетическая энергия молекулы

áe_iñ = 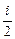kT,

где i - число степеней свободы молекулы.

Зависимость давления газа от концентрации молекул и температуры

p = nkT.

Скорости молекул:

- средняя квадратичная;

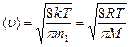- средняя арифметическая;

- наиболее вероятная,

где m_i - масса одной молекулы.

Относительная скорость молекулы

u = u/u_B,

где u - скорость данной молекулы.

Удельные теплоемкости газа при постоянном объеме (с_v) и постоянном давлении (c_p)

Связь между удельной с и молекулярной С теплоемкостями

с = С/М, С = сМ.

Уравнение Майера

С_p – C_v = R

Внутренняя энергия идеального газа

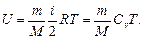
Первое начало термодинамики

где Q - теплота, сообщенная системе (газу); DU - изменение внутренней энергии системы; А - работа, совершенная системой против внешних сил.

Работа расширения газа:

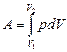в общем случае;

A = p(V₂-V₁) при изобарном процессе;

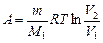при изотермическом процессе;

, или

при адиабатном процессе, где g = с_p/c_v - показатель адиабаты.

Уравнения Пуассона, связывающие параметры идеального газа при адиабатном процессе:

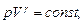
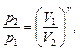
Термический КПД цикла

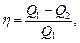
где Q₁ - теплота, полученная рабочим телом от теплоотдатчика; Q₂ - теплота, переданная рабочим телом теплоприемнику.

Термический КПД цикла Карно

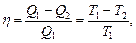
где T₁ и T₂ - термодинамические температуры теплоотдатчика и теплоприемника.

Коэффициент поверхностного натяжения

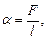или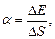

где F - сила поверхностного натяжения, действующая на контур l, ограничивающий поверхность жидкости; DЕ - изменение свободной энергии поверхностной пленки жидкости, связанное с изменением площади DS поверхности этой пленки.

Формула Лапласа, выражающая давление р, создаваемое сферической поверхностью жидкости:

где R - радиус сферической поверхности.

Высота подъема жидкости в капиллярной трубке

где q - краевой угол (q = 0 при полном смачивании стенок трубки жидкостью; q = p при полном несмачивании); R - радиус канала трубки; r - плотность жидкости; g - ускорение свободного падения.

Высота подъема жидкости между двумя близкими параллельными друг другу плоскостями

где d - расстояние между плоскостями.

 

Примеры решения задач

 

Пример 1. Определить молярную массу М смеси кислорода массой 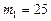г и азота массой г.

Решение. Молярная масса смеси М есть отношение массы смеси m к количеству вещества смеси :

. (1)

Масса смеси равна сумме масс компонентов смеси:

.

Количество вещества смеси равно сумме количеств вещества компонентов:

.

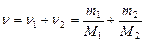Подставив в формулу (1) выражения и , получим

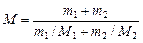. (2)

Найдем молярные массы кислорода 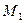и азота :

кг/моль; кг/моль.

Подставим значения величин в (2) и произведем вычисления:

кг/моль =

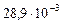= кг/моль.

 

Пример 2. Найти среднюю кинетическую энергию вращательного движения одной молекулы кислорода при температуре К, а также кинетическую энергию 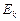вращательного движения всех молекул кислорода массой г.

Решение. На каждую степень свободы молекулы газа приходится одинаковая средняя энергия , где k – постоянная Больцмана; T – термодинамическая температура газа. Так как вращательному движению двухатомной молекулы (молекула кислорода – двухатомная) соответствуют две степени свободы, то средняя энергия вращательного движения молекулы кислорода

. (1)

Кинетическая энергия вращательного движения всех молекул газа

. (2)

Число всех молекул газа

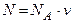, (3)

где 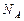– постоянная Авогадро; – количество вещества.

Если учесть, что количество вещества , где m – масса газа; М – молярная масса газа, то формула (3) примет вид

.

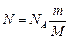Подставив выражение N в формулу (2), получаем

. (4)

Произведем вычисления, учитывая, что для кислорода кг/моль:

Дж Дж;

Дж Дж.

 

Пример 3. Вычислить удельные теплоемкости и смеси неона и водорода, если массовые доли неона и водорода составляют 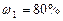и 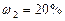. Значения удельных теплоемкостей газов взять из справочника.

Решение. Удельную теплоемкость смеси при постоянном объеме найдем следующим образом. Теплоту, необходимую для нагревания смеси на , выразим двумя способами:

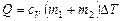, (1)

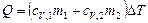, (2)

где – удельная теплоемкость неона; 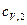– удельная теплоемкость водорода.

Приравняв правые части (1) и (2) и разделив обе части полученного равенства на , получим . Отсюда

,

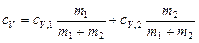или

,

где и