 |
Комбинаторные конфигурации
|
|
|
|
Во многих практических случаях возникает необходимость подсчитать количество возможных комбинаций объектов, удовлетворяющих определенным условиям. Такие задачи называются комбинаторными. Разнообразие комбинаторных задач не поддается исчерпывающему описанию, но среди них есть целый ряд особенно часто встречающихся, для которых известны способы подсчета.
Комбинаторные задачи
Для формулировки и решения комбинаторных задач используются различные модели комбинаторных конфигураций. Рассмотрим следующие две наиболее популярные.
1. Дано n предметов. Их нужно разместить по m ящикам так, чтобы выполнялись заданные ограничения. Сколькими способами это можно сделать?
2. Рассмотрим множество функций
F:X→Y, где |X|=n, |Y|=m, X={1,...,n}.
Не ограничивая общности, можно считать, что
Y={1,...m}, F=‹F(1),...,F(n)›, 1≤F(i)≤m.
Сколько существует функций F, удовлетворяющих заданным ограничениям?
Замечание!
Большей частью соответствие конфигураций, описанных на «языке ящиков» и «языке функций», очевидно, поэтому доказательство правильности способа подсчета (вывод формулы) можно провести на любом языке. Если сведение одной модели к другой не очевидно, то оно включается в доказательство.
Размещения
Число всех функций (при отсутствии ограничений), или число всех возможных способов разместить n предметов по m ящикам, называется числом размещений и обозначается U(m,n).
Теорема: U(m,n)=mn.
Доказательство:
Каждый из n предметов можно разместить m способами.
Пример.
При игре в кости бросаются две кости и выпавшие на верхних гранях очки складываются. Какова вероятность выбросить 12 очков? Каждый возможный исход соответствует функции F:{1,2}→{1,2,3,4,5,6} (аргумент – номер кости, результат – очки на верхней грани).
|
|
|
Таким образом, всего возможно U(6,2)=62=36 различных исходов. Из них только один (6+6) дает двенадцать очков. Вероятность 1/36.
Размещения без повторений
Число инъективных функций, или число всех возможных способов разместить n предметов по m ящикам, не более чем по одному в ящик, называется числом размещений без повторений и обозначается A(m,n) или [m]n, или (m)n.
 |
Теорема: A(m,n)=
Доказательство:
Ящик для первого предмета можно выбрать m способами, для второго - (m-1) способами, и так далее. Таким образом,
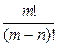 |
A(m,n)=m*(m-1)*...*(m-n+1)=
По определению считают, что A(m,n)=0 при n>m и A(m,0)=1.
Пример:
В некоторых видах спортивных соревнований исходом является определение участников, занявших первое, второе и третье места. Сколько возможно различных исходов, если в соревновании участвуют n участников? Каждый возможный исход соответствует функции F: {1,2,3}→{1..n} (аргумент – номер призового места, результат – номер участника). Таким образом, всего возможно A(n,3)=n*(n-1)*(n-2) различных исходов.
Перестановки
Число взаимнооднозначных функций, или число перестановок n предметов, обозначается P(n).
Теорема: P(n)=n!
Доказательство:
P(n) = A(n,n) = n*(n-1)*...*(n-n+1) = n*(n-1)*...*1 = n!
Пример:
Сколькими способами 6 человек могут сесть на 6 стульев?
Пронумеруем стулья числами 1,2,3,4,5,6 и обозначим человека, севшего на k-стул, через. Тогда – перестановка из имен этих 6-и людей, причем каждой такой перестановке соответствует один и только один способ размещения на стульях. Значит, число способов равно P6=6!=720.
Пример: Секретные замки
Для запирания сейфов и автоматических камер хранения багажа применяют секретные замки, которые открываются лишь тогда, когда набрано «тайное слово» (или тайный набор цифр). Это слово набирают с помощью одного или нескольких дисков, на которых изображены буквы (или цифры). Пусть число букв на каждом диске равно 12, а число дисков равно 5. Сколько неудачных попыток может быть сделано человеком, не знающим секретного слова и подбирающим его наудачу?
|
|
|
Из условия задачи видно, что порядок выбираемых букв существен (одно дело набрать на первом диске букву «а», а на втором букву «б», а другое — набрать эти же буквы в обратном порядке). Поэтому мы имеем здесь дело с кортежами. При этом никаких ограничений на эти кортежи не наложено.
Так как по условию каждая буква может быть выбрана 12 способами, а длина кортежей равна 5, то получаем, что число комбинаций равно 125 = 248 832. Значит, неудачных попыток может быть 248 831. Считая по 10 секунд на одну попытку, получаем, что для открытия сейфа понадобится более 340 часов непрерывной работы. Впрочем, обычно сейфы делают так, чтобы после первой же неудачной попытки раздавался сигнал тревоги.
Сочетания
Число строго монотонных функций, или число размещений n неразличимых предметов по m ящикам, не более чем по одному в ящик, то есть число способов выбрать из m ящиков n ящиков с предметами, называется числом сочетаний и обозначается C(m,n) или Cnm или (nm).
 |
Теорема: C(m,n)=
Пример:
В начале игры в домино каждому играющему выдается 7 костей из имеющихся 28 различных костей. Сколько существует различных комбинаций костей, которые игрок может получить в начале игры? Очевидно, что искомое число равно числу 7-элементных подмножеств 28-элементного множества. Имеем:
 |
С(28,7)=
=1184040.
Сочетания с повторениями
Число монотонных функций, или число размещений n неразличимых предметов по m ящикам, называется числом сочетаний с повторениями и обозначается V(m,n).
Теорема:
V(m,n)=C(m+n-1,n).
Пример:
Сколькими способами можно рассадить вновь прибывших гостей среди гостей, уже сидящих за круглым столом? Очевидно, что между сидящими за круглым столом гостями имеется промежутков, в которые можно рассаживать вновь прибывших.
Таким образом, это можно сделать
 |
V(m,n)=C(m+n-1,n)=
способами.
|
|
|


