Некоторые основные физические постоянные

Министерство образования и науки Украины

Донецкий национальный технический университет

 

 

Методические указания

и индивидуальные задания по общему курсу физики

(раздел,,Электростатика и постоянный ток ”)

 

.

 

Утверждено

на заседании кафедры физики

Протокол №9 от 06.04.2006 г.

 

Утверждено

на заседании учебно

издательского совета

Протокол №1 от.15.03.2006г.

 

 

 

 

УДК 53(071)

 

”Методические указания и индивидуальные задания по общему курсу физики (раздел ”Электростатика и постоянный ток”) ”.

Авторы: Волынская В.Г., Малышева С.В., Савченко Т.А.

Донецк: ДонНТУ, 2006 -37 с.

 

Пособие включает 100 задач, которые полностью охватывают материалы программы по общему курсу физики (раздел ”Электростатика и постоянный ток”). Методическое пособие состоит из трех частей. В первой части приводятся основные понятия, законы и формулы. Вторая часть содержит примеры решения задач и задачи для самостоятельной работы, третья часть – приложения.

Основное назначения пособия – оказать помощь студентам инженерно-технических специальностей ДонНТУ в изучении курса физики (раздел ”Электростатика и постоянный ток”).

 

Составители: Волынская В.Г.

Савченко Т.А.

Малышева С.В.

 

 

Ответственный за выпуск Гольцов В.А., профессор

Рецензент Ветчинов А.В., доцент

 

Электростатика и постоянный ток

Основные законы и формулы

§ Закон Кулона

где F – cила взаимодействия двух точечных зарядов Q₁ и Q₂ в вакууме; r – расстояние между зарядами; e₀ – электрическая постоянная, равная 8,85*10^-12 Ф/м

§ Напряженность и потенциал электрстатического поля

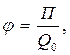или

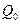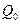где – сила, действующая на точечный положительный заряд , помещенный в данную точку поля; – потенциальная энергия заряда ; – работа перемещения заряда 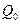из данной точки поля за его пределы.

§ Напряженность и потенциал электростатического поля точечного заряда Q на расстоянии r от заряда.

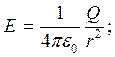
§ Поток вектора напряженности через площадку dS

где – вектор, модуль которого равен , а направление совпалает с нормалью к площадке; 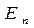– составляющая вектора по направлению нормали к площадке.

§ Поток вектора напряженности через произвольную поверхность S.

§ Принцип суперпозиции (наложения) электростатических полей.

где , 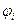– соответственно напряженность и потенциал поля, создаваемого зарядом .

§ Связь между напряженностью и потенциалом электростатического поля

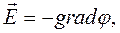или

где , , 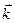– единичные векторы координатных осей.

§ В случае поля, обладающего центральной или осевой симметрией,

§ Электрический момент диполя (дипольный момент)

где – плечо диполя.

§ Плотность зарядов линейная, поверхностная и объемная, т.е. заряд, приходящийся соответственно на единицу длины, поверхности и объема:

§ Теорема Гаусса для электростатического поля в вакууме

где – электрическая постоянная; –алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности S; n – число зарядов; r – объемная плотность зарядов.

§ Напряженность поля, создаваемого равномерно заряженной бесконечной плоскостью,

§ Напряженность поля, создаваемого двумя бесконечными параллельными разноименно заряженными плоскостями,

§ Напряженность поля, создаваемого равномерно заряженной сферической поверхностью радиусом R с общим зарядом Q на расстоянии r от центра сферы,

при r < R (внутри сферы);

при (вне сферы).

§ Напряженность поля, создаваемого объемно заряженным шаром радиусом R с общим зарядом Q на расстоянии r от центра шара,

при (внутри шара);

при (вне шара).

§ Напряженность поля, создаваемого равномерно заряженным бесконечным цилиндром радиусом R на расстоянии r от оси цилиндра,

при r < R (внутри цилиндра);

при (вне цилиндра).

§ Циркуляция вектора напряженности электростатического поля вдоль замкнутого контура

где – проекция вектора 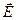на направление элементарного перемещения . Интегрирование производится по любому замкнутому пути L.

§ Работа, совершаемая силами электростатического поля при перемещении заряда Q₀ из точки 1 в точку 2,

или

где – проекция вектора 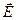на направление элементарного перемещения .

§ Поляризованность

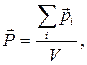
где V – объем диэлектрика; – дипольный момент i-й молекулы.

§ Связь между поляризованностью диэлектрика и напряженностью электростатического поля

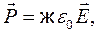
где – диэлектрическая восприимчивость вещества.

§ Связь диэлектрической проницаемости с диэлектрической восприимчивостью

§ Связь между напряженностью Е поля в диэлектрике и напряженностью Е₀ внешнего поля

или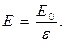

§ Связь между векторами электрического смещения и напряженностью электростатического поля

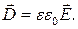
§ Связь между 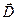, 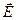и

§ Электроемкость уединенного проводника

где Q – заряд, сообщенный проводнику; 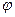– потенциал проводника.

§ Электроемкость плоского конденсатора

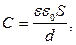
где S – площадь каждой пластины конденсатора; d – расстояние между пластинами.

§

§ Электроемкость цилиндрического конденсатора

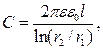
где l – длина обкладок конденсатора; r₁ и r₂ – радиусы полых коаксиальных цилиндров.

§ Электроемкость сферического конденсатора

где r₁ и r₂ – радиусы концентрических сфер.

§ Электроемкость системы конденсаторов соответственно при последовательном и параллельном соединении

и

где – электроемкость i-го конденсатора; n – число конденсаторов.

§ Энергия уединенного заряженного проводника

§ Энергия взаимодействия системы точечных зарядов

где 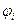– потенциал, создаваемый в той точке, где находится заряд Q_i, всеми зарядами, кроме i-го.

§ Энергия заряженного конденсатора

где Q – заряд конденсатора; С – его емкость; – разность потенциалов между обкладками.

§ Сила притяжения между двумя разноименно заряженными обкладками конденсатора

§ Энергия электростатического поля плоского конденсатора

§ Сила и плотность электрического тока

где S – площадь поперечного сечения проводника.

§ Плотность тока в проводнике

где – скорость упорядоченного движения зарядов в проводнике; n – концентрация зарядов.

§ Электродвижущая сила, действующая в цепи,

или

где Q₀ – единичный положительный заряд; А – работа сторонних сил; – напряженность поля сторонних сил.

§ Сопротивление R однородного линейного проводника, проводимость G проводника и удельная электрическая проводимость g вещества проводника соответственно равны

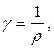
где r – удельное электрическое сопротивление; S – площадь поперечного сечения проводника; l – его длина.

§ Сопротивление проводников при последовательном соединении

при параллельном соединении

где R_i – сопротивление i-го проводника; n – число проводников.

§ Зависимость удельного сопротивления r материала проводника от его температуры

где – температурный коэффициент сопротивления.

§ Закон Ома:

для однородного участка цепи

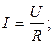
для неоднородного участка цепи

для замкнутой цепи

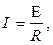
где U – напряжение на участке цепи; R – сопротивление цепи (участка цепи); – разность потенциалов на концах участка цепи; – ЭДС источников тока, входящих в участок; – ЭДС всех источников тока цепи.

§ Закон Ома в дифференциальной форме

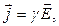
где 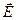– напряженность электростатического поля.

§ Работа тока за время t

§ Мощность тока

§ Закон Джоуля-Ленца

где Q – количество теплоты, выделяющееся в участке цепи за время t при прохождении тока.

§ Закон Джоуля-Ленца в дифференциальной форме

где w – удельная тепловая мощность тока, Е – напряженность электрического поля.

§ Правила Кирхгофа

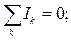
где 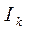– ток в k-том проводнике; и – ток и сопротивление соответственно на i-ом участке контура; – алгебраическая сумма ЭДС, что действуют в k-ом контуре.

 

Примеры решения задач.

Пример1. Плоский конденсатор площадью пластин S и стеклянной пластинкой толщиной d заряжен до разности потенциалов U и отключен от источника напряжения. Какую работу нужно совершить, чтобы вынуть пластинку из конденсатора?

 

Дано: S,d,U,ε

Определить А.

Решение. Работу по удалению пластинки из конденсатора находим как разность начальной и конечной энергии заряженного конденсатора.

где - энергия конденсатора после удаления пластинки; - энергия конденсатора до удаления пластинки.

Поскольку конденсатор отсоединен от источника напряжения, то заряд останется прежним.

Выразим энергию конденсатора и через заряд и емкость:

 

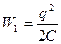
Тогда 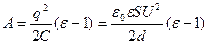т.к. , где ε – диэлектрическая проницаемость стекла.

Проверим единицы измерения А:

 

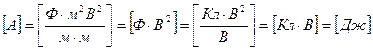
Ответ:

 

Пример 2. Генератор с ЭДС ε=140 В и внутренним сопротивлением r=0,2 Ом дает ток I=100А. Сопротивление внешней цепи R=1,2 Ом. Определить полную и полезную мощность генератора, потери мощности и КПД. Составить уравнения баланса мощностей.

 

Дано: ε=140 В, r=0.2 Ом, I=100A, R=1,2 Ом

Определить: , P, ΔP и КПД

Решение. Полная мощность генератора:

(1)

где I – сила тока; ε – ЭДС.

Полезная мощость:

(2)

где U – разность потенциалов на концах цепи.

Учитывая, что

(3)

где r – внутреннее сопротивление источника тока

Имеем:

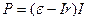(4)

Потери мощности во внешней цепи

(5)

 

КПД:

(6)

 

Проверим единицы измерения искомых величин:

 

 

Подставляя в (1,4,5 и 6) числовые значения и вычисляя получим:

 

Вт=14 (кВт)

(Вт)=12 (кВт)

ΔP=14-12=2 (кВт)

 

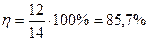
Проверим уравнение баланса мощностей:

 

Ответ: = 14 кВт; P = 12 кВт; ΔP=2 кВт; η=85,7%

 

Пример3. Сила тока в проводнике сопротивлением R=50 Ом равномерно растет от =0 до =3А за время τ=6 c. Определить выделившееся в проводнике за это время количество теплоты.

 

Дано: R=50 Ом, , , τ=6 c

Определить Q.

Решение. Согласно закону Джоуля-Ленца в случае бесконечного промежутка времени

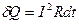
По условию задачи сила тока равномерно растет, т.е.

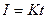
где коэффициент пропорциональности

 

Тогда можно записать:

(1)

 

После интегрирования (1) с учетом выражения для K получим:

 

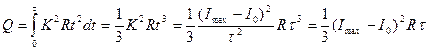(2)

 

Проверим единицы измерения Q:

 

 

Подставив в (2) числовые значения и вычисляя получим:

 

Ответ: Q=900 Дж

 

Пример4. Плотность электрического тока в медном проводе равна 10 . Определить удельную тепловую мощность тока, если удельное сопротивление меди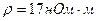

 

Дано: ,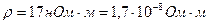

Определить ω.

Решение. Согласно законам Джоуля-Ленца и Ома в дифференциальной форме,

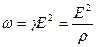(1)

(2)

где γ и ρ – соответственно удельные проводимость и сопротивление проводника;

E – напряженность электрического поля;

ω – удельная тепловая мощность тока.

 

Из закона (2) получим, что E= ρ γ. Подставив это выражение в (1), найдем искомую величину тепловой мощности тока.

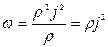(3)

Проверим единицы измерения ω:

[ω] =

 

Подставив в (3) числовые значения и вычисляя получим:

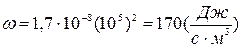
Ответ: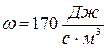

 

Пример 5. Между обкладками плоского конденсатора, заряженного до разности потенциалов 1,5 кВ, зажата парафиновая пластинка (ε=2) толщиной 5 мм.

Определить поверхностную плотность связанных зарядов на парафине.

 

Дано: U=1,5кВ=1,5 В; ε=2; d = 5мм = м.

Определить .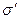

Решение. Так как векторы и нормальные к поверхности диэлектрика, то ; ; Тогда можно записать

(1)

Где и соответственно векторы электрического смещения и напряженности поля плоского конденсатора;

- вектор поляризованности диэлектрика. P = 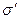, т.е. равен поверхностной плотности связанных зарядов диэлектрика.

Тогда Отсюда

(2)

Учитывая, что и , где d – расстояние между обкладками конденсатора, получим:

(3)

Проверим единицы измерения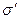

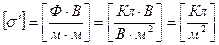
Подставив в (3) числовые значения и вычисляя получим:

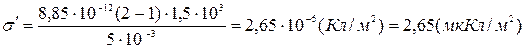
Ответ:

 

Пример 6. Расстояние l между двумя точечными зарядами 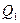=1нКл и =-2нКл, расположенными в вакууме, равно 10 см. Определить:

1) Напряженность E;

2) Потенциал φ поля, создаваемого этими зарядами в точке А, удаленной от первого заряда на расстояние = 9 см. и от второго заряда на 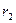=7 см.

Дано: l=10 см = 0.1 м; 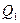=1нКл= Кл; =-2нКл= Кл;

= 9 см=0,09 м; 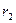=7 см.=0,07 м.

Определить: 1)Е; 2) φ;

 

Решение. Согласно принципу суперпозиции . Направления векторов указаны на рис.1. Модуль вектора найдем по теореме косинусов:

 

 

 

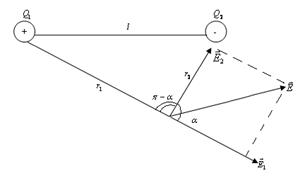
(1)

Где (2)

 

 

Рис.1

 

 

В данном случае во избежание громоздких записей удобно значение cos α вычислить отдельно:

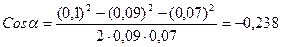(3)

 

Напряженности электрического поля, создаваемые в вакууме зарядами 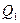и :

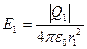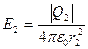, (4)

 

Подставив (4) и (3) в формулу (1), получим искомую напряженность:

 

(5)

 

Согласно принципу суперпозиции, потенциал результирующего поля

(6)

где и - потенциалы полей создаваемых соответственно

зарядам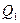и и .

Тогда (7)

Проверим единицы измерения Е и φ.

 

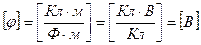
Подставив в (5) и (7) числовые значения и вычисляя получим:

Ответ: E=3,57 кВ/м, φ=-157 В

 

Пример 7.Две концентрические проводящие сферы радиусами R₁=6 см и R₂=10 см несут соответственно заряды Q₁=1 нКл и Q₂=-0.5 нКл. Найти напряженность поля в точках, отстоящих от центра сфер на расстояниях r₁=5 см, r₂=9 см и r₃=15 см. Построить график E(r).

Дано: R₁=0.06 м, R₂=0.1 м, Q₁=10^-9 Кл, Q₂=-5*10^-10 Кл, r₁=5*10^{-2 м}, r₂=9*10^{-2 м}, r₃=15*10^{-2 см}.

Е₁–?,

Е₂–?, Е₃–?, Е(r)–?

1. Для определения напряженности Е₁ проведем гауссовую поверхность S₁ радиусом r_1, рис. 2 и воспользуемся теоремой Остроградского-Гаусса:

 

(т.к. суммарный заряд, находящийся внутри гауссовой поверхности, равен нулю).

Рис.2

Следовательно, и Е₁ во всех точках, удовлетворяющих условию r₁<R₁, будет равна нулю.

2. Проведем гауссовую поверхность радиусом r₂

(так как внутри гауссовой поверхности находится только заряд Q₁)

Из соображений симметрии E_n=E₂=const, то Е₂ можно вынести за знак интеграла:

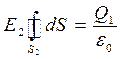или

, где – площадь гауссовой поверхности.

3. Проведем гауссовую поверхность радиусом r₃

(так как внутри гауссовой поверхности находятся заряды Q₁ и Q₂)

– площадь гауссовой поверхности

Получим:

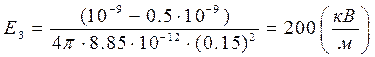
Построим график E(r),рис.3

1) r<R₁,

2) r=R,

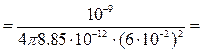
. E₂(r) изменяется

Рис.3 по закону .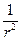

r=R₂;

3) r=R₂;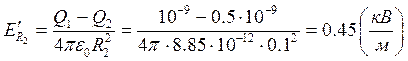

 

Таким образом, функция E(r) в точках r=R₁ и r=R₂ терпит разрыв.

Ответ: Е₁=0, Е₂=1.11 , Е₃=200 .

 

Пример8. На расстоянии =4 см от бесконечно длинной заряженной нити находится точечный заряд q=0,66 нКл. Под действием поля заряд приближается к нити до расстояния 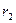=2 см. При этом совершается работа 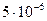Дж. Найти линейную плотность заряда на нити.

Дано: =4см= м; 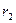=2 см= 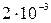м; q=0,66нКл; А= 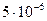Дж

Определить: τ

Решение. Работа, совершаемая силами элекrтрического поля при перемещении заряда

где dU=-E dr;

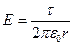- напряженность поля бесконечно длинной заряженной нити.

Тогда

Проинтегрировав это выражение получим:

Отсюда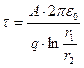

Проверим единицы измерения τ:

 

Подставив числовые значения и вычисляя получим:

 

Ответ:

.

Пример 9. На тонком стержне длинной l= 20 см находится равномерно распределенный электрический заряд. На продолжении оси стержня на расстоянии а= 10 см от ближайшего конца находиться точечный заряд Q1 =40 нКл, который взаимодействует со стержнем с силой F= 6 мкН. Определить линейную плотность заряда на стержне.

 

Дано: l=0,2 м, а=0,1 м, Q1=40нКл=4 Кл

Определить: τ.

Решение. Согласно закону Кулона сила взаимодействия двух точечных зарядов

 

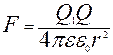
Где ε =1 – диэлектрическая проницаемость среды,

ε -электрическая постоянная,

r - расстояние между зарядами.

 

Т.к. заряд на стержне не является точечным, поэтому на стержне рис.4 выделим малый участок dr c зарядом dQ= τ dr, где τ - линейная плотность заряда на стержне.

 

Получим:

dr r

Q1

l a

Рис. 4

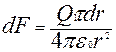
Интегрируя это выражение в пределах от а до а+l, получаем

Откуда:

Проверим единицы измеренияй:

Подставив числовые значения и вычисляя, получим:

Ответ: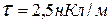

 

Пример 10. Определить силу тока, текущего через элемент ε , если ε = 1 В,

ε = 2 В, ε = 3 В, r = 1 Ом, r = 0.5 Ом, r = 1/3 Ом, R = 1 Ом, R = 1/3 Ом.

Дано: ε = 1 В, ε = 2 В, ε = 3 В, r = 1 Ом, r = 0.5 Ом, r = 1/3 Ом, R = 1 Ом, R = 1/3 Ом. Определить I .

Выберем произвольно направления токов в ветвях (см. рис.5). К решению задачи применим законы Кирхгоффа. По первому закону Кирхгоффа для узла А имеем: – I + I + I = 0 (1) Недостающие уравнения со- ставляем по второму закону Кирхгоффа. В данной схеме три контура: ABCA, ACDA, ABCDA. Выберем направление обхода кон-

I ε , r

B C

 

 

ε , r I

R I ε , r

 

А R Д

Рис.5

 

для контура ABCA

– I r – I R – I r = ε – ε (2)

для контура ADCA

I r – I R – I r = ε – ε (3)

Подставив в (2) и (3) числовые значения сопротивлений и ЭДС получим систему уравнений:

I = I + I (4)

2 I +0.5 I = 1 (5)

– 0.5 I +2/3 I = 1(6)

Из (4) и (5) следует

0.5I + 2I + 2I = 1. Отсюда

I = (7)

Из (6) и (7) находим I .

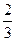
– 0.5 I + =1 или

– 1.5 I + 1 – 2.5 I = 3

Отсюда I = – (А)

Знак минус у числового значения силы тока I свидетельствует о том, что при произвольном выборе направлений токов, указанных на рис.5, направление тока I было указано противоположно истинному. На самом деле ток I течет от узла A к С.

Ответ: I = – A.

 

 

Задачи

 

3.1. Сила гравитационного притяжения двух водяных одинаково заряженных капель радиусами 0,1 м

Поделиться:

Воспользуйтесь поиском по сайту: