 |
Тест 6. Угол между плоскостями.
|
|
|
|
Тест 5. Перпендикуляр и наклонные.
Вариант 1.
Выбери верный ответ.
1. Из точки М к плоскости α проведены две наклонные, длины которых 20см и 15см. Их проекции на эту плоскость относятся как 16: 9 (рис. 1 ). Найдите расстояние от точки М до плоскости α.
а) 20см; б) 6  см; в) 13см; г) 12см.
см; в) 13см; г) 12см.
Рис. 1
М

О А
С

2. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4см (рис. 2). Найдите расстояние от точки M до плоскости ABC, если AB = 6см.
а) 4см; б) 8см; в) 6см; г) 2см.
 Рис.2
Рис.2
М
А В
О
С
3. Через точку А, удаленную от плоскости α на 4см, проходит прямая, пересекающая плоскость α в точке В. Найдите угол между прямой АВ и плоскостью α, если длина отрезка АВ равна 6см.
а) arccos2/3; б) arcsin2/3; в) arcsin3/2; г) arctg2/3.
Точка М не лежащая в плоскости треугольника АВС равноудалена от его вершин, МО – перпендикуляр к плоскости АВС. Точка О является
а) центром вписанной в треугольник АВС окружности;
б) центром описанной возле треугольника АВС окружности;
в) центром тяжести треугольника АВС;
г) точкой пересечения высот треугольника АВС.
5. Отрезок КА – перпендикуляр к плоскости квадрата АВСД, площадь которого 36 см 2 (рис. 3). Расстояние между прямыми КА и ВС равно
а) 6  см; б) 12 см; в) определить нельзя, не хватает данных; г) 6 см.
см; б) 12 см; в) определить нельзя, не хватает данных; г) 6 см.
 К Рис. 3
К Рис. 3
А В
Д С
6. Отрезок НВ перпендикулярен плоскости квадрата АВСД (рис. 4). Угол между прямой НД и плоскостью квадрата АВСД это угол
а) НВД; б) НДС; в) НДВ; г) НДА.
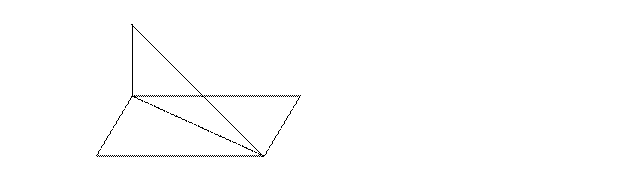 Н Рис. 4
Н Рис. 4
В С
А Д
7. Прямая CD перпендикулярна к плоскости остроугольного треугольника ABC, у которого CK – высота (рис. 5). Найдите расстояние от точки A до плоскости CDK, если DA = 8 см, а  DAK = 450.
DAK = 450.
|
|
|
а) 4 см; б) 2  см; в)
см; в)  см; г) 16см.
см; г) 16см.
 Д Рис. 5
Д Рис. 5
 |
С А
 |
В К
8. ВВ1 – перпендикуляр к плоскости ромба АВСД, диагонали которого пересекаются в точке О (рис. 6). Плоскости В1ОВ перпендикулярна прямая а) АВ; б) ВС; в) СД; г) АС.

 В1 Рис. 6
В1 Рис. 6




 В С
В С
О
 А Д
А Д
Тест 5. Перпендикуляр и наклонные.
Вариант 2.
Выбери верный ответ.
1. Из точки М к плоскости α проведены две наклонные (рис. 1), длины которых относятся как 13: 15. Их проекции на эту плоскость равны 10 см и 18 см. Найдите расстояние от точки М до плоскости α.
а) 34см; б) 24см; в) 32см; г) 23см.
 М Рис. 1
М Рис. 1
О К
Д
2. Расстояние от точки К до каждой из вершин квадрата ABCD равно 5см (рис.2) Найдите расстояние от точки K до плоскости ABC, если AB =3  см.
см.
а) 4 см; б) 4  см; в) 2см; г)
см; в) 2см; г) 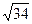 см.
см.
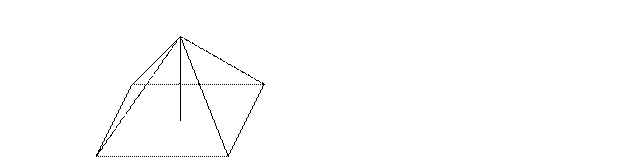 К Рис. 2
К Рис. 2
А В
Н
С Д
3. Через точку А, удаленную от плоскости α на 3см, проходит прямая, пересекающая плоскость α в точке В. Угол между прямой АВ и плоскостью α равен 30 0. Найдите длину отрезка АВ.
а)4см; б)3см; в)6см; г)5см.
Точка М не лежащая в плоскости треугольника АВС равноудалена от его сторон, МО – перпендикуляр к плоскости АВС. Точка О является
а) центром вписанной в треугольник АВС окружности;
б) центром описанной возле треугольника АВС окружности;
в) центром тяжести треугольника АВС;
г) точкой пересечения высот треугольника АВС.
5. Отрезок МВ – перпендикуляр к плоскости квадрата АВСД, площадь которого 64 см 2 (рис. 3). Расстояние между прямыми МВ и СД равно
а) 8  см; б) 16 см; в) определить нельзя, не хватает данных; г) 8 см.
см; б) 16 см; в) определить нельзя, не хватает данных; г) 8 см.

М Рис. 3
В С
А Д
6. Отрезок КА перпендикуляр к плоскости треугольника АВС. АН – высота этого треугольника (рис. 4). Углом между прямой КН и плоскостью АВС является угол
а) КНВ; б) КНС; в) КАН; г) КНА.
К Рис. 4

А В
Н
С
7. Отрезок ВМ – перпендикуляр к плоскости равнобедренного треугольника АВС, АВ = ВС = 5 см и ВК = 4см. ВК – медиана треугольника АВС (рис. 5). Найдите расстояние от точки С до плоскости МВК а) 2 см; б) 3 см; в) 4 см; г) 5 см.
|
|
|
М Рис.5





В С
К
А
8. СС1 – перпендикуляр к плоскости квадрата АВСД, диагонали которого пересекаются в точке О (рис. 6). Плоскости С1ОС перпендикулярна прямая а) СД; б) ВС; в) ОД; г) АД.







 С1 Рис.6
С1 Рис.6
В С
О
А Д
Тест 6. Угол между плоскостями.
Вариант 1.
Выберите верный ответ.
1. Плоскости  и
и 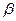 пересекаются по прямой с. Точка, лежащая в плоскости
пересекаются по прямой с. Точка, лежащая в плоскости  , удалена от плоскости
, удалена от плоскости 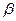 на
на  см, а от прямой с – на 4см. Угол между
см, а от прямой с – на 4см. Угол между  и
и 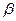 равен а) 300; б) 450; в) 600; г) 1350.
равен а) 300; б) 450; в) 600; г) 1350.
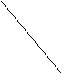
2. Прямая ДА перпендикулярна сторонам АВ и АС треугольника АВС и не лежит в его плоскости (рис. 1). Перпендикулярными являются плоскости а) ДАС и АВС; б) ДАВ и ДВС; в) ДАС и ДВС; г) ДВС и АВС.
 Д Рис. 1
Д Рис. 1
С А
В
3. Равнобедренные треугольники АВС и АДС имеют общее основание АС, причем ВД  АВС. ВМ – медиана треугольника АВС (рис. 2). Линейным углом для двугранного угла ДАСВ является угол
АВС. ВМ – медиана треугольника АВС (рис. 2). Линейным углом для двугранного угла ДАСВ является угол
а) ДАВ; б) ДСВ; в) ДМС; г) ДАС.
Д Рис.2

А В
М
С
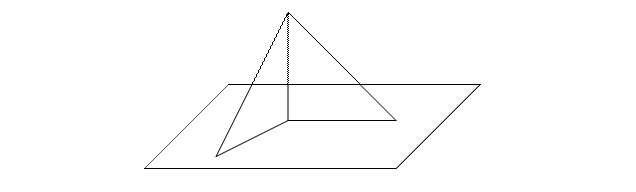
4. Пирамида ДАВС правильная. О – центр основания АВС, ОК – радиус окружности вписанной в основание (рис.3). Линейным для двугранного угла при основании является угол а) ДАО; б) ДСО; в) ДАС; г) ДКО.







 Д Рис. 3
Д Рис. 3
 А В
А В
 О
О
К
С
5. Через вершину А параллелограмма АВСД проведён к его плоскости перпендикуляр АМ (рис. 4). Линейным углом между плоскостями МАД и МАВ является угол а) МДА; б) ДАВ; в) МВА; г) МАД.
 М Рис. 4
М Рис. 4

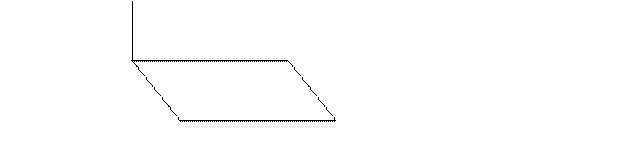
А В
Д С
6. АВСДА1В1С1Д1 прямоугольный параллелепипед в основании которого лежит квадрат АВСД. Боковая грань АА1В1В и диагональное сечение ВВ1 Д 1Д образуют угол равный а)) 300; б) 450; в) 600; г) 1350.
7. В треугольнике АВС  С = 900, МО // ВС. ДО – перпендикуляр к плоскости АВС (рис. 5). Линейным углом между плоскостями АВС и ДАС является угол а) ДАО; б) ДМО; в) ДСО; г) ДАС.
С = 900, МО // ВС. ДО – перпендикуляр к плоскости АВС (рис. 5). Линейным углом между плоскостями АВС и ДАС является угол а) ДАО; б) ДМО; в) ДСО; г) ДАС.
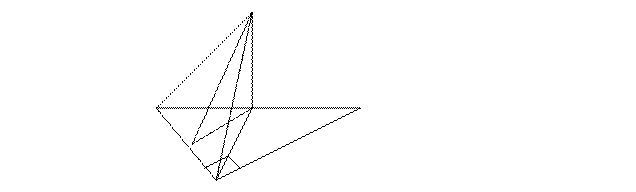 Д Рис.5
Д Рис.5
А О В
М
С
8. Катет АС прямоугольного треугольника АВС у которого  С = 900 лежит в плоскости
С = 900 лежит в плоскости  . ВД
. ВД  (рис.6). Линейным углом двугранного, образованного плоскостью
(рис.6). Линейным углом двугранного, образованного плоскостью  и плоскостью АВС, является угол
и плоскостью АВС, является угол
а) АСД; б) АСВ; в) АВД; г) АВС.


 В Рис. 6
В Рис. 6




С Д

А
9. АВСДА1В1С1Д1 - куб. Тангенс угла образованного основанием АВСД и плоскостью АВ1С (рис. 7) равен
|
|
|
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 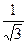 .
.
Рис. 7
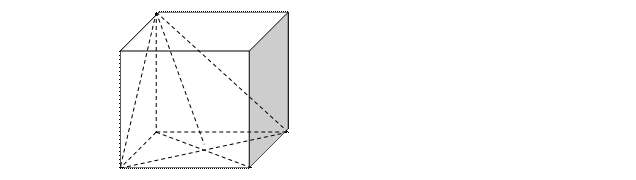 В 1 С1
В 1 С1
А1 Д1
В С
О
А Д
10. ДАВС – треугольная пирамида, АЕ  ДС и ВЕ
ДС и ВЕ  ДС (рис. 8). Линейным углом для двугранного ВДСА является угол
ДС (рис. 8). Линейным углом для двугранного ВДСА является угол
а) АДВ; б) АСВ; в) ЕАВ; г) АЕС.
 Д Рис. 8
Д Рис. 8
Е
А С
В
10. МАВС – пирамида, МА  АВС. Основание АВС – равнобедренный треугольник, АС = АВ. АК – медиана этого треугольника (рис. 9). Линейным углом для двугранного ВДСА является угол
АВС. Основание АВС – равнобедренный треугольник, АС = АВ. АК – медиана этого треугольника (рис. 9). Линейным углом для двугранного ВДСА является угол
а) МКА; б) КМА; в) МВА; г) МСА.
М Рис. 9

 |






А В
К
С
Тест 6. Угол между плоскостями.
Вариант 2.
Выберите верный ответ.
1.. Плоскости  и
и  пересекаются по прямой с. Точка, лежащая в плоскости
пересекаются по прямой с. Точка, лежащая в плоскости 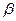 , удалена от плоскости
, удалена от плоскости  на 3 см, а от прямой с – на 6 см. Угол между
на 3 см, а от прямой с – на 6 см. Угол между  и
и 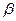 равен а) 300; б) 450; в) 600; г) 1500.
равен а) 300; б) 450; в) 600; г) 1500.
 2. Прямая МВ перпендикулярна сторонам АВ и ВС треугольника АВС и не лежит в его плоскости (рис. 1). Перпендикулярными являются плоскости а) МАС и АВС; б) МАВ и АВС; в) МАС и МВС; г) МВС и МАС.
2. Прямая МВ перпендикулярна сторонам АВ и ВС треугольника АВС и не лежит в его плоскости (рис. 1). Перпендикулярными являются плоскости а) МАС и АВС; б) МАВ и АВС; в) МАС и МВС; г) МВС и МАС.
М Рис.1
А В
С
3. Равнобедренные треугольники АВС и АВД имеют общее основание АВ, причем СД  АВС. СК – медиана треугольника АВС (рис. 2). Линейным углом для двугранного угла САВД является угол
АВС. СК – медиана треугольника АВС (рис. 2). Линейным углом для двугранного угла САВД является угол
а) ДАВ; б) ДВС; в) ДАС; г) СКД.
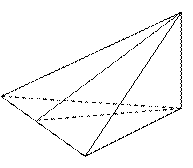 С
С
А Д
К
В
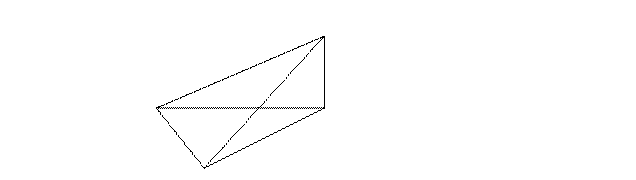
4. Пирамида КАВС правильная. О – центр основания АВС, ОН – радиус окружности вписанной в основание (рис.3). Линейным для двугранного угла при основании является угол а) КНО; б) КАО; в) КСО; г) НКО.
К Рис. 3
 |


 В А
В А
О
Н
С
5. Через вершину В треугольника АВС проведён к его плоскости перпендикуляр ВК (рис. 4). Линейным углом между плоскостями СКВ и АКВ является угол а) КСА; б) КАС; в) СВА; г) ВСА.
 К Рис. 4
К Рис. 4
С В
А
6. АВСДА1В1С1Д1 - куб. Боковая грань АА1В1В и диагональное сечение ВВ1 Д 1Д образуют угол равный а) 300; б) 450; в) 600; г) 1350.
6. АВСД – прямоугольная трапеция у которой  АВС = 900. ДК – перпендикуляр к плоскости трапеции (рис. 5). Линейным углом между плоскостью трапеции АВСД и плоскостью КАВ является угол
АВС = 900. ДК – перпендикуляр к плоскости трапеции (рис. 5). Линейным углом между плоскостью трапеции АВСД и плоскостью КАВ является угол
а) КАВ; б) КВД; в) КАД; г) АКД.
 К Рис. 5
К Рис. 5
Д
А
В С
8. Катет АВ прямоугольного треугольника АВС у которого  А = 900 лежит в плоскости
А = 900 лежит в плоскости  . СН
. СН  (рис.6). Линейным углом двугранного, образованного плоскостью
(рис.6). Линейным углом двугранного, образованного плоскостью  и плоскостью АВС, является угол
и плоскостью АВС, является угол
|
|
|


 а) САН; б) СВН; в) САВ; г) СВА.
а) САН; б) СВН; в) САВ; г) СВА.



 С Рис. 6
С Рис. 6
А Н
В 
9. АВСДА1В1С1Д1 - куб. Тангенс угла образованного основанием АВСД и плоскостью ВС1Д (рис. 7) равен
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 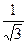 .
.
Рис. 7







 В1 С1
В1 С1
А1 Д1
В С
О
А Д
10. МАВС – треугольная пирамида, ВК  МА и СК
МА и СК  МА (рис. 8). Линейным углом для двугранного САМВ является угол
МА (рис. 8). Линейным углом для двугранного САМВ является угол
а) САВ; б) СКМ; в) ВКА; г) СКВ.

М Рис. 8
К
А В
С
11. КАВС – пирамида, КС  АВС. Основание АВС – равнобедренный треугольник, АС = ВС. СМ – медиана этого треугольника (рис. 9). Линейным углом для двугранного КАВС является угол
АВС. Основание АВС – равнобедренный треугольник, АС = ВС. СМ – медиана этого треугольника (рис. 9). Линейным углом для двугранного КАВС является угол
а) КАС; б) КМС; в) МКС; г) КВС.







 К Рис. 9
К Рис. 9
А С
М
В
|
|
|


