 |
Метод А. Ф. Смирнова для определения критических нагрузок в стержневых системах
|
|
|
|
1. ОСНОВНЫЕ ПРЕДПОСЫЛКИ
1)Нагрузка приложена только в узлах стержневой системы и до потери устойчивости не вызывает изгиба стержней.
2)Материал работает в упругой стадии.
3)Перемещения при потере устойчивости малы по сравнению с размерами конструкции
4)При определении перемещений учитываются продольные силы только в тех стержнях,в которых они возникали до потери устойчивости.
Примечание: Если критические нагрузки определяются в статически неопределимой системе, то ее статическая неопределимость раскрывается методом сил.
Основная система выбирается в момент потери устойчивости.
Основная система-это статически определимая и геометрически неизменяемая система, полученная из заданной путем удаления лишних связей в деформированном состоянии.
Основную систему рекомендуется выбирать таким образом, чтобы сжато-изогнутые элементы не имели смещений вдоль своих осей.
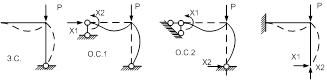
1.2.Алгоритм расчета по методу А.Ф.Смирнова
Рассмотрим упругую систему, загруженную узловыми нагрузками.
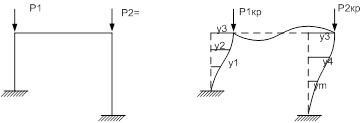
В момент потери устойчивости система характеризуется наличием сжато-изогнутых и изогнутых элементов.
Деформированное состояние системы характеризуется вектором отклонений Y, имеющим размер(m×1):
Y1
Y2
Y3
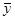 =...
=...
(m×1)...
Yn,
где m-число ненулевых координат вектора отклонений,которые задаются только для сжато-изогнутых стержней.
Вектор отклонений можно определить по формуле Мора,которая в матричной форме имеет вид
 (1.1)
(1.1)
При определении перемещений система разбивается на участки. В пределах каждого участка намечаются расчетные сечения по концам каждого участка и в тех точках сжато-изогнутых стержней, перемещение которых подлежит определению.
|
|
|
Обозначим: μ-число расчетных сечений
Для составления My необходимо в основной системе построить эпюры моментов от единичных сил приложенных в направлении искомых перемещений Y1,Y2,Y3...Yn.
Матрица Му имеет размер(μ×m)
Эпюра Эпюра Эпюра … Эпюра
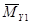

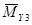
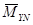
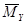 =
=
(μ×m)
G-размером (μ×μ)-матрица податливости всей системы.
Она формируется из матриц податливости отдельных участков.
Мр- матрица-столбец, элементами которой являются ординаты эпюр изгибающих моментов на тот период времени, когда заданная система находится в критическом состоянии.
Для статически-неопределимых систем при определении Мр используется матричный алгоритм метода сил:
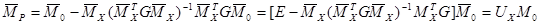
 (1.2),
(1.2),
где 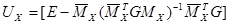 (1.3)-матрица,раскрывающая статическую неопределимость системы.
(1.3)-матрица,раскрывающая статическую неопределимость системы.
Если заданная система статически определимая,то матрица 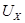 превращается в единичную матрицу (μ×μ):
превращается в единичную матрицу (μ×μ):
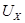 =Е (1.4)
=Е (1.4)
Структура матрицы 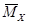
Эпюра Эпюра Эпюра … Эпюра

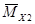
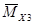

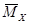 =
=
(μ×m)
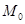 -матрица столбец, элементами которой являются ординаты эпюры моментов
-матрица столбец, элементами которой являются ординаты эпюры моментов 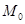 ,построенной от действия внешних узловых сил в основной системе,с учетом ее деформированного состояния.
,построенной от действия внешних узловых сил в основной системе,с учетом ее деформированного состояния.
Ординаты эп. 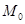 зависят от вектора перемещений y
зависят от вектора перемещений y
Получим матрицу 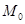 в виде:
в виде:
 (1.5),
(1.5),
где: H-числовая матрица размером (μ×m),преобразующая вектор отклонений у в эпюру моментов грузового состояния 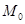
Тогда  (1.6)
(1.6)
Подставляя (1.6) в (1.1) получим вектор перемещений
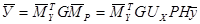 (1.7)
(1.7)
Обозначим: 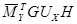 =k∙c (1.8),
=k∙c (1.8),
Где k-общий множитель,полученный из множителей при перемножаемым матрицах Н и G
Тогда:  или
или 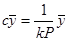 ,обозначим
,обозначим 
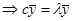 (1.9),
(1.9),
где:λ-собственное число матрицы 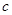 ;
; 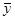 -собственный вектор матрицы
-собственный вектор матрицы 
Преобразуем (1.9)
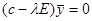 (1.10)-УРАВНЕНИЕ УСТОЙЧИВОСТИ МЕТОДА СМИРНОВА,
(1.10)-УРАВНЕНИЕ УСТОЙЧИВОСТИ МЕТОДА СМИРНОВА,
где  ;
;  .
.
Выражение (1.10) представляет собой систему однородных уравнений относительно 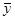 ,где матрица составлена из коэффициентов при неизвестных Y1,Y2,Y3...YN.
,где матрица составлена из коэффициентов при неизвестных Y1,Y2,Y3...YN.
|
|
|
Уравнение устойчивости (1.10) имеет два решения
1) Вектор перемещений 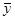 равен 0
равен 0
Y1 0
Y2 0
Y3 0
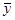 =... =... (1.11)-начальная форма равновесия
=... =... (1.11)-начальная форма равновесия
......
Yn 0
2) Определитель,составленный из коэффициентов при неизвестных 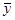 равен 0.
равен 0.
 =0 (1.12)-характеристическое уравнение
=0 (1.12)-характеристическое уравнение
Если раскрыть определитель,то получим уравнение m10 порядка,где неизвестным будет λ.
Решение этого уравнения дает значения λ,λ1,λ2,λ3…λm.
Минимальное значение Ркр составляет λmax (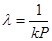 )
)
minPкр=  (1.13),
(1.13),
где 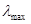 -наибольшее собственное число характеристической матрицы
-наибольшее собственное число характеристической матрицы 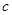 .
.
Собственный вектор характеристической матрицы 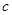 дает форму потери устойчивости.
дает форму потери устойчивости.
2. ПОРЯДОК РАСЧЕТА СИСТЕМ НА УСТОЙЧИВОСТЬ МЕТОДОМ А.Ф.СМИРНОВА
1.Заданная система изображается в критическом деформированном состоянии.
Выявляются сжато-изогнутые и изогнутые элементы, назначается число ненулевых координат вектора отклонений для сжато-изогнутых элементов.
2.Ось системы разбивается на участки.Назначаются расчетные сечения и правило знаков для эпюр изгибающих моментов.
3.Определяется степень статической неопределимости n и, если n>0 выбирается основная система метода сил.
4.Формируются необходимые матрицы 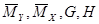 .
.
5.Вычисляется характеристическая матрица 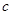
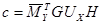 ,
,
где  -для статически неопределимых систем;
-для статически неопределимых систем;
 =Е-для статически определимых систем
=Е-для статически определимых систем
6.Решается характеристическое уравнение  =0 →
=0 → 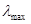
7.Определяется значение критической нагрузки:
minPкр= 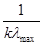
3. ФОРМИРОВАНИЕ МАТРИЦЫ ПОДАТЛИВОСТИ ДЛЯ СТЕРЖНЕВЫХ СИСТЕМ ПРИ РАСЧЕТЕ НА УСТОЙЧИВОСТЬ
Матрица податливости всей системы формируется из матриц податливости отдельных участков и имеет следующую структуру







 0
0
G= Gk
(μ×μ) Gk-матрица податливости участка k
Вид матрицы Gk зависит от типа участка (какую деформацию он испытывает).
1)Участок,испытывающий только изгиб
G 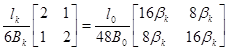 ,
,
где: l0-длина любого участка,принятого за основной
B0-жесткость любого участка,принятого за основную
|
|
|
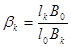 ;
;
2)Участки,испытывающие деформацию сжатие с изгибом. Для такого участка вид матрицы Gk зависит от того,на сколько панелей разбита его длина
а)Длина участка разбита на две панели:
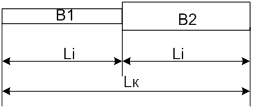
 -длина участка
-длина участка
 -длина панели
-длина панели
 ;
; 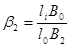

б)Длина участка разбита на три панели:

 ;
; 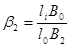 ;
; 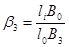
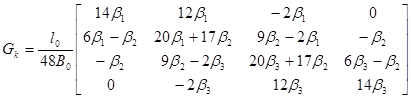
в)Длина участка разбита на четыре и более панелей:
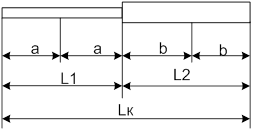
В этом случае общая длина сжато-изогнутого элемента компонуется из подучастков с двумя или тремя панелями. Соответственно и компонуется матрица податливости.
 | |||
 |









GΙ
 Gk = GΙ Ι
Gk = GΙ Ι
4. ФОРМИРОВАНИЕ МАТРИЦЫ H
Матрица H-числовая матрица размером (μ×m), преобразующая вектор перемещений 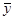 в эпюру моментов грузового состояния.
в эпюру моментов грузового состояния.
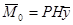 ;
;
Для построения матрицы H необходимо определить изгибающие моменты во всех расчетных сечениях основной системы от узловых нагрузок и построить эпюру М0

Эпюра М0 строится со стороны растянутых волокон с учетом деформированного состояния системы.



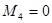
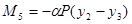


М0= 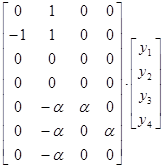
В матрицу H вписываются коэффициенты при перемещениях из каждого уравнения.
5. РЕШЕНИЕ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ
Существует несколько методов решения характеристического уравнения. Все методы делятся на две группы:
1)Первая –позволяет вычислить все собственные числа(метод Крылова-Лузина и др.)
2)Вторая –позволяет вычислить наибольшее собственное число(и соответственно наименьшее значение критической нагрузки)
К этой группе относится метод последовательных приближений
Метод итераций позволяет вычислить наибольшее собственное число характеристической матрицы  .Вместе с определением собственного числа одновременно производится определение собственного вектора, соответствующего этому числу и удовлетворяющего равенству:
.Вместе с определением собственного числа одновременно производится определение собственного вектора, соответствующего этому числу и удовлетворяющего равенству:
 ,
,
где 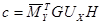 -характеристическая матрица
-характеристическая матрица
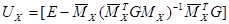 -для статически неопределимых систем
-для статически неопределимых систем
 =Е- для статически определимых
=Е- для статически определимых
|
|
|
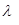 - собственное число характеристической матрицы
- собственное число характеристической матрицы 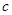
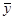 -собственный вектор матрицы
-собственный вектор матрицы 
Порядок решения:
1)Задаемся приближенным вектором перемещений 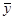 -первое приближение;
-первое приближение;
2)Вычисляется: 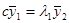 ,
,
где  -второе приближение собственного вектора;
-второе приближение собственного вектора; 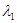 -первое приближение собственного числа.
-первое приближение собственного числа.
Вектор 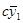 следует сделать нормированным,т.е. его наибольшую координату надо вынести за знак матрицы в виде множителя
следует сделать нормированным,т.е. его наибольшую координату надо вынести за знак матрицы в виде множителя 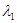 .
.
3)Далее вновь подсчитывается:
 и т.д.
и т.д.
4)Повторение процесса продолжается до тех пор,пока значения координат векторов двух последних приближений не совпадут.
Величина 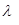 найденная в последнем приближении принимается за искомое
найденная в последнем приближении принимается за искомое 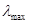
6. ПРИМЕР.
Определить критическую силу методом А.Ф.Смирнова
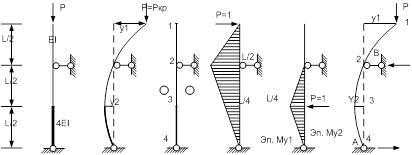
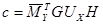 ;
;  =Е- т.к. система статически определима
=Е- т.к. система статически определима
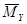 =
=  ;
;  ;
; 
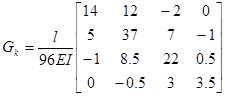 ;
;
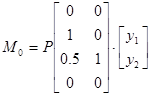 ;
;
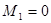
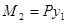
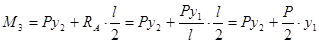

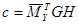
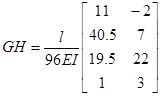 ;
; 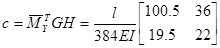
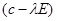 =0
=0
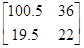 =0
=0


| С | С= 
| 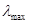
|
| у1 | 1 | 0,5 | |
| Су1 | 118,5 | 30,5 | 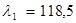
|
| у2 | 1 | 0,257 | |
| Су2 | 109,75 | 25,15 | 
|
| у3 | 1 | 0,229 | |
| Су3 | 108,74 | 24,54 | 
|
| у4 | 1 | 0,2257 | |
| Су4 | 108,62 | 24,46 | 
|
| у5 | 1 | 0,225 |
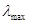 =108,62
=108,62
у= 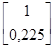

minPкр= 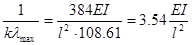 ;
;
|
|
|


