 |
Краткие теоретические сведения. Рекурсия – это второе средство для организации повторяющихся действий в Prologе
|
|
|
|
Рекурсия – это второе средство для организации повторяющихся действий в Prologе. Рекурсивная процедура – это процедура, вызывающая сама себя до тех пор, пока не будет соблюдено некоторое условие, которое остановит рекурсию. Такое условие называют граничным. Рекурсия – хороший способ для решения задач, содержащих в себе подзадачу такого же типа. Правило является рекурсивным, если оно принадлежит процедуре, включающей вызов самой себя в виде подцели, содержащейся в теле по крайней мере одного из ее утверждений.
В общем случае рекурсивное правило имеет следующий вид:
recursive_rule(<фактические параметры через запятую>): -<предикаты и правила>,recursive_rule(<фактические параметры рекурсивного вызова>).
Классическим примером рекурсивного определения в Прологе может служить процедура «предок», которая состоит из двух правил:
предок(Х,Y):-родитель(X,Y).
предок(Х,Y):-родитель(Z,Y), предок(X,Y).
Совокупность этих правил определяет два способа, в соответствии с которыми одно лицо (Х) может быть предком другого лица (Y). Согласно первому правилу, Х является предком Y, если Х – родитель Y, т.е. Х является ближайшим предком Y.
Согласно второму правилу. Х будет предком Y, если есть некоторый Z, который, являясь родителем Y, имеет своим предком Х. Другими словами, Х – предок Y, если Х – предок родителя Y, т.е. Х – отдаленным предком Y. Таким образом второе правило зависит от более простой версии самого себя, т.е. от подцели «предок».
Примером рекурсивных вычислений является известный алгоритм вычисления факториала. Hа Прологе эта программа может иметь такой вид:
Domains
N,F=real
Predicates
factorial(N,F)
Clauses
factorial(1,1).
factorial(N,R):- N>0, N1=N-1,
factorial(N1,R1), R=R1*N.
Goal
factorial(8,F),write(F).
|
|
|
При каждом вызове дизъюнкта factorial генерируются новые переменные, которые действуют всегда только на своем уровне вложенности, пока не встретится условие прекращения вычислений. Только после этого на обратном пути прохождения рекурсии определяются результаты, которые передаются вверх.
Вообще, любая рекурсивная процедура должна содержать хотя бы одну из двух компонент:
1. Нерекурсивную фразу, определяющую правило, применяемое в момент прекращения рекурсии.
2. Рекурсивное правило, первая подцель которого вырабатывает новые значения аргументов, а вторая – рекурсивная подцель – использует эти значения.
База правил просматривается сверху вниз. Сначала делается попытка выполнения нерекурсивной фразы. Если условие окончания рекурсии не указано, то правило может работать бесконечно.
Любое рекурсивное определение содержит по крайней мере одно нерекурсивное правило и одно или несколько правил с рекурсией. В большинстве случаев имеется по одному правилу каждого типа. Считается, что используется хвостовая рекурсия, если последнее условие в последнем правиле является рекурсивным. Такая рекурсия имеет преимущество перед нехвостовой рекурсией, так как позволяет ограничить рост стека и строго контролировать процесс возврата. Это происходит благодаря очистке стека после успешного сопоставления условия, содержащего рекурсию.
Начинающему пользователю бывает довольно трудно понять, каким образом выполняется рекурсивная процедура, будучи вызванной в качестве цели. Поэтому в последующем разделе на примере работы со списками будет продемонстрировано выполнение некоторых рекурсивных процедур.
Пример решения задачи «Ханойская башня» на ПРОЛОГе.
DOMAINS
loc =right;middle;left
PREDICATES
hanoi(integer)
move(integer,loc,loc,loc)
inform(loc,loc)
GOAL
hanoi(5).
CLAUSES
hanoi(N):- move(N,left,middle,right).
move(1,A,_,C):- inform(A,C),!.
move(N,A,B,C):- N1=N-1, move(N1,A,C,B), inform(A,C),
move(N1,B,A,C).
|
|
|
inform(Loc1, Loc2):- nl,write(“Диск с”, Loc1, “ на “, Loc2).
Варианты заданий
Вариант 1. Подсчитать, сколько раз встречается некоторая буква в строке. Строка и буква должны вводиться с клавиатуры. Для разделения строки на символы использовать стандартный предикат frontchar (String, Char, StringRest), позволяющий разделять строку String на первый символ Char и остаток строки StringRest.
Вариант 2. Вычислить значение n-го члена ряда Фибоначчи: f(0)=0, f(1)=1, f(n)=f(n-1)+f(n-2).
Вариант 3. Вычислить произведение двух целых положительных чисел (используя суммирование).
Вариант 4. Подсчитать, сколько раз встречается некоторое слово в строке. Строка и слово должны вводиться с клавиатуры. Для разделения строки на слова использовать стандартный предикат fronttoken (String, Lexeme, StringRest), позволяющий разделить строку String на первое слово Lexeme и остаток строки StringRest.
Вариант 5. Поменять порядок следования букв в слове на противоположный. Для разделения строки на символы использовать стандартный предикат frontchar (String, Char, StringRest), позволяющий разделять строку String на первый символ Char и остаток строки StringRest.
Вариант 6. Вычислить сумму ряда целых нечетных чисел от 1 до n.
Вариант 7. Поменять порядок следования слов в предложении на противоположный. Для разделения строки на слова использовать стандартный предикат fronttoken (String, Lexeme, StringRest), позволяющий разделить строку String на первое слово Lexeme и остаток строки StringRest..
Вариант 8. Вычислить сумму ряда целых четных чисел от 2 до n.
Вариант 9. Организовать ввод целых положительных чисел и их суммирование до тех пор, пока сумма не превысит некоторого порогового значения. Введенные отрицательные целые числа суммироваться не должны.
Вариант 10. Организовать ввод букв и их соединение в строку до тех пор, не будет введен символ #. Для присоединения символа к строке использовать стандартный предикат frontchar (String, Char, StringRest), позволяющий присоединять символ Char к строке StringRest и получать строку String.
Вариант 11. Написать рекурсивную программу вычисления п-го члена геометрической прогрессии, суммы ее п первых членов и суммы ее членов, начиная с i -го по к-й.
Вариант 12. Описать рекурсивную функцию вычисления максимального числа Фибоначчи, ближайшего к заданному п по недостатку.
Вариант 13. Написать подпрограмму-функцию степени аx, где a, х – любые числа. Воспользуемся формулой: аx = ex ln a
|
|
|
Вариант 14. Используя рекурсию составить программу вычисления суммы. Значения k и n ввести с клавиатуры.  .
.
Вариант 15. Написать программу вычисления суммы n первых членов бесконечного ряда 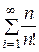 .
.
Вариант 16. Написать программу для вычисления чисел Фибоначчи для ряда, заданного списком.
Вариант 17. Написать программу для вычисления среднего арифметического списка чисел.
Вариант 18. Написать программу для генерации ряда целых чисел от M до N в порядке возрастания.
Вариант 19. Написать программу для генерации ряда целых чисел от M до N в порядке убывания.
Вариант 20. Написать программу, которая бы воспринимала целые числа с клавиатуры и вычисляла сумму введенных десятичных чисел. Программа должна завершаться при вводе числа 0.
Отчет по лабораторной работе должен содержать: титульный лист с указанием номера варианта; текст задания; исходные тексты программы с комментариями.
Контрольные вопросы:
1. Что такое рекурсия? Привести примеры.
2. Дать рекурсивную формулировку понятиям «предок» и «потомок».
3. Дать определение следующего понятия: рекурсия, базис рекурсии, шаг рекурсии.
4. Назначение предиката fail.
5. рганизация рекурсивных вычислений в Прологе.
Лабораторная работа № 3
|
|
|


