 |
Кривые в природе и жизни человека
|
|
|
|
Департамент образования Вологодской области
Бюджетное профессиональное образовательное учреждение Вологодской области
«Вологодский строительный колледж»
Номинация: Лучший проект по математическим дисциплинам
Проект по дисциплине: Математика.
Тема: «Замечательные кривые: спирали и розы».
| Выполнили: Баринова Екатерина Сергеевна Давыдова Алена Руслановна Группа: 153 Отделение: Земельно-имущественные отношения Проверил: Преподаватель: Севалёва Елена Анатольевна |
Вологда 2017
СОДЕРЖАНИЕ
3. Спирали и розы Вологодчины………………………………………….…13
3.1. Кружевоплетение……………………………………………………….…13
3.2. Северная чернь………………………………………………………….…13
3.3. Устюжская финифть………………………………………………………14
3.4. Роспись по дереву………………………………………………………….14
4. Социологический опрос………………………………………………..16 – 17
5. Заключение……………………………………………………………………18
6. Литература…………………………………………………………………….19 | |||||||||||||||||||||||||||||||||
ВВЕДЕНИЕ
В школьном курсе математики рассматриваются кривые – Эллипс, Кардиоида и Улитка Паскаля, Циклоида, Спираль Архимеда, Парабола.
Но нигде не говорится о замечательных свойствах данных кривых, а тем более об их практическом применении. Считается, что очень важно учащимся знать замечательные свойства данных кривых, которые широко применяются в жизни. Исследуя и даже просто знакомясь с этими свойствами, учащиеся видят действительно практическое применение математики.
Актуальность: Эту тему мы выбрали потому, что хотела поближе познакомиться с замечательными кривыми. Узнать, используются ли в архитектуре нашего города, т.е. города Вологды эти элементы математики.
Гипотеза: Замечательные кривые существуют в жизни человека.
Объект: Замечательные кривые.
Предмет исследования: Математика.
Цель проекта: Познакомиться с некоторыми замечательными кривыми, которые встречаются и имеют практическое применение в нашей жизни.
Задачи работы:
1 Изучить источники на бумажных носителях и в Интернете.
2 Провести анализ найденных материалов.
3. Ознакомление с практическим применением кривых в жизни человека.
4 Написание проекта.
5.Презентация проекта.
СПИРАЛИ И РОЗЫ
1.1Открытие спирали 
Архимедова спираль была открыта Архимедом. Это произошло в III веке до н.э., когда он экспериментировал с компасом. Он тянул стрелку компаса с постоянной скоростью, вращая сам компас по часовой стрелке. Получившаяся кривая была спиралью, которая сдвигались на ту же величину, на которую поворачивался компас, и между витками спирали сохранялось одно и то же расстояние.
Согласно Математической Энциклопедии, спиралями называются плоские кривые, которые "обычно обходят вокруг одной (или нескольких точек), приближаясь или удаляясь от нее”. Это толкование термина не является строго формализуемым определением. Если какая-то известная кривая содержит в названии эпитет "спираль", то к этому следует относиться как к исторически сложившемуся названию.
|
|
|
Виды спиралей
Спираль Архимеда.
Безобидная воронка, образованной вытекающей из ванны водой; свирепый смерч, опустошающий все на своем пути; величественный круговорот гигантского космического вихря туманностей и галактик – все они имеют форму спиралей. Одну из первых спиралей, описанную Архимедом, нам продемонстрирует светлячок. Отправим его в путешествие вдоль секундной стрелки часов, полагая, что он будет перемещаться с постоянной скоростью, не обращая внимания на равномерное движение стрелки часов по кругу. Если вообразить бесконечно, длинную стрелку, то жучок высветит нам «спираль Архимеда» (в переводе с латыни спираль означает «изгиб», «извив»). Геометрическим свойством, характеризующим спираль Архимеда, является постоянство расстояний между витками
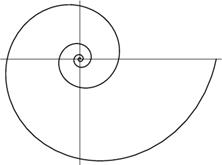
Рис. 2 Архимедова спираль
Архимедова спираль – плоская кривая, описываемая точкой M, равномерно движущейся по прямой OA, в то время как эта прямая равномерно вращается в плоскости вокруг одной из своих точек O. Спираль Архимеда состоит из бесконечно многих витков. Она начинается в центре, и все более и более удаляется от него по мере того, как растет число оборотов. На рисунке изображены первый виток и часть второго
Рис 3. Построение Архимедовой спирали.
Спираль Ферма
Параболическая спираль — спираль, задаваемая на плоскости в полярных координатах уравнением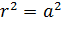 
φ{displaystyle r^{2}=a^{2}varphi }. Является видом Архимедовой спирали.
Гиперболическая спираль.
Гиперболическая спираль - плоская трансцендентная кривая. Уравнение гиперболической спирали в полярной системе координат является обратным для уравнения Архимедовой спирали и записывается так:
ρφ=α
Рис. 5 Гиперболическая спираль.
Логарифмическая спираль.
Слово логарифм происходит от греческого (число, отношение), и переводится как отношение чисел. Джон Непер (1550-1617гг.) шотландский математик, изобретатель логарифмов объяснял, что логарифмы возникли при сопоставлении двух чисел, одно из которых является членом арифметической прогрессии, а другое геометрической. Логарифмы с основанием ввѐл Спейдел. Логарифмы необычайно быстро вошли в практику.
|
|
|
Рис. 6 Логарифмическая спираль.
Логарифмическая спираль – это линии в геометрии, отличные от прямых и окружностей, которые могут скользить по себе. Логарифмическую спираль называют равноугольной спиралью. Это ее название отражает тот факт, что в любой точке логарифмической спирали угол между касательной к ней и радиус – вектором сохраняет постоянное значение.
Клотоида или Спираль Корню.
(в западной литературе известна так же как спираль Эйлера) — кривая, у которой кривизна изменяется линейно как функция длины дуги.
1/R~L↔R*L=const
Рис. 7 Клотоида или Спираль Корню.
Сферическая спираль.
Сферическая спираль (локсодрома) — это кривая на сфере, пересекающая все меридианы под одним углом (не прямым). Эта кривая имеет бесконечное число витков. Расстояние между ними убывает по мере приближения к полюсам.
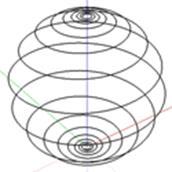
Рис. 8 Сферическая спираль.
Роза
Роза— плоская кривая, напоминающее символическое изображение цветка.
История открытия
Впервые об этой кривой упоминает флорентийский монах Гвидо Гранди в двух письмах Лейбницу в декабре 1713 года и называет её «розовидной». Через десять лет он опубликовал статью о ней в «Философских трудах Королевского общества», где рассмотрел разновидности этой кривой с различным количеством лепестков и также называл их «розовидными». Ещё через пять лет Гвидо Гранди развил теорию розовидных кривых в отдельном труде, где наряду с этим рассмотрел похожие на них пространственные кривые, лежащие на сфере, которые он назвал «клелиями» в честь княгини Клелии Борромео.
Полярная роза
Полярная роза- это плоская кривая, напоминающее символическое изображение цветка.
Рис. 10 Полярная роза
Семейство роз Гранди описывается уравнением в полярных координатах г=a sinк, где а и к - некоторые постоянные. При к нечётном роза состоит из к лепестков, при m чётном — из 2к лепестков; при к рациональном лепестки частично покрывают друг друга. При иррациональном K роза имеет бесконечное число лепестков. В уравнении r=asin(bk) значение a отвечает за длину лепестков, а значения b – за количество и форму.
|
|
|
Рис. 11 Общий вид полярной розы, задаваемой уравнением при различных значениях К.
Декартов лист
Декартов лист - плоская алгебраическая кривая третьего порядка, удовлетворяющая уравнению в прямоугольной системе x3 + y3 = 3xy
Рис. 12 Декартов лист.
Впервые уравнение кривой исследовал Р. Декарт в 1638 году, однако он построил только петлю в первом координатном угле, где {displaystyle x}x и {displaystyle y}y принимают положительные значения. Декарт полагал, что петля симметрично повторяется во всех четырёх координатных четвертях, в виде четырёх лепестков цветка. В то время эта кривая называлась цветком жасмина (англ. jasmine flower, фр. fleur de jasmin). В современном виде эту кривую впервые представил Х. Гюйгенс в 1692 году.
КРИВЫЕ В ПРИРОДЕ И ЖИЗНИ ЧЕЛОВЕКА
Спирали в природе
Поражает необычайное разнообразие значений символа спирали. Он воспринимается как ход и бег времени (циклические ритмы, смена солнечных и лунных фаз, ход истории, человеческой жизни). Спираль считается знаком развития, жизненной силы, данной нам природой. Это стремление к новым уровням, к своему центру, мудрости. Спираль часто ассоциируется со змеей, олицетворяющей, в свою очередь, мудрость предков. Ведь известно, что змеи очень любят сворачиваться кольцами и внешне походят на спирали. В природе спираль проявляется в трех основных формах: застывшей (раковины улитки), расширяющейся (изображения спиральных галактик) или сжимающейся (подобие водоворота). Спиральные формы представлены от эволюционных глубин (молекулы ДНК) до законов диалектики. Спираль близка к кругу - самой идеальной форме из всех, что создала природа. Действительно, стихийные и природные элементы, имеющие форму спирали, очень распространены в природе. Это спиральные туманности, галактики, водовороты, смерчи, торнадо, устройства растений. Даже пауки спиралеобразно плетут паутину, закручивая нити по спирали вокруг центра. Природа любит повторения, в ее творениях использованы одни и те же принципы.
Рис 13. Природные элементы, имеющие форму спирали.
Рога некоторых рогатых животных закручены по спирали Архимеда, например у вилорога и болотного козла. А бутоны розы тоже напоминают спираль. Также спираль Архимеда используют в винтах самолетов и кораблей. Даже вселенная имеет вид спирали Архимеда.
Рис 14. Раковина моллюска, хорошо напоминает нам спираль.
|
|
|
На этой сосновой шишке можно рассмотреть двойную спираль, одна движется в одном, а другая в другом направлении.
Рис 14. Двойная спираль
В подсолнухе мы можем рассмотреть, как растут семена похожие на спирали.
Рис 15. Подсолнух.
Так же спирали можно разглядеть на кончиках пальцев.
Рис 16. Папиллярные узоры.
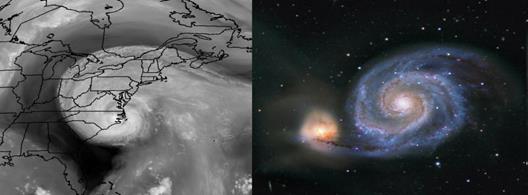Вид из космоса - «спираль Архимеда».
Спирали в технике
Применение в технике Спираль Архимеда в настоящее время широко используется в технике. Одно из изобретений ученого - винт (прообраз объемной спирали) - использовалось как механизм для передачи воды в оросительные каналы из низколежащих водоемов. Винт Архимеда стал прообразом шнека («улитки») - устройства, широко используемого в различных машинах для перемешивания жидких, сыпучих и тестообразных материалов. Самая распространенная его разновидность - винтовой ротор в обычной мясорубке.
Рис 17. Мясорубка.
Примером применения в технике архимедовой спирали также является самоцентрирующийся патрон. Данный механизм используется в швейных машинках для равномерного наматывания ниток. Ныне спираль Архимеда заслуживает особого внимания при обучении компьютерной графике
Применение роз Гранди
Розы Гранди нашли свое применение в технике, в частности, если некоторая точка совершает колебание вдоль прямой, вращающейся с постоянной этой точки будет розой.
|
3.
|
|
|
