 |
Свойства бинарных отношений
|
|
|
|
Аксиомы ZFC
1. Аксиома объёмности. Два множества a и b равны тогда и только тогда, когда они имеют одни и те же элементы.
∀ a ∀ b (a = b ↔∀ c (c ∈ a ↔ c ∈ b))
2. Аксиома пустого множества. Существует множество e без единого элемента. Это множество обычно обозначается {} или ∅.
∃ e ∀ a (a ∉ e)
3. Аксиома пары [1]. Для любых множеств a и b существует множество c такое, что a и b являются его единственными элементами. Множество c обозначается { a, b } и называется неупорядоченной парой a и b. Если a = b, то c состоит из одного элемента.
∀ a ∀ b ∃ c ∀ d (d ∈ c ↔(d = a ∨ d = b))
4. Аксиома объединения. Для любого семейства a множеств существует множество b =∪ a, называемое объединением множества a, состоящее из тех и только тех элементов, которые содержатся в элементах множества a.
∀ a ∃ b ∀ c (c ∈ b ↔∃ d (d ∈ a ∧ c ∈ d))
5. Аксиома бесконечности. Аксиомы с 1 по 4 предоставляют ограниченные возможности для формирования новых множеств. Так, по теореме Кантора во множестве P(a) имеется элемент, не принадлежащий a, поэтому, например, не существует «множества всех множеств» (парадокс Рассела). Далее введём определение: множество называется индуктивным, если оно а) содержит пустое множество и б) содержит последователь (то есть элемент a ∪{ a }) каждого своего элемента. Аксиома бесконечности утверждает, что индуктивные множества существуют.
∃ ω (∅∈ ω ∧∀ x (x ∈ ω → x ∪{ x }∈ ω))
6. Схема выделения. Любому множеству a и свойству φ отвечает множество b, элементами которого являются те и только те элементы a, которые обладают свойством φ. Схема выделения содержит счётное количество аксиом, так как каждая формула φ (x) логики первого порядка порождает аксиому.
|
|
|
∀ a ∃ b ∀ c (c ∈ b ↔(c ∈ a ∧ φ (c)))
7. Аксиома множества подмножеств. Для любого множества a существует множество b, состоящее из тех и только тех элементов, которые являются подмножествами множества a. Множество подмножеств множества a обозначается P(a).
∀ a ∃ b ∀ c (c ∈ b ↔∀ d (d ∈ c → d ∈ a))
Если ввести отношение подмножества ⊆, то эту формулу можно упростить.
∀ a ∃ b ∀ c (c ∈ b ↔ c ⊆ a)
8. Схема подстановки. Пусть φ (x, y) — такая формула, что при некоторых x 0 из множества X существует, и притом единственный, объект y 0 такой, что выражение φ (x 0, y 0) истинно. Тогда объекты c, для каждого из которых существует d из X такой, что φ (d, c) истинно, образуют множество. Схема подстановки содержит счётное количество аксиом, так как каждая подходящая формула φ (x, y) порождает аксиому.
∀ x ∃! y (φ (x, y))→∀ a ∃ b ∀ c (c ∈ b ↔(∃ d (d ∈ a ∧ φ (d, c)))
9. Аксиома основания. Каждое непустое множество s содержит элемент a такой, что s ∩ a =∅.
∀ s (s ≠∅→∃ a (a ∈ s ∧ a ∩ s =∅))
10. Аксиома выбора. Для любого семейства попарно непересекающихся непустых множеств существует множество c такое, что, каково бы ни было множество x данного семейства, множество x ∩ c состоит из одного элемента.
2. Отношения.
2.1. Способы установления отношений. 


2.2. Однородные бинарные отношения.
Пусть  и
и  два конечных множества. Декартовым произведением множеств
два конечных множества. Декартовым произведением множеств  и
и  называют множесто
называют множесто  состоящее из всех упорядоченных пар, где
состоящее из всех упорядоченных пар, где 
Бинарным отношением между элементами множества  и
и  называется любое подмножество
называется любое подмножество  множества
множества  , то есть
, то есть 
По определению, бинарным отношением называется множество пар. Если R — бинарное отношение (т.е. множество пар), то говорят, что параметры  и
и  связаны бинарным отношением
связаны бинарным отношением  , если пара
, если пара  является элементом R, т.е.
является элементом R, т.е. 
|
|
|
Высказывание: «предметы  и
и  связаны бинарным отношением
связаны бинарным отношением  » записывают в виде
» записывают в виде  Таким образом,
Таким образом, 
Если  , то говорят, что бинарное отношение определено на множестве
, то говорят, что бинарное отношение определено на множестве  .
.
Примеры бинарных отношений:
· на множестве целых чисел  отношения «делится», «делит», «равно», «больше», «меньше», «взаимно просты»;
отношения «делится», «делит», «равно», «больше», «меньше», «взаимно просты»;
· на множестве прямых пространства отношения «параллельны», «взаимно перпендикулярны», «скрещиваются», «пересекаются», «совпадают»;
· на множестве окружностей плоскости «пересекаются», «касаются», «концентричны».
Областью определения бинарного отношения  называется множество, состоящее из таких
называется множество, состоящее из таких  , для которых
, для которых  хотя бы для одного
хотя бы для одного  .
.
Область определения бинарного отношения будем обозначать 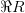 .
.

Областью значений бинарного отношения  называется множество, состоящее из таких
называется множество, состоящее из таких  , для которых
, для которых  хотя бы для одного
хотя бы для одного  .
.
Область значений бинарного отношения будем обозначать 

Инверсия (обратное отношение)  — это множество
— это множество 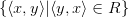 и обозначается, как
и обозначается, как 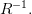
Композиция (суперпозиция) бинарных отношений  и
и  — это множество
— это множество  и обозначается, как
и обозначается, как  .
.
2.3. Рефлексивность, симметрия, антисимметрия и транзитивность однородных бинарных отношений.
Свойства бинарных отношений
Бинарное отношение  на некотором множестве
на некотором множестве  может обладать различными свойствами, например:
может обладать различными свойствами, например:
o Рефлексивность: 
o Антирефлексивность (иррефлексивность): 
o Корефлексивность: 
o Симметричность: 
o Антисимметричность: 
o Асимметричность:  . Асимметричность эквивалентна одновременной антирефлексивности и антисимметричности отношения.
. Асимметричность эквивалентна одновременной антирефлексивности и антисимметричности отношения.
o Транзитивность: 
o Связность: 
Виды отношений
o Рефлексивное транзитивное отношение называется отношением квазипорядка
o Рефлексивное симметричное транзитивное отношение называется отношением эквивалентности
o Рефлексивное антисимметричное транзитивное отношение называется отношением (частичного) порядка
o Антирефлексивное антисимметричное транзитивное отношение называется отношением строгого порядка
o Полное антисимметричное (для любых  выполняется
выполняется  или
или  ) транзитивное отношение называется отношением линейного порядка
) транзитивное отношение называется отношением линейного порядка


3. Отношение эквивалентности.
3.1. Эквивалентности, классы эквивалентности, фактор-множество. 

4. Сила множеств.
4.1. Мощность множеств, сравнение мощностей, мощность конечных множеств.
|
|
|

Мощность (кардинальное число) множества - такое свойство множества, которое остается после абстрагирования от качества (состава) его элементов (определение мощности по Кантору). Мощность множества А обозначается | А | или gard A. 






4.2. Примеры и свойства счетных множеств.




4.3. Теорема Кантора - Бернштейна.


4.4. Несчетность множества вещественных чисел интервала (0; 1).


4.5. Примеры и свойства континуальных множеств.
Континуальное множество - любое бесконечное множество, равномощное множеству R действительных чисел. Говорят, что всякое континуальное множество имеет мощность континуума. Такой мощностью обладают, например:
множество всех подмножеств всякого счетного множества;
множество точек, принадлежащих некоторой прямой или поверхности;
множество всех действительных чисел некоторого интервала (a,b) или отрезка [ a,b ]
В отличие от счетного множества, элементы континуального множества не могут быть пронумерованы, т.е. множество-континуум несчетно. Справедливость данного утверждения подтверждается теоремой Кантора.

4.6. Мощность множества всех подмножеств. Шкала мощностей. Гипотеза континуума.


5. Отношения частичного порядка.
5.1. Частичный порядок, диаграммы чум.

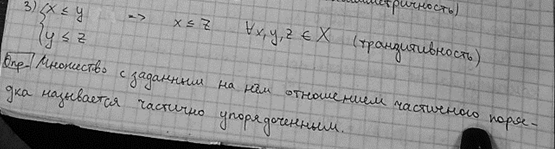



5.2. Верхний и Нижний конусы, максимальный и минимальный элементы, максимум,
минимум, точные верхние и нижние грани в ЧУМ.


5.3. Вполне упорядоченные множества



5.4. Аксиома выбора, теорема Цермело и эквивалентные утверждения.

5.5. Построение множества действительных чисел Дедекиндом (основные этапы).







6. Универсальная алгебра.
6.1. Алгебры и подалгебры, их гомоморфизмы и изоморфизмы. 


7. Решетки.
7.1. Решетки как кеты и как алгебры. Эквивалентность двух определений.




7.2. Дистрибутивная решетка. Критерий дистрибутивности.


7.3. Решетка с дополнениями.

8. Булева алгебра.
8.1. Булева алгебра. Примеры булевых алгебр и булевых решеток.


8.2. Теорема Стоуна о конечных булевых алгебрах.
|
|
|

8.3. Примеры бесконечных булевых алгебр
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
9. Отношение сравнимости по модулю m.
9.1. Свойства сравнений по модулю.








9.2. Число решений линейного сравнения с 1 неизвестным, условия его разрешимости.


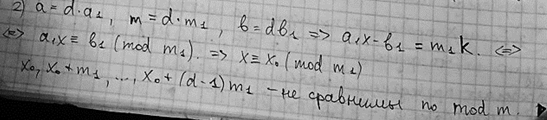
9.3. Малая теорема Ферма.

9.4. Китайская теорема об остатках.

9.5. Функция Эйлера. Теорема Эйлера.
Функция Эйлера  (иногда обозначаемая
(иногда обозначаемая  или
или  ) — это количество чисел от
) — это количество чисел от  до
до 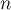 , взаимно простых с
, взаимно простых с 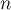 . Иными словами, это количество таких чисел в отрезке
. Иными словами, это количество таких чисел в отрезке  , наибольший общий делитель которых с
, наибольший общий делитель которых с 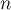 равен единице.
равен единице.
Несколько первых значений этой функции (A000010 в энциклопедии OEIS):



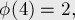

Свойства
Три следующих простых свойства функции Эйлера — достаточны, чтобы научиться вычислять её для любых чисел:
· Если  — простое число, то
— простое число, то  .
.
(Это очевидно, т.к. любое число, кроме самого  , взаимно просто с ним.)
, взаимно просто с ним.)
· Если  — простое,
— простое,  — натуральное число, то
— натуральное число, то  .
.
(Поскольку с числом  не взаимно просты только числа вида
не взаимно просты только числа вида 
 , которых
, которых  штук.)
штук.)
· Если  и
и  взаимно простые, то
взаимно простые, то  ("мультипликативность" функции Эйлера).
("мультипликативность" функции Эйлера).
(Этот факт следует из китайской теоремы об остатках. Рассмотрим произвольное число  . Обозначим через
. Обозначим через  и
и  остатки от деления
остатки от деления  на
на  и
и  соответственно. Тогда
соответственно. Тогда  взаимно просто с
взаимно просто с  тогда и только тогда, когда
тогда и только тогда, когда  взаимно просто с
взаимно просто с  и с
и с  по отдельности, или, что то же самое,
по отдельности, или, что то же самое,  взаимно просто с
взаимно просто с  и
и  взаимно просто с
взаимно просто с  . Применяя китайскую теорему об остатках, получаем, что любой паре чисел
. Применяя китайскую теорему об остатках, получаем, что любой паре чисел  и
и 
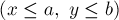 взаимно однозначно соответствует число
взаимно однозначно соответствует число 
 , что и завершает доказательство.)
, что и завершает доказательство.)
Отсюда можно получить функцию Эйлера для любого  через его факторизацию (разложение
через его факторизацию (разложение 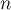 на простые сомножители):
на простые сомножители):
если

(где все  — простые), то
— простые), то


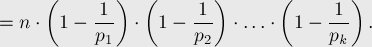

9.6. Теорема Вильсона.


9.7. Квадратичные вычеты и невычеты.






10. Линейные диофантовы уравнения.
10. 1. Решение линейных диофантовых уравнений с n неизвестными.


11. Группы.
11. 1. Группы. Определение, примеры и простейшие свойства.




11. 2. Подгруппы. Циклические подгруппы. Порядок элементов.


11. 3. Смежные классы элементов по подгруппе, теорема Лагранжа.


11. 4. Гомоморфизмы и изоморфизмы групп.



11. 5. Нормальные подгруппы.


12. Кольца и поля.
12. 1. Кольца. Делители нуля.
Определение 1. Кольцом называется множество математических объектов, в котором определены два действия − "сложение" и "умножение", которые сопоставляют упорядоченным парам элементов их "сумму" и "произведение", являющиеся элементами того же множества. Данные действия удовлетворяют следующим требованиям:
1. a+b=b+a (коммутативность сложения).
|
|
|
2. (a+b)+c=a+(b+c) (ассоциативность сложения).
3. Существует нулевой элемент 0 такой, что a +0= a, при любом a.
4. Для любого a существует противоположный элемент − a такой, что a +(− a)=0.
5. (a+b)c=ac+bc (левая дистрибутивность).
5'. c(a+b)=ca+cb (правая дистрибутивность).
Требования 2, 3, 4 означают, что множество математических объектов образует группу, а вместе с пунктом 1 мы имеем дело с коммутативной (абелевой) группой относительно сложения.
Как видно из определения, в общем определении кольца на умножения не накладывается никаких ограничений, кроме дистрибутивности со сложением. Однако при различных ситуациях возникает необходимость рассматривать кольца с дополнительными требованиями.
6. (ab)c=a(bc) (ассоциативность умножения).
7. ab=ba (коммутативность умножения).
8. Существование единичного элемента 1, т.е. такого a ·1=1· a=a, для любого элемента a.
9. Для любого элемента элемента a существует обратный элемент a −1 такой, что aa −1= a −1 a= 1.
В различных кольцах 6, 7, 8, 9 могут выполняться как отдельно так и в различных комбинациях.
Кольцо называется ассоциативным, если выполняется условие 6, коммутативным, если выполнено условие 7, коммутативным и ассоциативным если выполнены условия 6 и 7. Кольцо называется кольцом с единицей, если выполнено условие 8.
Примеры колец:
1. Множество квадратных матриц.
Действительно. Выполнение пунктов 1-5, 5' очевидна. Нулевым элементом является нулевая матрица. Кроме этого выполняется пункт 6 (ассоциативность умножения), пункт 8 (единичным элементом является единичная матрица). Пункты 7 и 9 не выполняются т.к. в общем случае умножение квадратных матриц некоммутативна, а также не всегда существует обратное к квадратной матрице.
2. Множество всех комплексных чисел.
3. Множество всех действительных чисел.
4. Множество всех рациональных чисел.
5. Множество всех целых чисел.
Определение 2. Всякая система чисел, содержащая сумму, разность и произведение любых двух своих чисел, называется числовым кольцом.
Примеры 2-5 являются числовыми кольцами. Числовыми кольцами являются также все четные числа, а также все целые числа делящихся без остатка на некоторое натуральное число n. Отметим, что множество нечетных чисел не является кольцом т.к. сумма двух нечетных чисел является четным числом.
Делители нуля
Пусть  — кольцо,
— кольцо,  . Числа
. Числа  называются делителями нуля кольца
называются делителями нуля кольца  , причем
, причем  — левый делитель нуля,
— левый делитель нуля,  — правый делитель нуля.
— правый делитель нуля.
Пример 1:
 — кольцо непрерывных функций на промежутке
— кольцо непрерывных функций на промежутке  .
.





Пример 2:
Пусть дано 

 =
= 

Из равенства видно, что в кольце 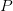 присутствуют делители нуля. Как следствие этого, мы можем наблюдать невозможность сокращения обоих частей равенства, так как это приведет нас к неверному равенству, то есть в кольце
присутствуют делители нуля. Как следствие этого, мы можем наблюдать невозможность сокращения обоих частей равенства, так как это приведет нас к неверному равенству, то есть в кольце 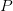 не действует закон сокращения. Если же в кольце
не действует закон сокращения. Если же в кольце 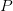 нет делителей нуля, то
нет делителей нуля, то
 — закон сокращения.
— закон сокращения.
12. 2. Гомоморфизмы и изоморфизмы колец. Идеалы.


Идеал (алгебра)
Русский
ПРАВИТЬ
ПОДЕЛИТЬСЯ
Идеал — специального рода подобъект в некоторой алгебраической структуре. Понятие идеала возникло первоначально в теории колец. Название «идеал» ведет свое происхождение от «идеальных чисел» (дивизоров).
Содержание
[развернуть]
ОпределенияПравить
Для алгебры или кольца A идеал есть подалгебра или подкольцо, замкнутая относительно умножения на элементы из A. При этом идеал называется левым (соответственно правым), если он замкнут относительно умножения слева (соответственно справа) на элементы из A. Идеал, являющийся одновременно левым и правым, называется двусторонним. В коммутативном случае все эти три понятия совпадают.
Более точно: Идеалом кольца A называется такое подмножество I кольца A, что
1. для любых элементов i и j из I, их сумма i+j также лежит в I;
2. для любого элемента i из I его противоположный элемент -i также лежит в I;
3. (условие на правые идеалы) для любого элемента i из I и любого элемента a из A произведение ia также лежит в I;
4. (условие на левые идеалы) для любого элемента i из I и любого элемента a из A произведение ai также лежит в I.
СвойстваПравить
§ Двусторонние идеалы в кольцах и алгебрах играют ту же роль, что и нормальные подгруппы в группах:
§ Для всякого гомоморфизма f: A → B ядром Ker f является идеал, и обратно, всякий идеал — ядро некоторого гомоморфизма.
§ Более того, идеал однозначно (с точностью до изоморфизма) определяет образ гомоморфизма, ядром которого он является: f (A) изоморфен факторкольцу (факторалгебре) A / I.
Для любого подмножества X ∈ A можно определить идеал IX, порождённый X, как пересечение всех идеалов, содержащих множество X. В этом случае множество X назывется базисом идеала IX. Разные базисы могут порождать один и тот же идеал. Идеал, порождённый одним элементом, называется главным.
§ Пересечение левых (двусторонних) идеалов снова будет левым (двусторонним) идеалом.
§ Для колец и алгебр теоретико-множественное объединение идеалов не обязано быть идеалом.
Пусть I, J — левые или двусторонние идеалы в кольце (или алгебре) A. Суммой идеалов I и J называется минимальный идеал в A, содержащий I и J. Относительно суммы все (левые или двусторонние) идеалы кольца (или алгебры) образуют решётку.
§ Для k -алгебры A (алгебры над полем k) идеал кольца A может, вообще говоря, не быть идеалом алгебры A.
Например, если A есть k -алгебра с нулевым умножением, то множество всех идеалов кольца A совпадает с множеством всех подгрупп аддитивной группы A, а множество всех идеалов алгебры A совпадает с множеством всех подпространств векторного k -пространства A. Однако в случае, когда A — алгебра с единицей, оба эти понятия совпадают.
12. 3. Поле. Кольца и поля вычетов.


Кольцо вычетов
Сравнение по модулю натурального числа — отношение эквивалентности на множестве целых чисел, связанное с делимостью. Оно даёт возможность работать с системой чисел, более простой чем целые числа, в которой значения «зацикливаются» (повторяются) после достижения определенного значения.

Пусть  множество всех остатков от деления целых чисел на натуральное число
множество всех остатков от деления целых чисел на натуральное число  , т. е.
, т. е.  . Суммой (произведением) двух элементов будем считать остаток от деления этой суммы (произведения) на число
. Суммой (произведением) двух элементов будем считать остаток от деления этой суммы (произведения) на число  . Рассмотрим полученную структуру
. Рассмотрим полученную структуру  .
.
ТЕОРЕМА 6. Если  составное, то
составное, то  не является полем.
не является полем.
ДОКАЗАТЕЛЬСТВО. Пусть  составное, т. е.
составное, т. е.  , где
, где  и
и  . Тогда по модулю
. Тогда по модулю  получаем
получаем 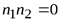 , но
, но  и
и  . Так как в поле такого быть не может (теорема 5), то при составном
. Так как в поле такого быть не может (теорема 5), то при составном  остатки с операциями по модулю
остатки с операциями по модулю  не образуют поля. □
не образуют поля. □
Покажем теперь, что в случае простого  ,
,  является полем. Вначале заметим следующее. Пусть
является полем. Вначале заметим следующее. Пусть  и
и 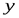 — два целых числа,
— два целых числа,  - остатки от деления их на
- остатки от деления их на  , т. е.
, т. е.  и
и  . Тогда
. Тогда  и
и  , откуда получаем, что числа
, откуда получаем, что числа  и
и  , а также числа
, а также числа 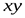 и
и  дают при делении на
дают при делении на  одинаковые остатки. Другими словами, мы получим одинаковый результат, если сначала возьмем остатки от деления
одинаковые остатки. Другими словами, мы получим одинаковый результат, если сначала возьмем остатки от деления  и
и 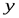 на
на  и потом сложим (или умножим) их по модулю
и потом сложим (или умножим) их по модулю  , или, если мы сначала сложим (или умножим)
, или, если мы сначала сложим (или умножим)  и
и  , как обычные натуральные числа, а затем возьмем остаток от деления полученного числа на
, как обычные натуральные числа, а затем возьмем остаток от деления полученного числа на  . Таким образом, при вычислении некоторого выражения с операциями по модулю
. Таким образом, при вычислении некоторого выражения с операциями по модулю  можно не брать остаток от деления на
можно не брать остаток от деления на  после каждой операции, а произвести вычисления сначала как с обычными натуральными числами и обычными операциями и только в конце взять остаток от деления полученного числа на
после каждой операции, а произвести вычисления сначала как с обычными натуральными числами и обычными операциями и только в конце взять остаток от деления полученного числа на  . Это позволяет утверждать, что операции сложения и умножения ассоциативны и коммутативны, а также справедлива дистрибутивность умножения относительно сложения.
. Это позволяет утверждать, что операции сложения и умножения ассоциативны и коммутативны, а также справедлива дистрибутивность умножения относительно сложения.
Нейтральным элементом по сложению является  , а единичным элементом по умножению-
, а единичным элементом по умножению-  . Остается показать, что при
. Остается показать, что при  простом у каждого остатка
простом у каждого остатка  , отличного от
, отличного от  , есть обратный, т. е. что найдется остаток
, есть обратный, т. е. что найдется остаток  такой, что
такой, что 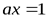 по модулю
по модулю  . Итак, пусть
. Итак, пусть  . Рассмотрим числа
. Рассмотрим числа
 (умножение обычное).
(умножение обычное).
Разность любых двух из этих чисел  не делится на
не делится на  , так как
, так как  простое, а
простое, а  и
и  . Таким образом, все эти
. Таким образом, все эти  чисел дают разные и, следовательно, всевозможные остатки при делении на
чисел дают разные и, следовательно, всевозможные остатки при делении на  . Значит, одно из этих чисел дает при делении на
. Значит, одно из этих чисел дает при делении на  остаток
остаток  , т. е.
, т. е.  по модулю
по модулю  для некоторого остатка
для некоторого остатка  .
.
Таким образом, при  простом все свойства поля выполняются.
простом все свойства поля выполняются.
12. 4. Характеристика поля. Конечные поля.
Характеристика (кольца или поля) — числовая величина, используемая в общей алгебре для описания некоторых свойств этих алгебраических структур.


12. 5. Вычисления в конечных кольцах и полях (вычетов).
?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
|
|
|


