К термину «Вероятность безотказной работы» (п. 6.8)

Вероятность безотказной работы определяется в предположении, что в начальный момент времени (момент начала исчисления наработки) объект находился в работоспособном состоянии. Обозначим через t время или суммарную наработку объекта (в дальнейшем для краткости называем (просто наработкой). Возникновение первого отказа — случайное событие, а наработка т от начального момента до возникновения этого события — случайная величина. Вероятность безотказной работы Р(t) объекта в интервале от 0 до t включительно определяют как

. (1)

Здесь Р{•}— вероятность события, заключенного в скобках. Вероятность безотказной работы P (t) является функцией наработки t. Обычно эту функцию предполагают непрерывной и дифференцируемой.

Если способность объекта выполнять заданные функции характеризуется одним параметром v, то вместо (1) имеем формулу

, (2)

где v_* и v_**— предельные по условиям работоспособности значения параметров (эти значения, вообще, могут изменяться во времени).

Аналогично вводят вероятность безотказной работы в более общем случае, когда состояние объекта характеризуется набором параметров с допустимой по условиям работоспособности областью значений этих параметров [8].

Вероятность безотказной работы Р(t) связана с функцией распределения F(t) и плотностью распределения f(t) наработки до отказа:

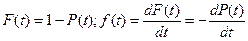. (3)

С. 30 ГОСТ 27.002—89

Наряду с понятием «вероятность безотказной работы» часто используют понятие «вероятность отказа», которое определяется следующим образом: это вероятность того, что объект откажет хотя бы один раз в течение заданной наработки, будучи работоспособным в начальный момент времени. Вероятность отказа на отрезке от 0 до t определяют по формуле

. (4)

Точечные статистические оценки для вероятности безотказной работы от 0 до t и для функции распределения наработки до отказа даются формулами:

, (5)

где N — число объектов, работоспособных в начальный момент времени;

п(t) — число объектов, отказавших на отрезке от 0 до t.

Для получения достоверных оценок объем выборки N должен быть достаточно велик [2, 3, 7].

Определение безотказной работы в соответствии с формулами (1) и (2) относится к объектам, которые должны функционировать в течение некоторого конечного отрезка времени. Для объектов одноразового (дискретного) применения вероятность безотказной работы определяют как вероятность того, что при срабатывании объекта отказ не возникает. Аналогично вводят вероятность безотказного включения (например в рабочий режим из режима ожидания).

К терминам «Гамма-процентная наработка до отказа», «Гамма-процентный ресурс», «Гамма-процентный срок службы», «Гамма-процентное время восстановления», «Гамма-процентный срок сохраняемости» (пп. 6.9; 6.15; 6.20; 6.24)

Перечисленные показатели определяют как корни t_γ уравнения

, (6)

где F (t) — функция распределения наработки до отказа (ресурса, срока службы).

В частности, гамма-процентную наработку до отказа t_γ определяют из уравнения

,

где Р(t) — вероятность безотказной работы.

Как видно из формулы (6), гамма - процентные показатели равны квантилям соответствующих распределений. Если вероятности, отвечающие этим квантилям, выражают в процентах, то для показателей безотказности обычно задают значения 90; 95; 99; 99,5% и т. д. Тогда вероятность возникновения отказа на отрезке [0; t] будет составлять 0,10; 0,05; 0,01; 0,005 и т. д. Задаваемые значения γ для критических отказов должны быть весьма близки к 100%, чтобы сделать критические отказы практически невозможными событиями. Для прогнозирования потребности в запасных частях, ремонтных мощностях, а также для расчета пополнения и обновления парков машин, приборов и установок могут потребоваться гамма - процентные показатели при более низких

ГОСТ 27.002—89 С. 31

значениях γ, например при γ = 50%, что приближенно соответствует средним значениям.

Статистические оценки для гамма-процентных показателей могут быть по­лучены на основе статистических оценок либо непосредственно, либо после аппроксимации эмпирических функций подходящими аналитическими распре­делениями. Необходимо иметь в виду, что экстраполирование эмпирических результатов за пределы продолжительности испытаний (наблюдений) без при­влечения дополнительной информации о физической природе отказов может привести к значительным ошибкам.

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: