 |
Определение расходов воды аналитическим способом
|
|
|
|
Цель занятия - вычислить расход воды аналитическим способом по скоростям, измеренным гидрологической вертушкой и глубинам потока.
Задачи
1) освоить основные понятия гидрометрии;
2) определить ширину реки;
3) определить расход воды;
4) определить площадь живого сечения;
5) определить среднюю и максимальную скорость течения реки;
6) определить среднюю и максимальную глубину реки;
7) определить смоченный периметр и гидравлический радиус.
Исходные данные: выписка из книжки для записи изменения расхода на реке Олха (таблица 3.1 столбцы 1,2,3,4 и 9).
Требуется: вычислит расход воды (Q), смоченный периметр дна (χ); площадь живого сечения реки (w); ширину реки (В), среднюю глубину реки (hср), максимальную глубину реки (hmax), среднюю и максимальную скорость течения реки (v) и (vmax), гидравлический радиус (R).
Порядок выполнения задания
1) определяют средние глубины между промерными вертикалями как среднее арифметическое средних глубин (0+0,52)/2=0,26; (0,52+0,87)/2=0,69; (0,87+1,38)/2=1,11; (1,36+1,74)/2=1,55; (1,74+2,02)/2=1,88; (2,02+2,35)/2=2,18; (2,35+1,97)/2=2,16; (1,97+1,52)/2=1,74; (1,52+0,58)/2=1,05; (0,58+0)/2=0,29; заполняется столбец 5;
2) находят расстояние между промерными вертикалями, используя разницу между расстояниями от постоянного начала (столбец 6): 5-7=2; 7-5=2; 9-7=2; 11-9=2; 13-11=2; 15-13=2; 17-15=2; 19-17=2; 21-19=2; 24,9-21=3,9
3) вычисляют площади живого сечения между промерными вертикалями (столбец 7): 0,26∙2=0,52; 0,69∙2=1,38; 1,11∙2=2,22; 1,55∙2=3,10; 1,88∙2=3,76;
2,18∙2=4,36; 2,16∙2=4,32; 1,74∙2=3,48; 1,05∙2=2,10; 0,29∙3,9=1,13;
4) вычисляют площади живого сечения между скоростными вертикалями (столбец 8): 0,52+1,38=1,90; 2,22+3,10+3,76=9,08; 4,36+4,32=8,68; 3,48+2,10+1,13=6,71;
5) по данным столбца 9 вычисляются средние скорости между скоростными вертикалями (столбец 10) (к=0,7): 0,74∙0,7=0,52; (0,74+0,89)/2=0,81; (0,89+0,78)/2=0,83; 0,78∙0,7=0,54;
|
|
|
6) расходы воды между скоростными вертикалями (столбец 11) находят путем умножения значений столбца 8 и 10 (произведение площади живого сечения между скоростными вертикалями и средней скоростью между скоростными вертикалями): 1,90∙0,52=0,98; 9,08∙0,81=7,35; 8,68∙0,83=7,20; 6,71∙0,54=3,62;
7) сумма значений 7 и 8 столбца представляет собой площадь живого сечения – 26,3 м2;
Таблица 3.1 – Расчет расхода воды реки Олха аналитическим способом
| № вертикалей | Расстояние от постоянного начала, м | Глубина, м | Расстояние между промерными вертикалями | Площадь живого сечения, м2 | Средняя скорость, м/с2 | Расход воды между скоростными вертикалями, м3./с | ||||
| Промерных | Скоростных | средняя | между промерными вертикалями | между промерными вертикалями | между скоростными вертикалями | На вертикали | между скоростными вертикалями | |||
| Урез пб | ||||||||||
| 0,26 | 0,52 | 1,90 | 0,52 | 0,98 | ||||||
| 0,52 | ||||||||||
| 0,69 | 1,38 | |||||||||
| I | 0,87 | |||||||||
| 1,11 | 2,22 | 9,08 | 0,74 | 0,81 | 7,35 | |||||
| 1,36 | ||||||||||
| 1,55 | 3,10 | |||||||||
| 1,74 | ||||||||||
| 1,88 | 3,76 | |||||||||
| II | 2,02 | |||||||||
| 2,18 | 4,36 | 8,68 | 0,89 | 0,83 | 7,20 | |||||
| 2,35 | ||||||||||
| 2,16 | 4,32 | |||||||||
| III | 1,97 | |||||||||
| 1,74 | 3,48 | 6,71 | 0,78 | 0,54 | 3,62 | |||||
| 1,52 | ||||||||||
| 1,05 | 2,10 | |||||||||
| 0,58 | ||||||||||
| 0,29 | 3,9 | 1,13 | ||||||||
| Урез лб | 24,9 | |||||||||
| Итого: | 26,3 | 19,1 |
|
|
|
8) сумма последнего столбца соответствует значению расхода воды – 19,1м3/с.
Вычислим дополнительные гидрометрические характеристики реки Олха.
Средняя скорость (vср) рассчитывается по следующей формуле:
 (3.1)
(3.1)
где Q – общий расход воды, м3/с;  – площадь живого сечения, м2.
– площадь живого сечения, м2.

Средняя глубина реки (hср) рассчитывается по формуле
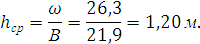
где  – площадь живого сечения, м2, В – ширина реки, м.
– площадь живого сечения, м2, В – ширина реки, м.
Смоченный периметр, рассчитывается по формуле:

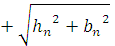 (3.2)
(3.2)
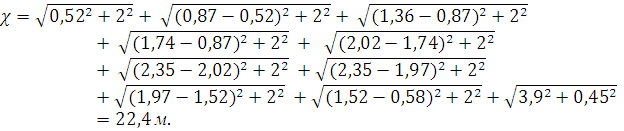
Гидравлический радиус рассчитывается по формуле:
 (3.3)
(3.3)
где  – площадь живого сечения, м2, χ – смоченный периметр, м.
– площадь живого сечения, м2, χ – смоченный периметр, м.

Ширина реки определяется как расстояние между урезом левого и урезом правого берегов: В=21,9
Наибольшая глубина выбирается из столбца 4 таблицы 3.1

Наибольшая скорость течения выбирается из столбца 9 таблицы 3.1

В таблице 3.2 приведены результаты вычисления характеристик реки Олха.
Таблица 3.2 – Расчет гидрометрических характеристик реки Олха
| Q, м3/с | ω, м2 | hmax, м | hср, м | В, м | R, м |  , м/с , м/с
| χ, м | 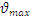 , м/с , м/с
|
| 18,5 | 27,3 | 2,35 | 1,25 | 21,9 | 1,17 | 0,68 | 22,4 | 0,95 |
Вывод. Таким образом, на основе аналитического метода по определению расхода воды получена таблица, в которой приведены гидрометрические характеристики. Расход воды, полученный аналитическим способом, составил 19,1 м3/с.
Расчет годового стока
Цель работы: рассмотреть факторы формирования годового стока и изучить методы расчета годового стока реки: при наличии, недостаточности и отсутствии данных.
Задачи расчета годового стока при наличии данных наблюдений:
- изучить факторы формирования годового стока;
- построить эмпирическую функцию распределения;
- найти статистические параметры гидрологического ряда;
- определить абсолютные и относительные погрешности;
- построить нормальный закон и гамма-функцию распределения;
- определить расход воды заданной вероятности превышения.
Исходные данные: среднегодовые расходы воды реки Олха (с. Олха) по данным наблюдений за 26 лет.
|
|
|
Требуется: 1) построить эмпирическую и аналитические функции распределения (нормальный и гамма-распределения); 2) выбрать приемлемый закон распределения согласно критерию χ2, или Колмогорова; 3) определить расход воды с вероятностью превышения Р=80%.
Порядок выполнения задания
1. В первом и втором столбце таблицы 4.1 приведены годы (n=26 лет) и среднегодовой расход воды реки Олха.
2. В третьем столбце приведены порядковые номера среднегодового расхода реки.
3. В шестом столбце рассчитываем модульные коэффициенты  где Q – значение среднегодового расхода воды,
где Q – значение среднегодового расхода воды,  - среднее значение ряда, которое предварительно рассчитывается по значениям столбца 2. В данном примере
- среднее значение ряда, которое предварительно рассчитывается по значениям столбца 2. В данном примере  =12,8 м3/с. Таким образом,
=12,8 м3/с. Таким образом,  вычисляется следующим образом:
вычисляется следующим образом:

и т. д.
Таблица 4.1 – Вычисление эмпирической обеспеченности среднегодовых расходов воды реки Олха (с. Олха)
| Годы | Q, м³/с | № | Q, м³/с | Pi, % | Кi |
| 15,0 | 16,2 | 3,70 | 1,17 | ||
| 15,2 | 15,2 | 7,41 | 1,19 | ||
| 11,7 | 15,1 | 11,1 | 0,91 | ||
| 14,2 | 15,0 | 14,8 | 1,11 | ||
| 13,0 | 14,8 | 18,5 | 1,02 | ||
| 11,5 | 14,7 | 22,2 | 0,90 | ||
| 11,4 | 14,5 | 25,9 | 0,89 | ||
| 16,2 | 14,2 | 29,6 | 1,27 | ||
| 14,2 | 14,2 | 33,3 | 1,11 | ||
| 13,6 | 14,2 | 37,0 | 1,06 | ||
| 13,0 | 13,6 | 40,7 | 1,02 | ||
| 15,1 | 13,3 | 44,4 | 1,18 | ||
| 13,3 | 13,2 | 48,1 | 1,04 | ||
| 12,0 | 13,0 | 51,8 | 0,94 | ||
| 14,2 | 13,0 | 55,5 | 1,11 | ||
| 14,7 | 12,0 | 59,2 | 1,15 | ||
| 11,3 | 11,7 | 62,9 | 0,88 | ||
| 10,2 | 11,5 | 66,6 | 0,80 | ||
| 9,30 | 11,4 | 70,3 | 0,73 | ||
| 10,4 | 11,3 | 74,0 | 0,81 | ||
| 10,6 | 10,6 | 77,7 | 0,83 | ||
| 10,1 | 10,4 | 81,4 | 0,79 | ||
| 14,5 | 10,3 | 85,1 | 1,13 | ||
| 10,33 | 10,2 | 88,9 | 0,81 | ||
| 14,8 | 10,1 | 92,6 | 1,16 | ||
| 13,2 | 9,30 | 96,3 | 1,03 |
4. В пятом столбце записываются вычисления эмпирической вероятности превышения
 (4.1)
(4.1)
где m – порядковый номер (столбец 3).

5. В столбце Q м3/с, которые располагаются в порядке убывания.
6. По данным эмпирической вероятности превышения Pi, и ранжированному ряду Q, м3/с строится эмпирическая функция распределения среднегодовых расходов воды реки (рисунок 4.1.)

Рисунок 4.1 – Эмпирическая функция распределения среднегодовых расходов воды реки Олха (с. Олха) за период 1959 - 1984 гг.
|
|
|
7. По среднегодовым расходам воды с помощью MS Excel (описательная статистика) получены статистические параметры годового стока (таблица 4.2).
Таблица 4.2 – Статистические параметры годового стока реки Олха (с. Олха)
| Среднее | 12,8 |
| Стандартная ошибка | 0,38 |
| Медиана | 13,1 |
| Мода | 14,2 |
| Стандартное отклонение | 1,96 |
| Дисперсия выборки | 3,83 |
| Эксцесс | -1,23 |
| Асимметричность | -0,16 |
| Интервал | 6,90 |
| Минимум | 9,30 |
| Максимум | 16,2 |
| Сумма | |
| Счет | 26,0 |
В дополнение к этим параметрам рассчитываются коэффициент вариации Сv по формуле
 (4.2)
(4.2)
 .
.
8. Помимо статистических параметров рассчитывается стандартные погрешности среднего значения, коэффициента вариации и коэффициента асимметрии по формулам
 (4.3)
(4.3)
 (4.4)
(4.4)
 (4.5)
(4.5)
 (4.6)
(4.6)
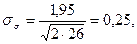
 ,
,

Для определения относительных значений погрешностей статистических параметров (5.15)-(5.17) необходимо полученные результаты разделить на значение параметров (Q, Сv, Сs)
 (4.7)
(4.7)
 (4.8)
(4.8)
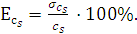 (4.9)
(4.9)



Относительное значение  можно не учитывать, так как асимметричность сs
можно не учитывать, так как асимметричность сs
очень мала.
9. Аналитические функции распределения вероятностей среднегодовых расходов воды строим, используя нормальный закон и гамма-распределение.
Расчетное значение функции распределения нормального Рн и гамма-распределения Рг приведены в 6 и 7 столбце таблицы 4.3, а остальные данные в убывающем порядке перенесены из таблицы 4.1.
Для определения Рн и Рг использованы функции табличного процессора MS Excel:
=(1-НОРМРАСП(Кр;1;Сv;1))*100,
=(1-ГАММАРАСП(Кр;1/Cv^2;Сv^2;1))*100
В приведенных функциях Кр представляет собой ячейку со значением модульного коэффициента (Кр=1,27; Кр=1,19;…. Кр=0,73), Сv-коэффициент вариации (0,15).
Таблица 4.3 – Расчет параметров аналитической кривой обеспеченности среднегодовых расходов воды реки Олха (с. Олха)
| № | Годы | Q, м³/с | Kр | Р, % | Рн, % | Рг, % |
| 16,2 | 1,27 | 3,70 | 3,83 | 4,61 | ||
| 15,2 | 1,19 | 7,41 | 10,5 | 10,9 | ||
| 15,1 | 1,18 | 11,1 | 11,5 | 11,8 | ||
| 15,0 | 1,17 | 14,8 | 12,5 | 12,8 | ||
| 14,8 | 1,16 | 18,5 | 14,8 | 14,8 | ||
| 14,7 | 1,15 | 22,2 | 16,1 | 16,0 | ||
| 14,5 | 1,13 | 25,9 | 18,8 | 18,4 | ||
| 14,2 | 1,11 | 29,6 | 23,2 | 22,5 | ||
| 14,2 | 1,11 | 33,3 | 23,2 | 22,5 | ||
| 14,2 | 1,11 | 37,0 | 23,2 | 22,5 | ||
| 13,6 | 1,06 | 40,7 | 33,8 | 32,3 | ||
| 13,3 | 1,04 | 44,4 | 39,7 | 37,9 | ||
| 13,2 | 1,03 | 48,1 | 41,7 | 39,8 | ||
| 13,0 | 1,02 | 51,8 | 45,8 | 43,9 | ||
| 13,0 | 1,02 | 55,5 | 45,8 | 43,9 | ||
| 12,0 | 0,94 | 59,2 | 66,1 | 64,6 | ||
| 11,7 | 0,91 | 62,9 | 71,6 | 70,5 | ||
| 11,5 | 0,90 | 66,6 | 75,0 | 74,2 | ||
| 11,4 | 0,89 | 70,3 | 76,7 | 76,0 | ||
| 11,3 | 0,88 | 74,0 | 78,2 | 77,7 | ||
| 10,6 | 0,83 | 77,7 | 87,4 | 87,8 | ||
| 10,4 | 0,81 | 81,4 | 89,4 | 90,1 | ||
| 10,3 | 0,81 | 85,1 | 90,0 | 90,8 | ||
| 10,2 | 0,80 | 88,8 | 91,2 | 92,0 | ||
| 10,1 | 0,79 | 92,5 | 92,0 | 92,9 | ||
| 9,30 | 0,73 | 96,3 | 96,5 | 97,5 | ||
 12,8 12,8
|
|
|
|
10. По данным столбцов (4 и 5) строим эмпирическую и аналитические функции распределения рисунок (4.2).

Рисунок 4.2 – Эмпирическая функция (Р, %), нормальный закон распределения (Рн, %) и гамма-распределение (Рг, %) модульных коэффициентов годового стока реки Олха (с. Олха) за период 1959-1984 гг.
11. Расход воды обеспеченностью 80% при нормальном законе распределения и при законе гамма-распределения рассчитывается по формулам (4.10) и (4.11).
Q80н=к80н·  , м3/с, (4.10)
, м3/с, (4.10)
Q80г=к80г·  , м3/с. (4.11)
, м3/с. (4.11)
Q80н=0,87 ·12,8=11,2 м3/с,
Q80г=0,87·12,8=11,2 м3/с.
Значения К80н, К80г получают при помощи Excel, применив функции ГАММАОБР и НОРМОБР.
=НОРМОБР(1-0,80;1;Сv),
=ГАММАОБР(1-0,80;1/Сv^2;Cv^2).
=НОРМОБР(1-0,80;1;0,15)=0,87,
=ГАММАОБР(1-0,80;1/0,15^2;0,15^2)=0,87.
12. Согласно таблице 4.4 определяется максимальное значение расхождения между вероятностями распределения (столбец 4 и 5). По максимальному значению расхождения (Д) определяется эмпирическое значение критерия Колмогорова для нормального закона и гамма-распределения.
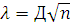 (4.12)
(4.12)
Таблица 4.4 – Выбор значимого закона распределения вероятности реки Олха (с. Олха)
| Р, % | Рн, % | Рг, % | |P-Pн| | |P-Pг| |
| 3,70 | 3,83 | 4,61 | 0,13 | 0,91 |
| 7,41 | 10,5 | 10,9 | 3,16 | 3,55 |
| 11,1 | 11,5 | 11,8 | 0,44 | 0,75 |
| 14,8 | 12,5 | 12,8 | 2,22 | 2,00 |
| 18,5 | 14,8 | 14,8 | 3,64 | 3,63 |
| 22,2 | 16,1 | 16,0 | 6,10 | 6,21 |
| 25,9 | 18,8 | 18,4 | 7,13 | 7,48 |
| 29,6 | 23,2 | 22,5 | 6,33 | 7,08 |
| 33,3 | 23,2 | 22,5 | 10,0 | 10,8 |
| 37,0 | 23,2 | 22,5 | 13,7 | 14,5 |
| 40,7 | 33,8 | 32,3 | 6,89 | 8,40 |
| 44,4 | 39,7 | 37,9 | 4,72 | 6,50 |
| 48,1 | 41,7 | 39,8 | 6,40 | 8,25 |
| 51,8 | 45,8 | 43,9 | 6,00 | 7,96 |
| 55,5 | 45,8 | 43,9 | 9,70 | 11,6 |
| 59,2 | 66,1 | 64,6 | 6,89 | 5,37 |
| 62,9 | 71,6 | 70,5 | 8,70 | 7,57 |
| 66,6 | 75,0 | 74,2 | 8,42 | 7,58 |
| 70,3 | 76,7 | 76,0 | 6,33 | 5,65 |
| 74,0 | 78,2 | 77,7 | 4,19 | 3,67 |
| 77,7 | 87,4 | 87,8 | 9,63 | 10,1 |
| 81,4 | 89,4 | 90,1 | 7,95 | 8,62 |
| 85,1 | 90,0 | 90,8 | 4,90 | 5,62 |
| 88,8 | 91,2 | 92,0 | 2,33 | 3,15 |
| 92,5 | 92,0 | 92,9 | 0,58 | 0,31 |
| 96,3 | 96,5 | 97,5 | 0,29 | 1,27 |
| 0,14 | 0,14 |
λн=0,14*КОРЕНЬ(26)=0,70
λГ=0,14*КОРЕНЬ(26)=0,74
Для уровня значимости α по таблице 4.5 получаем теоретическое значение λα. Полученные результаты сравниваем с 0,05 в табличном значение которое составляет 1,358.
Таблица 4.5 – Критические значения λα для распределения Колмогорова
| Α | 0,5 | 0,4 | 0,3 | 0,2 | 0,1 |
| λα | 0,828 | 0,895 | 0,974 | 1,073 | 1,224 |
| Α | 0,05 | 0,02 | 0,01 | 0,001 | |
| λα | 1,358 | 1,52 | 1,627 | 1,95 |
Согласно полученным результатам оба значения 0,70 и 0,74 соответствуют, табличным значениям и не превышают 1,358.
Вывод. В ходе работы были рассчитаны характеристики годового стока р. Олха (с. Олха) за период с 1959-1984 гг., так же составлена описательная статистика, и на основании данных построена эмпирическая кривая обеспеченности среднегодовых расходов воды за рассмотренные годы. Получены следующие данные: Q80н=11,2 м3/с (нормальный закон распределения), Q80г=11,2 м3/с(гамма-распределение). Получившиеся данные по двум законам распределения совпадают по значениям.
|
|
|


