 |
Пример выполнения контрольной работы по теме «Тема 1.3. Численное интегрирование»
|
|
|
|
Контрольные задания по теме
«Тема 1.4. Численное интегрирование»
Общее задание
1. Получить вариант задания и номера задач в нем.
Определить значение интеграла с использованием заданного численного метода.
Если по условию подынтегральная функция задана таблицей с не равноотстоящими узлами, то для получения дополнительного узла следует использовать линейную интерполяцию.
Оценить погрешность интегрирования с использованием правила Рунге.
Получить точное значение интеграла аналитическими методами.
Оценить погрешность численного интегрирования, путем сравнения точного и приближенного значений определенного интеграла.
Вычислить значение интеграла с использованием средств заданного математического пакета.
Сравнить полученные результаты.
Варианты контрольной работы по теме «Численное интегрирование»
Вариант № 1
1. Определить значение интеграла, вычисленное с использованием формулы трапеции, для функции, заданной таблично,
| x | 0,1 | 0,2 | 0,3 | 0,4 |
| y(x) | -4 | -3,8 |
2. Оценить погрешность, при вычислении определенного интеграла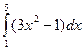 
по формуле левых прямоугольников с шагом h=1.
Вариант № 2
1. Определить значение интеграла для функции, заданной таблично, вычисленного методом Симпсона
| x | |||||
| y(x) |
2. Оценить погрешность интегрирования по правилу Рунге при вычислении интеграла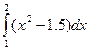 
методом средних прямоугольников с h=1 и h=0.5.
Вариант № 3
1. Определить значения интеграла 
, вычисленного по формуле правых прямоугольников, если подынтегральная функция задана таблицей.
| x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| y(x) | 5.5 | 4,5 | 3,5 |
2. Вычислить значения интеграла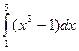 
с шагом h=1 методами правых и левых прямоугольников и оценить их погрешности.
|
|
|
Вариант № 4
1. Значения интеграла 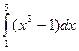вычисленного с шагом h=1, соответственно, методами правых и левых прямоугольников, равны...Определить значения интеграла 
, вычисленного по формуле левых прямоугольников, если подынтегральная функция задана таблицей.
| x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| y(x) | 3,5 |
2. Оценить погрешность значения интеграла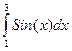 
, вычисленного по методу трапеций с h=2 и h=1, по правилу Рунге.
Вариант № 5
1. Определить значения интеграла вычисленного с использованием формулы Симпсона от функции 
на отрезке [1; 5] с шагом h=2.
2. Вычислить значения интеграла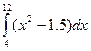 
с шагом h=2 методом средних прямоугольников и провести оценку погрешности результата.
Вариант № 6
1. Определить Значения интеграла вычисленного с использованием метода трапеций от функции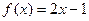 
на интервале [0.1;0.7] с шагом 0,1.
2. Вычислить значения интеграла от функции, заданной таблично, методом трапеций (для вычисления значения функции в точке 2 использовать линейную интерполяцию)
| x | |||
| ƒ(х) |
Вариант № 7
1. Определить значение определенного интеграла 
, вычисленного по формуле трапеций с шагом h=1.
2. Оценить погрешность значения интеграла 
, вычисленного по методу трапеций с h=2 и h=1, по правилу Рунге.
Вариант № 8
1. Определить значение определенного интеграла 
, вычисленного по формуле правых прямоугольников с шагом интегрирования h=1.
2. Оценить погрешность значения интеграла, вычисленного по методу левых прямоугольников с h=0.2 и h=0.1, если функция задана таблично, по правилу Рунге
| x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| ƒ(х) | -2.5 | -2 | 0,5 | 1,5 |
Вариант № 9
1. Определить значение интеграла, вычисленного по формуле левых прямоугольников для функции, заданной таблично.
| х | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| ƒ(х) | -0,68 | -0,32 | 0,08 | 0,52 |
2. Оценить погрешность, полученную при вычислении определенного интеграла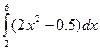 
по формуле трапеций с шагом h=2.
|
|
|
Вариант № 10
1. Определить значение интеграла 
, вычисленного по формуле левых прямоугольников с шагом h=0.5.
2. Оценить погрешность значения интеграла 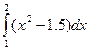, вычисленного по методу средних прямоугольников с h=1 и h=0.5, по правилу Рунге.
Вариант № 11
1. Определить значение интеграла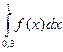 
, вычисленного с использованием формулы трапеций,при табличном задании подынтегральной функции
| x | 0,3 | 0,6 | 0,9 | |
| y(x) | -0,4 | 0,1 | 1,5 |
2. Погрешность, полученная при вычислении интеграла 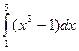методом левых прямоугольников с шагом h=1.
Вариант № 12
1. Определить значение интеграла 
, вычисленного с использованием формулы Симпсона с шагом 0.1
2. Оценить погрешность при вычислении интеграла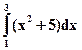 
с шагом h=1, методом средних прямоугольников.
Вариант № 13
1. Определить значение интеграла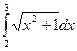 
, вычисленного по формуле средних прямоугольников с шагом h=0.5.
2. Вычислить значение интеграла от функции, заданной таблично, методом Симпсона (для вычисления значения функции в точке 2 использовать линейную интерполяцию)
| x | ||
| ƒ(х) | 0,5 | 0,2 |
Вариант № 14
1. Определить значение интеграла 
, вычисленного по формуле Симпсона при n=4.
2. Вычислить значения интеграла, вычисленного от функции, заданной таблично, методом трапеций с шагом h=0,1.
| x | 0,1 | 0,2 | 0,4 |
| ƒ(х) | -1 |
Вариант № 15
1. Определить значение интеграла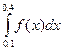 
, вычисленного с использованием формулы трапеции для функции, заданной таблично
| x | 0,1 | 0,2 | 0,3 | 0,4 |
| f(x) |
2. Оценить погрешность значения интеграла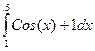 
, вычисленного по методу Симпсона с h=2 и h=1, по правилу Рунге.
Вариант № 16
1. Определить значение 
, вычисленного по формуле трапеции с шагом h=1.
2. Оценка погрешность значения интеграла, вычисленного по методу Симпсона с h=2 и h=1, если функция задана таблично, по правилу Рунге
| x | |||||
| ƒ(х) | 8.5 | 10,5 |
Вариант № 17
1. Определить значение интеграла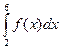 
, вычисленного с использованием формулы трапеции для функции 
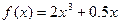с шагом h=2.
2. Оценить погрешность значения интеграла, вычисленного по методу правых прямоугольников с h=0.2 и h=0.1, если функция задана таблично, по правилу Рунге
|
|
|
| x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| ƒ(х) | 8.5 | 10,5 |
Вариант № 18
1. Определить значение интеграла 
, вычисленного с использованием формулы правых прямоугольников, для функции, заданной таблично.
| x | 2,0 | 2,3 | 2,8 | 3,3 |
| f(x) | -4 | -3,8 |
2. Оценить погрешность, при вычислении определенного интеграла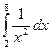 
по формуле Симпсона с шагом h=3.
Вариант № 19
1. Определить значение интеграла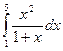 
, вычисленного с использованием формулы трапеций, если количество разбиений интервала интегрирования n=4.
2. Оценить погрешность значения интеграла 
, вычисленного по методу средних прямоугольников с h=4 и h=2, по правилу Рунге.
Вариант № 20
1. Определить значение интеграла, вычисленного по формуле Симпсона для функции, заданной таблично
| х | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| ƒ(х) | -0,68 | -0,32 | 0,08 | 0,52 |
2. Вычислить значение интеграла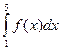 
, вычисленного методом трапеций от функции, заданной таблично, (для вычисления значения функции в точке 3 использовать линейную интерполяцию)
| x | |||
| ƒ(х) | -0,5 | -0,1 |
Вариант № 21
1. Определить значения 
, вычисленного по формуле Симпсона с шагом 2.
2. Оценить погрешность значения интеграла, вычисленного по методу левых прямоугольников с h=0.2 и h=0.1, если подынтегральная функция функции задана следующей таблицей, по правилу Рунге
| x | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 |
| ƒ(х) | -0,8 | 0,01 | 0,5 |
Вариант № 22
1. Определить значение интеграла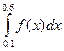 
, вычисленного по формуле трапеций для функции, заданной следующей таблицей.
| x | 0,1 | 0,2 | 0,4 | 0,6 |
| f(x) | -4 | -3,8 |
2. Оценить погрешность значения интеграла, вычисленного по методу Симпсона с h=2 и h=1, если подынтегральная функция функции задана следующей таблицей, по правилу Рунге
| x | |||||
| ƒ(х) | 0,6 | 0,2 | 0,8 | 1.5 |
Вариант № 23
1. Определить значения интегралов, вычисленных от функции, заданной таблично, методом правых прямоугольников.
| x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| ƒ(х) | -0,68 | -0,32 | 0,08 | 0,52 |
2. Оценить погрешность, при вычислении определенного интеграла 
по формуле трапеций с шагом h=1.
|
|
|
Вариант № 24
1. Определить значение интеграла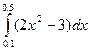 
, вычисленного по формуле трапеций с шагом h=0.1.
2. Оценить погрешность значения интеграла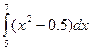 
, вычисленного по методу средних прямоугольников с h=1 и h=0.5, по правилу Рунге.
Вариант № 25
1. Определить значение интеграла 
, вычисленного по формуле Симпсона c шагом h=1.
2. Оценить погрешность значения интеграла 
, вычисленного по методу трапеций с h=2 и h=1, если подынтегральная функция, по правилу Рунге.
1.
Пример выполнения контрольной работы по теме «Тема 1.3. Численное интегрирование»
|
|
|
