 |
Задания контрольной работы
|
|
|
|
Министерство образования и науки РФ
Федеральное государственное бюджетное
Общеобразовательное учреждение
Высшего профессионального образования
«Тульский государственный университет»
КАФЕДРА МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ
ПО МАТЕМАТИКЕ (алгебре и геометрии, математическому анализу)
ДЛЯ КОНТРОЛЬНЫХ РАБОТ СТУДЕНТОВ,
ОБУЧАЮЩИХСЯ ПО ЗАОЧНОЙ ФОРМЕ
Тула 2015
Инструкция
При выполнении контрольной работы студент должен руководствоваться следующими указаниями:
1. Каждая работа должна выполняться в отдельной тетради (в клетку), на внешней обложке которой должны быть напечатано следующее (фамилия печатается или пишется большими печатными буквами)
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное общеобразовательное учреждение
высшего профессионального образования
«Тульский государственный университет»
Механико-математический факультет
КАФЕДРА МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ
Контрольная работа № ____
по дисциплине ________________________________________________
Группа __________
Фамилия __________________ Имя _________________ Отчество ________________
№ зачетной книжки ___________
№ варианта: таблица _____, вариант _____
Преподаватель: доцент Пустовгар А.С.
|
2. Студент выполняет тот вариант контрольной работы, который совпадает с последней цифрой номера зачетной книжки. Если предпоследняя цифра номера зачетной книжки есть число нечетное (1, 3, 5, 7, 9), то номера задач приводятся в таблице с нечетным номером; если же предпоследняя цифра — число четное (0, 2, 4, 6, 8), то номера задач даны в таблице с четным номером. Номера таблиц выбираются в соответствии со специальностью:
|
|
|
| Специальность | Номера таблиц |
| Все технические направления с нормативным сроком обучения, кроме направлений, указанных ниже | 1, 2 |
| Все направления сокращенной формы обучения, кроме направлений, указанных ниже | 3, 4 |
| Направление «Строительство. Городское строительство и хозяйство» сокращенной формы обучения | 5, 6 |
| Направление «Информатика и вычислительная техника. Системы автоматизированного проектирования» нормативной и сокращенной формы обучения | 7, 8 |
3. Задачи следует располагать в порядке возрастания номеров. Перед решением каждой задачи надо полностью переписать условие. Решение задач следует излагать подробно, с указанием необходимых формул.
4. Решение задач геометрического содержания должно сопровождаться чертежами, с указанием осей координат и единиц масштаба.
5. Контрольные работы должны выполняться самостоятельно. Несамостоятельно выполненная работа лишает студента возможности проверить степень своей подготовленности по теме.
6. Получив не зачтённую работу, студент должен исправить все отмеченные ошибки и недочеты. Неправильно выполненные задачи исправляются целиком в конце работы (работа над ошибками). Исправленная работа представляется на повторное рецензирование.
7. Студент допускается до экзамена при наличии зачтенной контрольной работы.
Таблица 1
| Номер варианта | Номера задач для контрольных работ | ||||||||||||||
| Работа 1 | Работа 2 | ||||||||||||||
| Номера задач для контрольных работ | |||||||||||||||
| Работа 3 | Работа 4 | ||||||||||||||
|
|
|
Таблица 2
| Номер варианта | Номера задач для контрольных работ | ||||||||||||||
| Работа 1 | Работа 2 | ||||||||||||||
| Номера задач для контрольных работ | |||||||||||||||
| Работа 3 | Работа 4 | ||||||||||||||
|
|
|
Таблица 3
| Номер варианта | Номера задач для контрольных работ | |||||||||||
| Работа 1 | Работа 2 | |||||||||||
Таблица 4
| Номер варианта | Номера задач для контрольных работ | |||||||||||
| Работа 1 | Работа 2 | |||||||||||
Таблица 5
| Номер вари- анта | Номера задач для контрольных работ | ||||||||||||||
| Работа 1 | Работа 2 | Работа 3 | |||||||||||||
|
|
|
Таблица 6
| Номер вари- анта | Номера задач для контрольных работ | ||||||||||||||
| Работа 1 | Работа 2 | Работа 3 | |||||||||||||
Таблица 7
| Номер вари- анта | Номера задач для контрольных работ | |||||||||||||||
| Работа 1 (алгебра и геометрия) | Работа 2 (математический анализ) | Работа 3 (математический анализ) | ||||||||||||||
Таблица 8
| Номер вари- анта | Номера задач для контрольных работ | |||||||||||||||
| Работа 1 (алгебра и геометрия) | Работа 2 (математический анализ) | Работа 3 (математический анализ) | ||||||||||||||
ЗАДАНИЯ КОНТРОЛЬНОЙ РАБОТЫ
|
|
|
В задачах 1—20 даны вершины треугольника AВС. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС в общем виде и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты СD и ее длину; 5) уравнение окружности, для которой высота СD есть диаметр:
| А(-5; 0), В(7; 9), С(5; -5) | А(-5; 2), В(7; -7), С(5; 7) | ||
| А(-7; 2), В(5; 11), С(3; -3) | А(-7; 5), В(5; -4), С(3; 10) | ||
| А(-5; -3), В(7; 6), С(5; -8) | А(-7; 1), В(5; -8), С(3; 6) | ||
| А(-6; -2), В(6; 7), С(4; -7) | А(0; 3), В(12; -6), С(10; 8) | ||
| А(-8; -4), В(4; 5), С(2; -9) | А(-8; 4), В(4; -5), С(2; 9) | ||
| А(0; -1), В(12; 8), С(10; -6) | А(-2; 2), В(10; -7), С(8; 7) | ||
| А(-6; 1), В(6; 10), С(4; -4) | А(1; 2), В(13; -7), С(11; 7) | ||
| А(-2; -4), В(10; 5), С(8; -9) | А(-4; 1), В(8; -8), С(6; 6) | ||
| А(-3; 0), В(9; 9), С(7; -5) | А(-7; -1), В(5; -10), С(3; 4) | ||
| А(-9; -2), В(3; 7), С(1; -7) | А(-3; 3), В(9; -6), С(7; 8) |
В задачах 21—30 даны координаты точек А, В, С. Требуется: 1) записать векторы  и
и 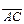 в системе орт и найти модули этих векторов; 2) найти угол в градусах (с точностью до градуса) между векторами
в системе орт и найти модули этих векторов; 2) найти угол в градусах (с точностью до градуса) между векторами  и
и 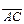 ; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору
; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору  :
:
| А(7; -4; 1), В(12; -3; 1), С(10; 1; 5). | |
| А(0; -3; 3), В(5; -2; 3), С(3; 2; 7). | |
| А(-2; -1; -2), В(3; 0; -2), С(1; 4; 2) | |
| А(-6; 0; 0), В(-1; 1; 0), С(-3; 5; 4) | |
| А(-2; -3; -8), В(3; -2; -8), С(1; 2; -4) | |
| А(1; 0; -1), В(6; 1; -1), С(4; 5; 3) | |
| А(-1; 4; 1), В(4; 5; 1), С(2; 9; 5) | |
| А(3; -6; -3), В(8; -5; -3), С(6; -1; 1) | |
| А(1; 0; 0), В(6; 1; 0), С(4; 5; 4) | |
| А(2; -8; -2), В(7; -7; -2), С(5; -3; 2) |
В задачах 31—40 даны векторы  . Показать, что векторы
. Показать, что векторы  образуют базис трехмерного пространства и найти координаты вектора
образуют базис трехмерного пространства и найти координаты вектора  в этом базисе:
в этом базисе:
 ={2; 1; 3}, ={2; 1; 3},  ={3; -1; 1}, ={3; -1; 1},  ={1; -1; -2}, ={1; -1; -2}, 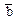 ={7; 0; 7} ={7; 0; 7}
| |
 ={5; 3; 1}, ={5; 3; 1},  ={-2; -1; 2}, ={-2; -1; 2},  ={-2; 1; 4}, ={-2; 1; 4}, 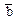 ={3; 0; 1} ={3; 0; 1}
| |
 ={1; 3; 5}, ={1; 3; 5},  ={-2; -1; -1}, ={-2; -1; -1},  ={4; -2; 4}, ={4; -2; 4}, 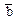 ={-7; 3; -1} ={-7; 3; -1}
| |
 ={3; 1; 6}, ={3; 1; 6},  ={-2; 2; -3}, ={-2; 2; -3},  ={-4; 5; -1}, ={-4; 5; -1}, 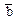 ={3; 0; 1} ={3; 0; 1}
| |
 ={4; 1; 4}, ={4; 1; 4},  ={-2; -1; 1}, ={-2; -1; 1},  ={3; 1; 5}, ={3; 1; 5}, 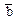 ={-3; -2; 1} ={-3; -2; 1}
| |
 ={1; 2; 5}, ={1; 2; 5},  ={2; -3; 4}, ={2; -3; 4},  ={1; -1; -2}, ={1; -1; -2}, 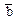 ={3; 0; 1} ={3; 0; 1}
| |
 ={5; 1; 2}, ={5; 1; 2},  ={3; 4; -1}, ={3; 4; -1},  ={-4; 2; 1}, ={-4; 2; 1}, 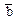 ={-3; 5; 4} ={-3; 5; 4}
| |
 ={2; 1; 5}, ={2; 1; 5},  ={-4; 3; 5}, ={-4; 3; 5},  ={1; -1; -4}, ={1; -1; -4}, 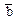 ={4; -1; -3} ={4; -1; -3}
| |
 ={3; 1; 4}, ={3; 1; 4},  ={-4; 2; 3}, ={-4; 2; 3},  ={2; -1; -2}, ={2; -1; -2}, 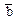 ={7; -1; 0} ={7; -1; 0}
| |
 ={1; 4; 2}, ={1; 4; 2},  ={5; -2; -3}, ={5; -2; -3},  ={-2; -1; 1}, ={-2; -1; 1}, 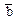 ={-3; 2; 4} ={-3; 2; 4}
|
В задачах 41—50 систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы:

| 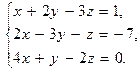
| ||

| 
| ||

| 
| ||
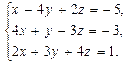
| 
| ||

| 
|
В задачах 51—70 найти указанные пределы (не пользуясь правилом Лопиталя):


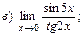



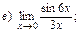

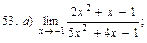


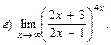

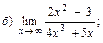
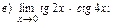








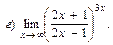












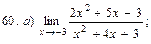
























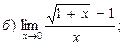

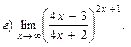
















В задачах 71—90 найти производные функций:
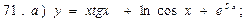









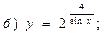

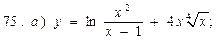

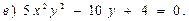
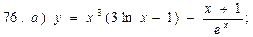








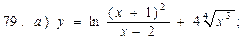


















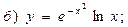


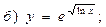


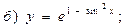









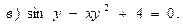
В задачах 91—110 исследовать данные функции методами дифференциального исчисления и построить их графики. Исследование функции рекомендуется проводить по следующей схеме: 1) найти область определения функции; 2) исследовать функцию на непрерывность; 3) определить, является ли данная функция четной, нечетной; 4) найти интервалы монотонности функции и точки ее экстремума; 5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба; 6) найти асимптоты графика функции:

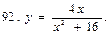
















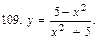

111. Каковы радиус основания R и высота H открытого цилиндрического бака данного объема V, чтобы на его изготовление пошло наименьшее количество листового металла?
112. Сечение тоннеля имеет форму прямоугольника, завершенного сверху полукругом. Периметр сечения 18 м. При каком радиусе полукруга площадь сечения будет наибольшей?
113. Найти стороны прямоугольника наибольшей площади, который можно вписать в эллипс 
114. Найти наибольший объем цилиндра, полная поверхность которого равна S.
115. Найти наибольший объем конуса, образующая которого равна l.
116. Определить размеры открытого бассейна с квадратным дном объемом 32 м3 так, чтобы на облицовку его стен и дна пошло наименьшее количество материала.
117. Сумма двух положительных чисел равна a. Каковы эти числа, если сумма их кубов будет наименьшей?
118. Найти высоту цилиндра наибольшего объема, который можно вписать в шар радиуса R.
119. На параболе y = x2 найти точку, наименее удаленную от прямой
y = 2x - 4.
120. Из всех прямоугольников, вписанных в круг радиуса R, найти тот, который имеет наибольшую площадь.
В задачах 121—125 исследовать на экстремум функцию двух переменных:
121. z = 3x + 3y – x2 – xy – y2 + 6.
122. z = 7x + 8y – x2 – xy – y2 – 10.
123. z = 8x – 4y + x2 – xy + y2 + 15.
124. z = x2 + y2 – 6x – 8y + 12.
125. z = 2x – 8y – x2 – y2 – 9.
В задачах 126—130 найти наименьшее и наибольшее значения функции двух переменных в данной замкнутой области:
126. z = x2 + xy – 6x – 2y + 2 в прямоугольнике 1 £ x £ 3, 1 £ y £ 4.
127. z = x2 + 4xy – y2 – 5 в треугольнике, ограниченном осями Ох и Оу и прямой у = 2 – х.
128. z = x2 + y2 – 10x – 2y + 15 в прямоугольнике 2 £ x £ 6, 0 £ y £ 5.
129. z = x2 – xy + 8х –y + 7 в области, ограниченной параболой
у = –х2 – 4х и осью Ох.
130. z = x2 + 2y2 + 4xy + 2х + 4y + 2 в квадрате 0 £ x £ 2, 0 £ y £ 2.
В задачах 131—150 найти указанные неопределенные интегралы и результаты интегрирования проверить дифференцированием:
| а | б | в | |
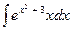
| |||
|
|
|


