Логические действия и операции

 

Эти игры и упражнения предназначены главным образом для старших дошкольников. Они помогут развить у детей уме­ния разбивать множества на классы по совместимым свойст­вам, развить умение производить логические операции «не», «и», «или», умения с помощью этих операций строить правиль­ные высказывания, кодировать и декодировать информацию о свойствах предметов. В результате этих игр и упражнений ре­бенок сможет свободно рассуждать, обосновывать правомер­ность или ошибочность своих действий.

15. «ПОМОГИ ФИГУРАМ ВЫБРАТЬСЯ ИЗ ЛЕСА»

 

Цель. Развитие логического мышления, умения рассуждать.

Материал. Логические фигуры, или блоки, таблицы.

Содержание

Перед детьми таблица 18. На ней изображен лес, в котором заблудились фигурки. Нужно помочь им выбраться из чащи.

Сначала дети устанавливают, для чего на разветвлениях дорог расставлены знаки. Не перечеркнутые знаки разре­шают идти по своей дорожке только таким фигурам, как они сами; перечеркнутые знаки — всем не таким, как они, фигурам. Затем дети разбирают фигуры (блоки) и по очереди выводят их из леса. При этом рассуждают вслух, на какую дорожку каждый раз надо свернуть.

В дальнейших играх используются таблицы 19—21. Дети помогают выбраться из леса фигурам или блокам (табл. 19, 20) или же только блокам (табл. 21).

Для поддержания интереса взрослый ставит перед детьми разнообразные игровые задачи, наделяет фигуры и блоки раз­личными образами. Например, каждая фигура — Дюймовоч­ка (нужно помочь ей выбраться из мышиной норы) или блоки-корабли (надо вывести их из бушующего моря) и т. п.

16. «ЗАГАДКИ БЕЗ СЛОВ»

 

Цель. Развитие умений расшифровывать (декодировать) информацию о наличии или отсутствии определенных свойств у предметов по их знаково-символическим обозначениям.

Материал. Логические блоки, карточки с обозначением свойств.

Содержание

I

Взрослый предлагает детям отгадать необычные загадки: «Это загадки без слов. Я буду показывать карточки со знаками. Знаки подсказывают, какие фигуры загаданы. А вы отгадайте эти фигуры».

Взрослый показывает карточку, например «маленький». Дети ищут соответствующий блок, найдя, оставляют его себе. Тот, кто допускает ошибку, остается без блока. Таким образом предъявляются по одной различные карточки-свойства:

 С целью поддержания интереса у детей взрослый ставит перед детьми разные игровые задачи (собрать для белочки съедобные грибы, найти любимое печенье Винни-Пуха, помочь спрятаться мышатам от проказника кота и т.д.).

Сначала взрослый загадывает блоки, потом загадывают дети. Право загадывать получает тот, кто первым находит блок-отгадку. Выигрывает тот из детей, у кого больше блоков-отгадок. Взрослый поощряет инициативность и самостоятель­ность детей, предлагает новые игровые задачи.

17. «ГДЕ СПРЯТАЛСЯ ДЖЕРРИ?»

 

Цель. Развитие логического мышления, умения коди­ровать информацию о свойствах предметов с помощью знаков-символов и декодировать ее.

Материал. Логические блоки, карточки с обозначением свойств, мышонок Джерри (маленькая плоская фигурка).

Содержание

Перед детьми выкладывают 10—12 блоков. Дети отворачива­ются. Ведущий под одним из блоков прячет мышонка. Дети по­ворачиваются обратно. Ведущий показывает карточку, на кото­рой обозначено свойство того блока, под которым спрятался Джерри. Дети по очереди ищут. Тот, кто находит мышонка, ста­новится ведущим. Он снова прячет фигурку и с помощью кар­точки показывает, под каким блоком находится мышонок.

 

Взрослый побуждает детей обозначать свойство блоков карточками с перечеркнутыми знаками-символами (так сложнее найти мышонка). Для того, чтобы с их помощью обозначить точно цвет блока, нужны две карточки:

 

При повторении игры меняется состав блоков, посте­пенно увеличивается их количество.

Взрослый каждый раз поощряет использование детьми карточек с перечеркнутыми знаками, самостоятельный переход к обозначению новой комбинации свойств.

II

Количество блоков 12—18.

Ведущий с помощью карточек обозначает два свойства того блока, под которым спрятан мышонок. Если ведущий обозначает свойства перечеркнутыми знаками, то сделать это должен как можно точнее. Для этого ему может по­надобиться в некоторых случаях 3, 4 и более карточек.

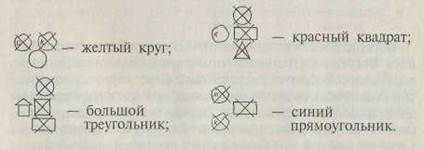Карточки на каждое свойство он выкладывает в отдель­ные ряды или столбики. Например:

При повторении игры частично или полностью меняется состав блоков, постепенно увеличивается их количество. Взрослый каждый раз поощряет стремление детей использо­вать карточки с перечеркнутыми знаками.

III

Количество блоков постепенно увеличивается до 24. Ведущий каждый раз указывает с помощью карточек три свойства того блока, под которым спрятан мышонок Джерри. Свойства блока он обозначает перечеркнутыми и неперечеркнутыми знаками:

Постоянно поощряется стремление детей обозначить перечеркнутыми знаками как можно большее количество свойств блока.

18. «УГАДАЙ ФИГУРУ»

 

Цель. Развитие логического мышления, умений коди­ровать и декодировать информацию о свойствах.

Материал. Логические фигуры и два набора карточек-свойств с перечеркнутыми знаками на каждую пару детей.

Содержание

Дети разбиваются на пары. Каждый выбирает себе одну фигуру так, чтобы не видел партнер. Игроки договарива­ются, какое свойство фигуры будут загадывать (цвет, форму или размер). Затем карточками обозначают загадываемое свойство своей фигуры. Каждый должен угадать, какая фигура у партнера, правильно назвать ее свойство.

За неверный ответ игрок получает в качестве штрафной ту фигуру, свойство которой он не отгадал. Выигрывает тот, у кого окажется меньше штрафных фигур.

Сначала в играх загадывается только одно какое-то свойство фигуры, затем два (например, размер и цвет, размер и форма или цвет и форма).

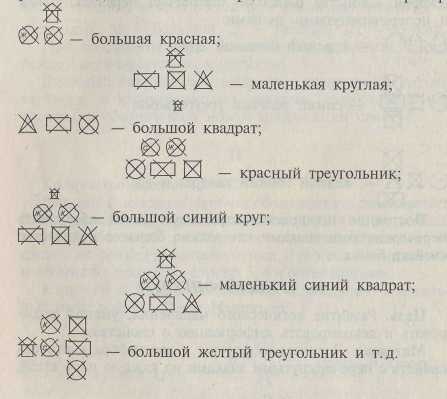
Карточки, обозначающие каждое из двух (трех) свойств, иг­роки выкладывают в отдельные ряды или столбики. Например:

19. «СОКРАТИ СЛОВО»

 

Цель. Развитие логического мышления, умения строго выполнять правила при выполнении действий, внимания.

Материал. Логические блоки (фигуры), таблица 22.

Содержание

Перед детьми 7—9 блоков (круги и квадраты). Блоки выложены в ряд в произвольном порядке — это слово, которое нужно сократить по правилам. Правила записаны на таблице (табл. 22, о). Дети с помощью взрослого выясняют, что означает каждое правило.

Правило 1. Если в слове кружок стоит слева от квадрата, то их нужно поменять ме-стами; применять это правило столько раз, сколько возможно; затем перейти к правилу 2.

Правило 2. Если в слове рядом два кружочка, то их надо убрать; применять правило столько раз, сколько возможно; затем перейти к правилу 3.

Правило 3. Если в слове рядом два квадрата, то их надо убрать; применять правило столько раз, сколько возможно.

Затем дети сокращают слово из квадратов и кругов по этим правилам в направлении слева направо. Начинают сокращать слово всегда с правила 1. В конце выясняют, что же осталось от длинного слова.

С целью повышения интереса детей к упражнению взрослый предлагает детям увлекательные сюжетные си­туации, игровые задачи. Например, рассказывают такую историю: «Узнал Чебурашка, что у Крокодила Гены день рождения, и решил отправить ему поздравительную теле­грамму. Отправился он на почту, взял бланк и написал на нем одно слово «Поздравляю». Вместо букв в этом слове круги и квадраты. Но беда в том, что у Чебурашки не хватило денег, чтобы заплатить за такую длинную телеграмму. Тут пришел на помощь телеграфист. Он пред­ложил Чебурашке сократить слово и дал таблицу, где записано, как нужно это делать».

Упражнение повторяют с новыми словами. Их состав­ляют сами дети. Количество блоков в «словах» постепенно увеличивается. Взрослый всячески стимулирует и поощряет стремление детей предвидеть возможные варианты конеч­ного слова. Для этого как можно чаще предлагает детям угадать, что останется от длинного слова после того, как его сократят. Предположения детей проверяются через практическое преобразование «слова». В дальнейших уп­ражнениях используется таблица 22, б, в. Взрослый пред­лагает детям и самим придумать правила сокращения слов.

20. «ПОСТРОЙ ДОМ»

Цель. Развитие логического мышления, внимания.

Материал. Набор логических фигур в мешочке, 4 кар­точки-домика (см. табл. 23, а), прямоугольники по размеру клеток на карточке (40 штук).

Содержание

В игре принимают участие пять человек: ведущий и строители. У ведущего мешочек с фигурами. У каждого строителя карточка-домик и прямоугольники-«кирпичи». Задача строителей — построить свой дом.

Ведущий по очереди вынимает из мешочка фигуры, называет их форму. Тот, кто находит соответствующее обозначение на карточке, закрывает его прямоугольником-«кирпичиком». Тот, кто первым правильно закроет все знаки на своей карточке (построит свой дом), становится ведущим.

Можно предложить детям варианты карточек, которые потребуют ориентировки на другие свойства (цвет, размер).

II

Используются карточки, которые требуют выделения двух свойств (см. табл. 23, б).

Ведущий, вынимая фигуры из мешочка, называет их цвет и форму. Целесообразно сделать и такие варианты карточек, играя с которыми детям необходимо ориенти­роваться на другие свойства (цвет и размер или форму и размер).

 

III

Используются карточки, которые требуют ориентировки на три свойства (см. табл. 23, в).

Ведущий, вынимая фигуры из мешочка, называет цвет, форму и размер каждой.

21. «РАЗДЕЛИ БЛОКИ-1»

Цель. Развитие умений разбивать множество по одному свойству на два подмножества, производить логическую операцию «не».

Материал. Логические блоки, две игрушки (Буратино, Незнайка).

Содержание

На полу или на столе на расстоянии метра друг от друга расположены игрушки — Буратино и Незнайка. Они соб­рались строить для себя дома из блоков, но поссорились из-за того, что не могут разделить блоки между собой. Взрослый предлагает детям помирить Буратино и Незнайку и помочь им разделить блоки так, чтобы у Незнайки ока­зались все красные.

После выполнения задания дети рассказывают, какие блоки у Незнайки (все красные) и какие у Буратино (все не красные).

Если дети при характеристике блоков Буратино начи­нают называть несколько свойств (желтые и синие), взрос­лый говорит, что нужно ответить одним словом. Если же и погле этого дети отвечают неверно («другие», «не такие» и т.д.), он еще раз обращает их внимание на блоки Незнайки («все красные»); спрашивает, есть ли хотя бы один красный блок у Буратино, и здесь же предлагает назвать, какие все блоки у Буратино в отличие от тех, которые у Незнайки. Если дети и в этом случае не находят нужную форму ответа, подсказывает ее.

При повторении упражнения меняется свойство, по которому дети разбивают блоки: разделить блоки так, чтобы у Буратино оказались все треугольные, или так, чтобы у Незнайки были все желтые, или же так, чтобы к Не­знайке попали все прямоугольные, и т.д.

Сначала правила разделения блоков предлагает взрос­лый, а затем — дети.

Упражнение можно организовывать с использованием обруча.

Взрослый наделяет обручи и блоки образами, предлагает различные сюжеты, например такой.

Обруч — ваза, блоки — цветы. По утрам эльфы приносят Дюймовочке цветы; одни из них ставят в вазу, остальные раскладывают вокруг.

Затем взрослый предлагает детям решить, какие цветы эльфы хотят поставить в вазу, и соответственно разложить блоки.

Обруч и блоки могут наделяться разными образами (об­руч — пруд, блоки — утята; обруч — домик, блоки — его жильцы; обруч — планета, блоки — ее обитатели и др.).

22. «РАЗДЕЛИ БЛОКИ-2»

Цель. Развитие умений разбивать множество по двум совместимым свойствам, производить логические операции «не», «и», «или».

Материал. Логические блоки, две игрушки — Винни-Пух и Пятачок.

Содержание

Перед детьми Винни-Пух и Пятачок. Они в гостях у умного Кролика. Кролик предложил им конфеты (конфеты — блоки), но сказал, что они смогут взять их лишь тогда, когда разделят между собой так, чтобы у Винни-Пуха оказались все желтые, а у Пятачка — все прямоугольные.

Взрослый предлагает детям помочь Винни-Пуху и Пя­тачку решить эту задачу. Сначала он уточняет, запомнили ли дети условие задачи (чтобы не забыли его, можно рядом с игрушками поместить карточки с обозначением указан­ных свойств). Затем помогает определить, куда класть кон­феты, которые подходят и Винни-Пуху и Пятачку (в коробку, расположенную между ними), а также конфеты, ко­торые никому не подходят (например, в ведерко, стоящее в стороне от игрушек).

Дети решают задачу. Если решение неверное (место для общих блоков — коробка — остается пустым), взрослый помо­гает детям самим найти и исправить ошибки. Для этого сначала предлагает проверить, все ли желтые блоки попали к Винни-Пуху, потом — все ли прямоугольные у Пятачка. Дети быстро находят «ошибочные» блоки и начинают перекладывать их от Винни-Пуха к Пятачку и обратно. Однако после нескольких перемещений они приходят к выводу, что и первое и второе решения неверны, и сами делают заключение, что если блок одновременно и прямоугольный и желтый, то он подходит и Винни-Пуху и Пятачку, а его место — в коробке.

После практического решения задачи дети называют, какие конфеты у Винни-Пуха (желтые не прямоугольные), у Пятачка (прямоугольные не желтые), какие ни к кому не попали (не желтые не прямоугольные) и какие оказались общими (желтые прямоугольные).

Если дети указывают в ответах одно из двух заданных свойств, взрослый обращает их внимание на блоки, лежащие в другом месте, которые имеют такое же свойство, просит на­звать их так, чтобы нельзя было спутать ни с какими другими.

С целью развития умения производить логические опе­рации «не», «и», «или» детям предлагается рассказать, каким должен быть блок, чтобы попасть сразу и к Винни-Пуху и к Пятачку (желтым прямоугольным); к одному из них (желтым или прямоугольным); ни к одному из них (не желтым и не прямоугольным).

Если в первых упражнениях дети не смогут дать ответ на эти вопросы, не пытайтесь ответить за них. Они сами сделают это в следующих упражнениях.

Упражнение повторяется. Сначала правила разбиения бло­ков называет взрослый, затем — сами дети. При каждом повтор­ном упражнении меняются свойства — основания разбиения блоков. Например, разделить конфеты так, чтобы у Винни-Пуха оказались все круглые, у Пятачка — все желтые, или у Винни-Пуха — все треугольные, у Пятачка — все синие, или у Винни-Пуха — все синие, у Пятачка — все квадратные и т. д.

В упражнение можно ввести дополнительное правило: если кто-то заметит ошибку, говорит «стоп» и исправляет ее. Это значительно повысит внимание детей, будет спо­собствовать развитию взаимоконтроля.

В ходе практического решения задачи, с целью раз­вития доказательности мышления, взрослый просит детей объяснить, почему они положили свои блоки именно на это место.

Можно предложить детям задачи и с такими условиями: разделить блоки так, чтобы у Винни-Пуха оказались все красные, у Пятачка — все синие, или у Винни-Пуха — все квадратные, у Пятачка — все круглые, или у Винни-Пуха — все большие, у Пятачка — все маленькие.

При практическом решении таких задач место для общих блоков оказывается пустым. Почему так получается, пусть доказывают сами дети.

Повторяя упражнение, взрослый меняет игрушки, игровые задачи и действия, наделяет блоки другими образами.

Дальнейшие упражнения можно проводить как «игры с двумя обручами».

На полу два разноцветных пересекающихся обруча:

 

Сначала дети выясняют, сколько получилось мест (четыре); прыгают на любое из них и говорят, где оно находится: 1-е — внутри обоих обручей, 2-е — внутри красного, но вне синего, 3-е — внутри синего, но вне красного, 4-е — вне обоих обручей.

Затем взрослый наделяет обручи и блоки образами и предлагает игровые задачи. Правила разбиения блоков формулируют сами дети. Например, обручи — цветочные клумбы, блоки — цветы. Клумбы нужно засадить цветами. А как, предлагают дети.

Дети раскладывают блоки, проверяют, все ли блоки на своих местах, и называют эти места.

23. «РАЗДЕЛИ БЛОКИ-3»

Цель. Развитие умений разбивать множества по трем совместимым свойствам, производить логические операции «не», «и», «или», доказательности мышления.

Материал. Логические блоки, три игрушки (волк, заяц, лиса).

Содержание

Перед детьми по кругу расставлены игрушки. Нужно по­мочь им поделить блоки для строительства своих домиков.

Сначала взрослый помогает детям обозначить места для блоков, которые подходят всем трем игрушкам (1), волку и зайцу (2), зайцу и лисе (3), лисе и волку (4); которые никому не подходят (5).

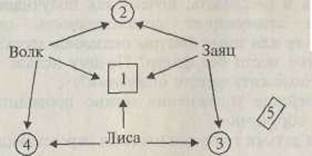Затем предлагает разделить фигуры так, чтобы у волка оказались все круглые, у зайца — все большие, у лисы — все синие, Чтобы дети легче запомнили правило, рядом с игрушками можно положить карточки-свойства.

После практического решения задачи дети называют, какие фигуры оказались общими для всех игрушек (круг­лые большие синие); какие фигуры оказались только у волка (круглые маленькие не синие), только у зайца (большие не круглые не синие), только у лисы (синие маленькие не круглые); какие фигуры общие для волка и зайца (круглые большие не синие), для волка и лисы (круглые синие маленькие), для зайца и лисы (большие синие не круглые); какие фигуры никому не подошли (маленькие не круглые не синие).

Если ребенок, характеризуя группу, называет только два из трех свойств, взрослый обращает его внимание на другие группы блоков, которые имеют указанные свойства; затем просит его еще раз назвать группу, но так, чтобы ее нельзя было спутать ни с какой другой.

При повторении упражнения правило разбиения блоков называют дети. Каждый раз указывается другое сочетание свойств — оснований разбиения блоков.

Например, разделить фигуры так, чтобы у волка оказа­лись все тонкие, у зайца — все треугольные, у лисы — все маленькие, или у волка — все большие, у зайца — все синие, у лисы — все толстые; у волка — все желтые, у лисы — все красные, у зайца — все квадратные и т. д.

Если в результате раскладывания блоков некоторые мес­та (коробки) окажутся пустыми, взрослый побуждает детей выяснить и рассказать, почему так получилось, при этом всячески стимулирует доказательность размышления. (Почему те или иные фигуры оказались здесь? Почему это или другое место без фигур? Почему нельзя те или иные фигуры положить вместе с другими?)

Дальнейшие упражнения можно проводить как «игры с тремя обручами».

Перед детьми три разноцветных пересекающихся обруча:

Сначала взрослый предлагает детям поставить игрушку или прыгнуть на любое из мест в обручах и назвать, где оно находится: 1-е — внутри всех трех обручей, 2-е — внутри желтого и красного, но вне синего обруча, 3-е — внутри красного и синего, но вне желтого обуча, 4-е — внутри желтого и синего, но вне красного обруча, 5-е — внутри желтого, но вне красного и синего обруча, 6-е — внутри красного, но вне желтого и синего обруча, 7-е — внутри синего, но вне желтого и красного, 8-е — вне всех обручей.

Затем дети решают различные игровые задачи, пред­ложенные взрослым: засаживают цветами палисадник, раскладывают пирожные на праздничном столе, состав­ляют мозаику и проч. Правила разбиения блоков они предлагают сами. Например, разложить пирожные на блюда так, чтобы на красном блюде оказались все красные пирожные, на синем — все треугольные, на желтом — все толстые пирожные, или составить мозаику так, чтобы в красном окошке были все круглые стеклышки, в синем — все большие, в желтом — все желтые и т. д.

 

 

123	Поделиться:

Воспользуйтесь поиском по сайту: