Реализация на основе записей (record)

Программная реализация формальных средств анализа и моделирования интегрированных систем ЛА

Для моделирования и анализа процессов функционирования интегрированных систем ЛА с использованием вычислительной техники необходимо программно-математическое обеспечение (ПМО), реализующее описанные в настоящем пособии формальные средства, к которым в первую очередь относятся элементарные процедуры векторной, матричной и кватернионной алгебр, а также различные численные методы (такие как обращение матриц или решение проблемы собственных значений). Такое ПМО удобно представить в виде модуля библиотеки программных средств, предназначенных для решения широкого круга задач компьютерного моделирования процессов функционирования интегрированных систем. Для реализации подобной библиотеки можно использовать различные языки программирования, конкретный выбор может определяться, например, базовой программной платформой, на которой будет функционировать ПМО, специфическими возможностями конкретного языка, предпочтениями разработчика или их коллектива. Некоторые языки программирования и среды моделирования имеют стандартные средства поддержки векторной и матричной алгебры (как, например, Python или MATLAB), но реализация кватернионной алгебры в этих средствах, как правило, отсутствует. Решение же задач моделирования кинематики и динамики ЛА и его систем при современном подходе требует наличие таких возможностей, что вызывает необходимость самостоятельной разработки ПМО, ими обладающего.

В данном пособии рассматриваются различные варианты архитектуры модуля ПМО, реализующего векторные, матричные и кватернионные операции с использованием языков программирования высокого уровня Delphi и С++. Оба эти языка являются объектно-ориентированными, т.е. предоставляют все возможности для гибкой разработки и повторного использования надёжного кода без избыточности. Для них существуют развитые среды разработки (например, Microsoft Visual Studio или QtCreator для С++, Embarcadero RAD Studio для Delphi и С++), и они широко применяются для создания различного ПМО. По сравнению с интерпретируемыми языками, к которым относятся Python и m-язык в среде моделирования MATLAB или Maple, Delphi и С++, являясь компилируемыми, имеют преимущество в быстродействии кода, написанного с их помощью (что становится особенно заметно при организации объёмных вычислений). Нужно отметить, что большинство интерпретируемых языков позволяют автоматически получать на их основе бинарные исполняемые файлы, но создаваемый таким образом машинный код, как правило, оказывается оптимизирован по быстродействию не лучшим образом или не оптимизирован совсем.

По сравнению с упомянутыми средами разработки, обеспечивающими удобное создание графического интерфейса пользователя, который зачастую является неотъемлемой частью сложных моделирующих комплексов, возможности MATLAB весьма ограничены, а в Python для этой цели требуются внешние библиотеки и средства разработки. Кроме того, Delphi продолжает оставаться одним из основных языков для обучения программированию, являясь при этом полноценным инструментом, пригодным для решения вычислительных задач. Что касается С++, то на сегодняшний день это самый распространённый язык программирования, компиляторы которого реализованы на большинстве существующих платформ, в том числе и для бортовых систем.

В целях демонстрации различных возможностей рассматриваемых языков программирования, которые могут использоваться при реализации и других компонентов моделирующих комплексов, для каждого из этих языков приводится по два примера исходного кода с комментариями и пояснениями. Каждый вариант реализации имеет свои преимущества и недостатки, поэтому выбор конкретного варианта для практического применения должен определяться с их учётом.

Примеры реализации ПМО на Delphi

Реализация модуля процедур векторной, матричной и кватернионной алгебры на Delphi может быть выполнена различными способами. Для непосредственного хранения данных (элементов векторов, матриц) удобно использовать динамические массивы, являющиеся частью языка и позволяющие не заботиться о механизмах выделения и удаления памяти. Объявление типов одномерного и двумерного динамических массивов действительных чисел с повышенной точностью (типа Extended) может иметь вид:

Type

T1DArray: array of Extended;

T2DArray: array of array of Extended;

Выделение памяти для экземпляров таких типов осуществляется вызовом системной процедуры с переменным числом параметров System.SetLength(arg, 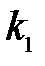, , …, ), где arg – переменная типа «динамический массив» размерности N, а – нужное количество элементов в каждом измерении этого массива. Для освобождения памяти достаточно выполнить присвоение arg:= nil или явно указать нулевые размеры в каждом измерении динамического массива: System.SetLength(arg, 0, 0, …, 0). Для получения информации о количестве элементов динамического массива следует использовать функцию System.Length(arg), при этом допустимы обращения ко второму и последующим измерениям массива: System.Length(arg[ , , …, ]), где 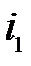– номер интересующего элемента в первом измерении, – во втором и т.д. до измерения (N -1).

Динамический массив в Delphi – это ссылочный тип, т.е. при выполнении прямого присваивания в новую переменную будет скопировано не содержимое массива, а только ссылка на старое содержимое. Чтобы при присваивании создать копию исходного массива, можно воспользоваться функцией Copy:

B:= Copy(A);

где A – переменная, ссылающаяся на существующий в памяти динамический массив, B – переменная того же типа, которая после выполнения указанной операции будет ссылаться на копию исходного массива. Вторым вариантом является копирование в новую переменную ссылки на исходный массив и последующий вызов функции изменения размера массива для этой новой переменной:

B:= A;

System.SetLength(B, System.Length(B));

В результате выполнения этих операций встроенный в Delphi механизм управления памятью разделит ссылки A и B, создав для B копию исходного динамического массива.

Следует отметить, что при организации математических вычислений на Delphi для работы с действительными числами рекомендуется всегда использовать тип Extended, обеспечивающий повышенную точность вычислений на платформе x86 за счёт представления в памяти в виде 10 байт (80 бит), в отличие от типов Float или Double, число байт для которых меньше (4 и 8 соответственно). На платформе x64 из соображений совместимости тип Extended является синонимом для типа Double, т.е. занимает 8 байт вместо 10. При этом на платформе x86 разрядность 80 бит для арифметических операций поддерживается на аппаратном уровне (процессором), т.е. является естественной для представления действительных чисел.

Объединение описанного способа хранения данных с реализацией вычислительных операций над векторами, матрицами и кватернионами удобно сделать с использованием объектно-ориентированного подхода. Ниже рассматриваются два возможных варианта такой реализации – на основе записей (record) и классов (class). Каждый из этих вариантов имеет свои преимущества и недостатки, которые следует учитывать при выборе одного из них для практического использования.

Реализация на основе записей (record)

Тип record (запись) в современных версиях Delphi может использоваться не только для традиционного представления структур данных в виде простой совокупности полей, но также позволяет объявлять более сложные типы, во многом подобные классам. В дополнение к полям, записи могут содержать свойства, методы (включая конструкторы) и объявления вложенных типов. Также в записях допускаются так называемые классовые поля, свойства и методы (объявляемые с ключевым словом class).

Но записи имеют также и ряд важных отличий от классов:

· Записи не поддерживают наследование.

· Если объекты записи не объявлены глобальными или для их создания и удаления не используются явные вызовы функций New и Dispose, то память для таких объектов выделяется на стеке, они копируются при присваивании и передаются в функции и обратно по значению. Классы же относятся к ссылочным типам, их объекты не копируются при присваивании, передаются по ссылке, а память для них выделяется в «куче» после явного вызова конструктора.

· Записи позволяют перегружать операторы, а классы – нет.

· Записи создаются автоматически с помощью конструктора без аргументов, который всегда неявно присутствует в записи. Поэтому любые конструкторы, которые необходимо добавить к записи, должны иметь хотя бы один параметр.

· Записи не могут иметь деструкторов.

· Записи не могут иметь виртуальных методов (объявляемых со спецификаторами virtual, dynamic или message).

· Записи не могут реализовывать интерфейсы.

С точки зрения организации модуля вычислительных методов векторной, матричной и кватернионной алгебр, важной особенностью записей является возможность перегрузки арифметических операторов, что делает весьма удобным последующее использование объектов и методов данного модуля. Также важным обстоятельством является то, что записи автоматически размещаются и удаляются из памяти, т.к. не относятся к ссылочным типам, что снимает проблему контроля используемой памяти.

К существенным недостаткам использования записей в рамках обсуждаемого модуля можно отнести ограничения принципов ООП – отсутствие возможности наследования и применения виртуальных методов. При необходимости расширения функционала модуля или замены реализации какого-либо метода на альтернативную потребуется переработка исходного кода самого модуля, что не всегда может быть возможно или допустимо при совместном использовании кода в составе различных проектов.

Ниже представлен пример объявления структур типа вектор (TVector), матрица (TMatrix) и кватернион (TQuaternion) в рамках описанного подхода (содержимое секции Interface модуля с комментариями). Диаграмма классов не приводится в связи с её тривиальностью.

Листинг 1.

Interface

// Объявления новых типов

Type

// Опережающая декларация ссылочного типа на структуру типа TQuaternion

PQuaternion = ^TQuaternion;

// Структура типа вектор

TVector = record

Private

// Массив элементов

data: array of Extended;

// Функция получения значения элемента

function GetItem(i: Integer): Extended;

// Процедура установки значения элемента

procedure SetItem(i: Integer; value: Extended);

// Функция получения размера вектора

function GetSize: Integer;

// Функция получения индекса последнего элемента

function GetHigh: Integer;

Public

// Функция создания копии объекта

function Clone: TVector;

// Функция изменения размера вектора

procedure Resize(n: Integer);

// Оператор неявного преобразования обычного массива в TVector

class operator Implicit(a: array of Extended): TVector;

// Оператор унарный минус

class operator Negative(a: TVector): TVector;

// Оператор сложения векторов

class operator Add(a, b: TVector): TVector;

// Оператор вычитания векторов

class operator Subtract(a, b: TVector): TVector;

// Оператор умножения вектора на число

class operator Multiply(a: TVector; b: Extended): TVector; overload;

// Оператор умножения числа на вектор

class operator Multiply(a: Extended; b: TVector): TVector; overload;

// Оператор скалярного произведения векторов

class operator Multiply(a, b: TVector): Extended; overload;

// Функция векторного произведения векторов

function Cross(a: TVector): TVector;

// Функция получения модуля вектора

function Length: Extended;

// Поворот векора вокруг заданной оси на заданный угол при помощи формулы Родрига

function rotateByRodrigFormula(phi: Extended; axis: TVector): TVector;

// Поворот векора вокруг заданной оси на заданный угол при помощи кватерниона

function rotate(phi: Extended; axis: TVector): TVector;

// Поворот векора вокруг заданной оси на заданный угол при помощи кватерниона

function rotateByQuaternion(Q: PQuaternion): TVector;

// Процедура нормирования вектора

procedure Norm;

// Свойство для чтения и изменения размера вектора

property Size: Integer read GetSize write Resize;

// Свойство для чтения индекса последнего элемента

property High: Integer read GetHigh;

// Свойство для доступа к элементам вектора

property Item[i: Integer]: Extended read GetItem write SetItem; default;

end;

// Структура типа матрица

TMatrix = record

Private

// Двумерный массив элементов

data: array of array of Extended;

// Функция получения значения элемента

function GetItem(i,j: Integer): Extended;

// Процедура установки значение элемента

procedure SetItem(i,j: Integer; value: Extended);

// Функция получения кол-ва строк

function GetRowCount: Integer;

// Функция получения кол-ва столбцов

function GetColCount: Integer;

// Функция получения индекса последней строки

function GetRowHigh: Integer;

// Функция получения индекса последнего столбца

function GetColHigh: Integer;

Public

// Функция создания копии объекта

function Clone: TMatrix;

// Функция изменения размерности

procedure Resize(n, m: Integer);

// Оператор унарный минус

class operator Negative(a: TMatrix): TMatrix;

// Оператор сложения матриц

class operator Add(a, b: TMatrix): TMatrix;

// Оператор вычитания матриц

class operator Subtract(a, b: TMatrix): TMatrix;

// Оператор умножения матрицы на матрицу

class operator Multiply(a, b: TMatrix): TMatrix; overload;

// Оператор умножения матрицы на число

class operator Multiply(a: TMatrix; b: Extended): TMatrix; overload;

// Оператор умножения числа на матрицу

class operator Multiply(a: Extended; b: TMatrix): TMatrix; overload;

// Оператор умножения матрицы на вектор

class operator Multiply(a: TMatrix; b: TVector): TVector; overload;

// Оператор умножения вектора на матрицу

class operator Multiply(a: TVector; b: TMatrix): TVector; overload;

// Функция вычисления определителя

function Det: Extended;

// Функция обращения матрицы

function Inv: TMatrix;

// Функция транспонирования матрицы

function T: TMatrix;

// Порождающая функция для формирования единичной матрицы

class function E(n: Integer): TMatrix; static;

// Процедура перестановки строк

procedure SwapRows(i, j: Integer);

// Свойство для достуа к элементам матрицы

property Item[i,j: Integer]: Extended read GetItem write SetItem; default;

// Свойство для получения строки матрицы, как вектора

property Row[i: Integer]: TVector read GetRow;

// Свойство для чтения количества строк

property RowCount: Integer read GetRowCount;

// Свойство для чтения количества столбцов

property ColCount: Integer read GetColCount;

// Свойство для чтения индекса последней строки

property RowHigh: Integer read GetRowHigh;

// Свойство для чтения индекса последнего столбца

property ColHigh: Integer read GetColHigh;

end;

// Структура типа кватернион

TQuaternion = record

Private

// Скалярная часть кватерниона

q0: extended;

// Скалярная часть кватерниона

Q: TVector;

// Функция получения значения элемента

function GetItem(i: Integer): Extended;

// Функция получения векторной части кватерниона

function GetVect: TVector;

Public

// Функция создания копии объекта

function Clone: TQuaternion;

// Производящая функция для создания кватерниона по его компонентам

class function fromElements(q0, q1, q2, q3: Extended): TQuaternion; static;

// Производящая функция для создания кватерниона по углу и оси поворота

class function fromAngleAndAxis(phi: Extended; e: TVector): TQuaternion; static;

// Производящая функция для создания кватерниона по углам Крылова

class function fromKrylovAngles(yaw, pitch, roll: Extended): TQuaternion; static;

// Оператор унарный минус

class operator Negative(a: TQuaternion): TQuaternion;

// Оператор сложения кватернионов

class operator Add(a, b: TQuaternion): TQuaternion;

// Оператор вычитания кватернионов

class operator Subtract(a, b: TQuaternion): TQuaternion;

// Оператор умножения кватернионов

class operator Multiply(a, b: TQuaternion): TQuaternion; overload;

// Оператор умножения кватерниона на число

class operator Multiply(a: TQuaternion; b: Extended): TQuaternion; overload;

// Оператор умножения числа на кватернион

class operator Multiply(a: Extended; b: TQuaternion): TQuaternion; overload;

// Оператор умножения кватерниона на вектор

class operator Multiply(a: TQuaternion; b: TVector): TQuaternion; overload;

// Оператор умножения вектора на кватернион

class operator Multiply(a: TVector; b: TQuaternion): TQuaternion; overload;

// Функция нормирования кватерниона

function norm: TQuaternion;

// Функция получения сопряженного кватерниона

function conj: TQuaternion;

// Функция обращения кватерниона

function inv: TQuaternion;

// Функция получения матрицы вращения из компонентов кватерниона

function toRotateMatrix: TMatrix;

// Свойство для чтения к элементам кватерниона

property Item[i: Integer]: Extended read GetItem; default;

// Свойство для чтения векторной части кватерниона

property Vect: TVector read GetVect;

// Свойство для чтения скалярной части кватерниона

property Scal: Extended read q0;

end;

Важно отметить метод Clone, который обеспечивает создание в памяти копии объекта, для которого он вызывается. Использование этого метода обязательно при необходимости выполнить прямое присваивание одного объекта другому: А:=B.Clone. Недопустимо использовать конструкцию вида A:=B из-за того, что при таком присваивании область памяти, в которой хранятся данные объекта B, не будет скопирована, а в объект A будет перенесён лишь указатель на неё, хранящийся в поле data.

Ключевое слово default, указанное после деклараций индексированных свойств доступа к элементам вектора, матрицы и кватерниона, позволяет обращаться к этим свойствам неявно – без указания их имени, например: A[i] вместо A.Item[i], где А – экземпляр структуры TVector.

Использование ссылочного типа PQuaternion для аргумента функции rotateByQuaternion структуры TVector вызвано невозможностью применить опережающую декларацию непосредственно к записям (record) в отличие от классов. Между тем, какая-то альтернатива такой декларации необходима, так как структура TQuaternion объявляется позже структуры TVector, аргумент упомянутого метода которой является кватернионом. Выходом и является использование ссылочного типа в опережающей декларации. При обращении к переменной ссылочного типа как к экземпляру соответствующей структуры следует использовать оператор «^» после имени переменной, например: Q^.

Применение перегруженных операторов позволяет впоследствии записывать расчётные соотношения в коде наиболее естественным образом. например: C:= A+B.

В секции Implementation приводится реализация методов перечисленных структур. В рамках данного пособия невозможно детально описать реализацию каждого метода, поэтому ниже представлена реализация только базовых служебных процедур и функций, а также некоторых алгебраических методов (сложения векторов, умножения матриц, умножения кватерниона на другой кватернион и на вектор) для демонстрации рекомендуемого подхода к реализации остальных методов.

Листинг 2.

Implementation

uses SysUtils;

// Функция получения значения элемента

function TVector.GetItem(i: Integer): Extended;

Begin

Result:= data[i];

end;

// Процедура установки значения элемента

procedure TVector.SetItem(i: Integer; value: Extended);

Begin

data[i]:= value;

end;

// Функция создания копии объекта

function TVector.Clone: TVector;

Begin

Result:= self;

Result.Resize(self.Size);

end;

// Функция изменения размера вектора

procedure TVector.Resize(n: Integer);

Begin

SetLength(data, n);

end;

// Функция получения размера вектора

function TVector.GetSize: Integer;

Begin

Result:= System.Length(data);

end;

// Функция получения индекса последнего элемента

function TVector.GetHigh: Integer;

Begin

Result:= System.High(data);

end;

// Оператор неявного преобразования к обычному динамическому массиву

class operator TVector.Implicit(a: array of Extended): TVector;

Var

n, i: Integer;

Begin

n:= System.Length(a);

Result.Resize(n);

for i:= n-1 downto 0 do

Result.data[i]:= a[i];

end;

// Оператор сложения векторов

class operator TVector.Add(a, b: TVector): TVector;

Var

i: Integer;

Begin

{$IFDEF Debug}

if a.Size <> b.Size then

raise Exception.Create('Несовместимые размерности');

{$ENDIF}

Result.Resize(a.Size);

for i:= 0 to a.High do

Result[i]:= a[i] + b[i];

end;

// Поворот вектора вокруг заданной оси на заданный угол при помощи кватерниона

function TVector.rotateByQuaternion(Q: PQuaternion): TVector;

Begin

RESULT:= (Q^ * self * Q.conj).Vect;

end;

// Функция получения значения элемента матрицы

function TMatrix.GetItem(i, j: Integer): Extended;

Begin

Result:= data[i, j];

end;

// Функция установки значение элемента

procedure TMatrix.SetItem(i, j: Integer; value: Extended);

Begin

data[i, j]:= value;

end;

// Функция для получения строки матрицы как вектора

function TMatrix.GetRow(i: Integer): TVector;

Var

n, j: Integer;

Begin

n:= GetColCount;

Result.Resize(n);

for j:= n-1 downto 0 do

Result.data[j]:= data[i, j];

end;

// Функция получения количества строк

function TMatrix.GetRowCount;

Begin

Result:= Length(data);

end;

// Функция получения количества столбцов

function TMatrix.GetColCount;

Begin

if Length(data) > 0 then

Result:= Length(data[0])

Else

Result:= 0;

end;

// Функция получения индекса последней строки

function TMatrix.GetRowHigh: Integer;

Begin

Result:= GetRowCount - 1;

end;

// Функция получения индекса последнего столбца

function TMatrix.GetColHigh: Integer;

Begin

Result:= GetColCount - 1;

end;

// Функция создания копии объекта

function TMatrix.Clone: TMatrix;

Begin

Result:= self;

Result.Resize(self.RowCount, self.ColCount);

end;

// Функция изменения размерности

procedure TMatrix.Resize(n, m: Integer);

Begin

SetLength(data, n, m);

end;

// Оператор умножения матрицы на матрицу

class operator TMatrix.Multiply(a, b: TMatrix): TMatrix;

Var

i, j, k: Integer;

Begin

{$IFDEF Debug}

if (a.ColCount <> b.RowCount) then

raise Exception.Create('Несовместимые размерности');

{$ENDIF}

Result.Resize(a.RowCount, b.ColCount);

for i:= 0 to Result.RowHigh do

for j:= 0 to Result.ColHigh do

Begin

Result[i,j]:= 0;

for k:= 0 to a.ColHigh do

Result[i,j]:= Result[i,j] + a[i,k] * b[k,j];

end;

end;

// Функция получения значения элемента кватерниона

function TQuaternion.GetItem(i: Integer): Extended;

Begin

{$IFDEF Debug}

if (i < 0) or (i > 3) then

raise Exception.Create('Неверный индекс элемента кватерниона');

{$ENDIF}

if i = 0 then

Result:= q0

Else

Result:= Q[i-1];

end;

// Функция получения векторной части кватерниона

function TQuaternion.GetVect: TVector;

Begin

Result:= Q.Clone;

end;

// Функция создания копии объекта

function TQuaternion.Clone: TQuaternion;

Begin

Result.q0:= q0;

// При копировании векторной части используется метод Clone

Result.Q:= Q.Clone;

end;

// Производящая функция для создания кватерниона по его компонентам

class function TQuaternion.fromElements(q0, q1, q2, q3: Extended): TQuaternion;

Begin

Result.q0:= q0;

Result.Q.Resize(3);

Result.Q[0]:= q1;

Result.Q[1]:= q2;

Result.Q[2]:= q3;

end;

// Производящая функция для создания кватерниона по углу и оси поворота

class function TQuaternion.fromAngleAndAxis(phi: Extended; e: TVector): TQuaternion;

Begin

{$IFDEF Debug}

if (e.Size <> 3) then

raise Exception.Create('Неверно задан вектор оси поворота');

{$ENDIF}

Result.q0:= cos(phi/2);

Result.Q:= e.Clone;

Result.Q.norm();

Result.Q:= Result.Q * sin(phi/2);

end;

// Оператор умножения кватернионов

class operator TQuaternion.Multiply(a, b: TQuaternion): TQuaternion;

Begin

Result.q0:= a.q0 * b.q0 – a.Q * b.Q;

Result.Q:= a.Q * b.q0 + b.Q*a.q0 + a.Q.Cross(b.Q);

end;

// Оператор умножения кватерниона на вектор

class operator TQuaternion.Multiply(a: TQuaternion; b: TVector): TQuaternion;

Begin

Result:= a * TQuaternion.fromElements(0, b[0], b[1], b[2]);

end;

Следует обратить внимание на использование директивы условной компиляции {$IFDEF Debug}…{$ENDIF} в реализации методов сложения векторов, умножения матриц и др. Она позволяет, в зависимости от режима компиляции, включить или исключить из программы некоторый код, который помещён между операторами директивы {$IFDEF Debug} и {$ENDIF}. Параметр Debug является системным параметром среды разработки Delphi RAD Studio, который принимает значение TRUE в случае компиляции программы в режиме отладки, и FALSE – в противном случае. В нашем случае такой код может осуществлять контроль размерностей операндов (например, при умножении матриц) и генерирует специальный объект исключения класса Exception с сообщением об ошибке (для этого используется оператор raise). В режиме отладки такой контроль может быть полезен для недопущения обращения к «чужой» области памяти и облегчения поиска ошибок в программе. При возникновении исключительной ситуации работа программы будет прервана, а на экране в диалоговом окне будет отображено соответствующее сообщение. После окончания отладки и компиляции программы в рабочем режиме такой код в подавляющем большинстве случаев становится избыточным – в корректно работающей программе моделирования функционирования интегрированных систем ЛА не должно возникать ситуаций несовпадения размерностей операндов в векторной и матричной алгебре. Использование описанной конструкции в таком случае обеспечивает исключение этого фрагмента кода из программы при компиляции в рабочем режиме, что приведёт к увеличению её быстродействия.

Пример использования объектов, имеющих описанные структуры:

Листинг 3.

Var

// Объявление переменных – экземпляров структур типа матрица, вектор, кватернион

A, B, C: TMatrix;

X, Y, Z: TVector;

L: TQuaternion;

Begin

// Установка размерности матриц А, В и вектора X

A.Resize(3, 3);

B.Resize(3, 3);

X.Resize(3);

// Инициализация элементов матриц и вектора

A[0, 0]:= 1; A[0, 1]:= 2; …

B[0, 0]:= 10; B[0, 1]:= 20; …

X[0]:= 1; X[1]:= 2; X[2]:= 3;

// Инициализация вектора массивом чисел типа Extended

Y:= [5.1, 6.3, 7.2];

// Сложение матриц А и В и присваивание результата матрице С

C:= A + B;

// Умножение матрицы С на вектор X и присваивание результата вектору Z

Z: = C * X;

// Инициализация кватерниона Q с помощью производящей функции по значению угла поворота и вектора оси вращения

Q:= TQuaternion.fromAngleAndAxis(Pi/2, X);

// Умножение числа на вектор

Z:= 2 * X;

// Поворот вектора Z при помощи кватерниона Q и присваивание результата вектору X

X:= Z.rotateByQuaternion(Q);

// Создание копии вектора X и присваивание её вектору Y

Y:= X.Clone;

end;

В данном фрагменте кода продемонстрировано объявление переменных типа вектор, матрица и кватернион, а также использование этих переменных в некоторых расчётах.

1234	Поделиться:

Воспользуйтесь поиском по сайту: