Формулы для вычисления площади треугольника через радиусы.

Площадь треугольника (через радиус описанной окружности; через радиус вписанной окружности). .

26. Вектор. Координаты вектора. Длина вектора.

Определение. Вектор- это направленный отрезок имеющий начало и конец. Обозначается например или .

Пусть А - начало вектора и B - конец вектора

Тогда координатами вектора называются 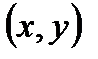, где , ;

Длина вектора .

27. Равные вектора. Коллинеарные вектора. Их свойства.

Два вектора называются равными, если они коллиниарные и имеют одинаковую длину и направление.(равные вектора имеют равные координаты).

Вектора называются коллинеарными, если существует прямая, которой они параллельны.

 

28. Коллинеарные вектора – это вектора, у которых координаты пропорциональны.

Пусть вектор - вектор , тогда

.

29. Координаты середины отрезка.

Если необходимо найти т. С (,середину отрезка АВ,(т.А , т.B ), тогда координата точки С , равна , .

30. Расстояние между точками. 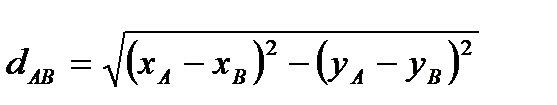(обозначения смотри выше).

31. Алгебраические операции над векторами.

Сумма векторов и называется вектор идущий из начала вектора , в конец вектора , при условии, что вектор приложен к концу вектора . Обозначается + = .

Разность векторов и называется вектор ,который в сумме с вектором дает .

(Построение) Разность векторов и называется вектор идущий из конца вектора к концу вектора , при условии, что вектора и приложены к одной точке.

- =

.

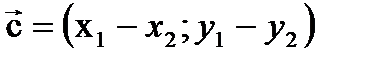Произведение вектора на число - это коллинеарный ему вектор , со направленный с вектором если >0 и направленный противоположно вектору если <0.

32. Разложение вектора по двум неколлинеарным векторам.

Теорема (о разложении вектора). Любой вектор можно разложить, притом единственным образом, по двум данным неколлинеарным векторам и , в виде вектора .

33. Скалярное произведение векторов, его свойства.

Скалярное произведение векторов – называется произведение их длин на косинус угла между ними.

по определению

в координатной форме.

34. Условие перпендикулярности векторов. Два вектора перпендикулярны когда их скалярное произведение равно 0.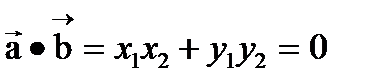

 

35. Нахождение угла между векторами.

 

= .

Часть 2 «Основы стереометрии»

 

1. Расстояние от точки до прямой; до плоскости.

Определение 1. Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.

Определение 2.Расстояние от точки до плоскости – это длина перпендикуляра, опущенного из заданной точки к заданной плоскости.

2. Свойство точки равноудаленной от сторон многоугольника; от вершин многоугольника.

Свойство 1. Если через центр вписанной в многоугольник окружности проведена прямая перпендикулярная плоскости многоугольника, то все точки этой прямой равноудалены от сторон многоугольника.

Свойство 2. Если через центр описанной около многоугольника окружности проведена прямая перпендикулярная плоскости многоугольника, то все точки этой прямой равноудалены от вершин многоугольника.

3. Угол между прямыми в пространстве.

Определение. Углом между прямыми в пространстве будем называть любой из углов, образованных двумя прямыми, проведенными через произвольную точку параллельно данным.

4. Угол между прямой и плоскостью.

Определение. Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость.

5. Угол между плоскостями.

Определение. Двугранный угол между плоскостями равен углу образованному прямыми l₁ и l₂, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.(Величиной угла между плоскостями называется величина меньшего двугранного угла).

6. Признак параллельности прямых.

Теорема. (Признак) Если две прямые в пространстве параллельны третьей прямой, то они параллельны.

7. Признак параллельности прямой и плоскости.

Теорема .(Признак). Если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости.

 

8. Признак параллельности плоскостей.

Теорема (Признак).Если две пересекающиеся прямые одной плоскости cоответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

9. Теорема о двух плоскостях пересеченных третьей.

Теорема. Если две параллельные плоскости пересекаются третьей плоскостью, то прямые образованные этим пересечением параллельны.

10. Признак перпендикулярности плоскостей.

Теорема. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

11. Теорема о трех перпендикулярах.

Теорема. Прямая, лежащая в плоскости и перпендикулярная проекции наклонной к этой плоскости, перпендикулярна и самой наклонной.

12. Теорема о площади ортогональной проекции.

Теорема. Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции.

Часть 3 «Тела вращения. Многогранники»

1. Куб – Правильная четырехугольная призма, каждая грань которого представляет собой квадрат.

Диагональ грани

Диагональ куба

Площадь полной поверхности

Площадь боковой поверхности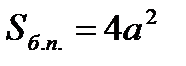

Объем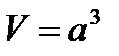

2. Параллелепипед – Четырехугольная призма, каждая грань которого представляет собой параллелограмм.

 

ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕД - это параллелепипед, боковые рёбра которого перпендикулярны основанию.

 

Площадь полной поверхности , где S_о — площадь основания.

Площадь боковой поверхности , где Р_о — периметр основания,

h — высота

Объем .

Прямоугольный параллелепипед (прямая четырехугольная призма каждая грань которой является прямоугольником.

Площадь боковой поверхности S_б=2c(a+b), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда

Площадь полной поверхности S_п=2(ab+bc+ac)

Объём V=abc, где a, b, c — измерения прямоугольного параллелепипеда.

12	Поделиться:

Воспользуйтесь поиском по сайту: