Применение теплоты в сельском хозяйстве

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

ДЛЯ ВЫПОЛНЕНИЯ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ

 

СТУДЕНТАМ ИНЖЕНЕРНЫХ СПЕЦИАЛЬНОСТЕЙ СЕЛЬСКОХОЗЯЙСТВЕННЫХ ВУЗОВ

 

Составитель: Рязанов А.Б.

 

 

Оренбург 2011

1. Теплопроводность через многослойную плоскую стенку

 

Согласно второму закону термодинамики самопроизвольный процесс переноса теплоты в пространстве возникает под действием разности температур и направлен в сторону уменьшения температуры. Закономерности переноса теплоты и количественные характеристики этого процесса являются предметом исследования теории теплообмена (теплопередачи).

Теплота может распространяться в любых веществах и даже через вакуум (пустоту). Идеальных теплоизоляторов не существует. Во всех веществах теплота передается теплопроводностью за счет переноса энергии микрочастицами. За счет взаимодействия друг с другом быстродвижущиеся микрочастицы отдают свою энергию более медленным, перенося таким образом теплоту из зоны с высокой в зону с более низкой температурой. В теории теплообмена, как и в гидромеханике, термином «жидкость» обозначается любая сплошная среда, обладающая свойством текучести. Подразделение на «капельную жидкость» и «газ» используется только в случае, когда агрегатное состояние вещества играет в рассматриваемом процессе существенную роль.

Следует иметь в виду, что одновременно с конвекцией всегда сосуществует и теплопроводность, однако конвективный перенос в жидкостях обычно является определяющим, поскольку он значительно интенсивнее теплопроводности. В твердых монолитных телах перемещение макроскопических объемов относительно друг друга невозможно, поэтому теплота переносится в них только теплопроводностью. Однако при нагреве, сушке зернистых материалов (песка, зерна и т. д.) очень часто искусственно организуют перемешивание. Процесс теплопереноса при этом резко интенсифицируется и физически становится похожим на конвективный теплоперенос в жидкостях. Часто приходится рассчитывать теплообмен между жидкостью и поверхностью твердого тела. Этот процесс получил специальное название конвективная теплоотдача (теплота отдается от жидкости к поверхности или наоборот).

Количество теплоты, передаваемое в единицу времени через произвольную поверхность, в теории теплообмена принято называть мощностью теплового потока или просто тепловым потоком и обозначать буквой Q. Единица ее измерения - Вт.

Тепловой поток через многослойную плоскую стенку рассчитывается по следующему уравнению:

, (1)

где Q – тепловой поток, Вт; t_ст1 и t_ст2 – температуры наружных поверхностей; ⁰С; S – площадь стенки, м²; 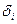- толщина i-го слоя, м; 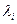- коэффициент теплопроводности материала i-й стенки, .

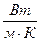Температуры между отдельными слоями стенки находятся из уравнений:

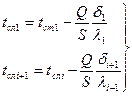(2)

Рисунок 1. Пример графического изображения распределения температуры в многослойной стенке

Задание. Найти тепловой поток через трехслойную плоскую стенку площадью 15 м², а также температуры между отдельными слоями. Изобразить распределение температуры в данной стенке. Исходные данные взять из таблицы 1 согласно варианту.

 

Таблица 1.

Номер варианта	tст1, 0С	tст2, 0С
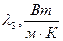
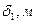
					0,1	0,001	0,2	0,01
					0,2	0,002	0,4	0,02
					0,3	0,003	0,6	0,03
					0,4	0,004	0,8	0,04
					0,5	0,005		0,05
					0,6	0,006	1,2	0,06
					0,7	0,007	1,4	0,07
					0,8	0,008	1,6	0,08
					0,9	0,009	1,8	0,09
						0,01		0,1

 

2. Теплопередача через плоскую стенку

 

Количество теплоты, переданное от одного газа (жидкости) к другому за секунду, разделенных плоской стенкой, находится по выражению

, (3)

где - коэффициент теплоотдачи от горячего теплоносителя с постоянной температурой t₁ к поверхности стенки, учитывающий все воды теплообмена, ; - коэффициент теплоотдачи от второй поверхности стенки к холодному теплоносителю с постоянной температурой t₂, ; S – расчетная площадь поверхности стенки, м²; 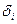- толщина i-го слоя, м; 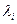- коэффициент теплопроводности материала i-й стенки, 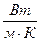. Значения температуры можно брать как в градусах Цельсия, так и в Кельвинах.

Температуры на поверхностях плоской стенки определяются из следующих уравнений:

(4)

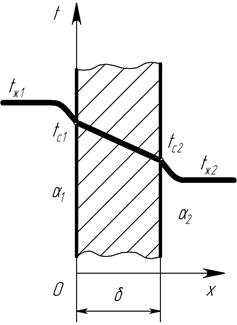
Рисунок 2. Пример графического изображения распределения температуры в однослойной стенке

 

Задание. Найти тепловой поток через однослойную плоскую стенку, а также температуры поверхностей стенки. Изобразить распределение температуры в данной стенке. Исходные данные взять из таблицы 2 согласно варианту.

Таблица 2.

Номер варианта	t1, 0С	t2, 0С		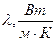			S, м2
				0,001
				0,002
				0,003
				0,004
				0,005
				0,006
				0,007
				0,008
				0,009
				0,01

 

 

Литература

 

1. Цвятков Ф.Ф. Тепломассообмен.- М.Издательский дом МЭИ, 2006.-550с.

2. Драганов Б.Х. и др. Теплотехника и применение теплоты в сельском хозяйстве: Учеб по инж. спец. сел. хоз-ва. М.: Агропромиздат, 1990. – 462 с.

3. Нащокин В. В. Техническая термодинамика и теплопередача: Учебное пособие. – 3-е изд., испр. и доп. М.: Высшая школа, 1980. – 469 с.

4. Юдаев Б.Н. Теплопередача. М.: Высшая школа, 1973.-360 с.

5. Кутателадзе С.С. Основы теории теплообмена. - М.: Атомиздат, 1979 - 416 с.

 

Поделиться:

Воспользуйтесь поиском по сайту: