 |
Виды сопряжений, встречающихся в задании
|
|
|
|
| № | Изображение и тип сопряжения | Последовательность выполнения сопряжения | |
Построение касательной к дуге
заданного радиуса

| – проводим из центра дуги (точка О) прямую mпод углом 300; – строим из точки О перпендикуляр к прямой m до пересечения с дугой (точка А); – проводим из точки А прямую n2m. | ||
Сопряжение двух прямых дугой
заданного радиуса

|
– параллельно сторонам угла AB и BC на расстоянии равном радиусу дуги R проводим прямые линии n и m до пересечения в точке О;
– из точки O опускаем перпендикуляры на сопрягаемые стороны. Точки D и E являются точками сопряжения;
| ||
Внешнее сопряжение прямой
линии с дугой окружности

| – из центра О строим дугу радиусом R2= R+R1, где R1 – радиус сопряжения; – на расстоянии R1 от заданной прямой n проводим параллельную прямую m; – определяем центр О1 сопряжения как результат пересечения дуги окружности радиусом R2= R+R1 с прямой m; – из точки O1 опускаем перпендикуляры на сопрягаемые прямую m и дугу (точки сопряжения A и B); – из центра О1 строим дугу AB сопряжения радиусом R1. |
Продолжение табл. 12
| № | Изображение и тип сопряжения | Последовательность выполнения сопряжения |
Внутреннее сопряжение прямой с дугой окружности

| – из заданного центра заданной дуги окружности строим дугу радиусом R2 = R–R1, где R1 – радиус сопряжения; – на расстоянии R1 от заданной прямой n проводим прямую m параллельно n до пересечения в точке О1 (центр сопряжения); – определяем точки сопряжения, для чего из полученного центра О1 опускаем перпендикуляр на прямую n, а через точки О и О1 проводим линию до пересечения с заданной дугой (точки сопряжения А и В); – из полученного центра О1 проводим дугу AB сопряжения радиусом R1. | |
Внешнее сопряжение двух дуг
окружности третьей дугой

| – из центров дуг окружностей О и О1 радиусами R3=R+R2 и R4=R1+R2, соответственно, проводим дуги до их пересечения в точке О2; – соединяем центр сопряжения О2 с центрами дуг окружностей О и О1 прямыми линиями О2О и О2О1 до пересечения с дугами окружностей в точках А и В (точки сопряжения); – из центра сопряжения О2 радиусом R2 проводим дугу между точками сопряжения A и B. |
ПОШАГОВОЕ ВЫПОЛНЕНИЕ ЗАДАНИЯ
|
|
|
Пример решения задачи 1
Исходные данные для задачи 1 выбираются из табл. 1.
Построение овала по двум осям осуществляется в следующей последовательности (рис. 8):
– проводим осевые линии, на которых откладываем отрезки AB и CD, равные большой и малой осям овала (рис. 8а);
– откладываем на малой оси расстояние OE=OA и соединяем точки A и C;
– откладываем на отрезке AC отрезок CF=CE;
– делим отрезок AF пополам;
– проводим через точку K прямую перпендикулярную AF до пересечения с большой и малой осями овала в точках O1 и O2;
– строим зеркальное отображение точек O1 и O2 (точки O3 и O4) и прямой О2К;
– проводим из точки О4 прямые линии через точки О1 и О3;
– проводим из точек O2 и O4 дуги радиусом R= O2C, а из точек O1 и O3 дуги радиусом R1=O1A до их пересечения с прямыми, проведенными через центры дуг (рис. 8б).

а) б)
Рис. 8
Построение эллипса по двум осям выполняется в следующей последовательности (рис. 9):

а) б)
Рис. 9
– проводим осевые линии, на которых симметрично от точки O пересечения откладываем отрезки AB и CD, равные большой и малой осям эллипса (рис. 9а);
– строим две концентрические окружности радиусами равными половине осей эллипса с центром в точке пересечения осей;
– делим окружность на двенадцать частей;
|
|
|
– проводим через полученные точки лучи-диаметры;
– проводим из точек пересечения лучей с соответствующими окружностями прямые линии параллельно осям эллипса до их взаимного пересечения;
– соединяем полученные точки плавной кривой линией при помощи лекал (рис. 9б). При построении лекальной кривой линии необходимо располагать лекало так, чтобы соединялось как минимум четыре-пять точек.
Последовательность построения параболы 1 следующая (рис. 10.):
– проводим горизонтальную линию длиной равной L;
– делим горизонтальную линию на 10 равных частей (точки 0,1,2…,10) и проводим через полученные точки перпендикуляры (теоретические шпангоуты). Откладываем на носовом перпендикуляре (точка 0) аппликату hн, ана кормовом перпендикуляре аппликату hк=0,5hн (точка 10);
– делим носовой и кормовой перпендикуляры на 5 равных частей (точки 0,1,2,…,5 на носовом перпендикуляре и 5,6,…,10 на кормовом перпендикуляре);
– соединяем середину горизонтальной линии (точка 5) с точками, лежащими на носовом и кормовом перпендикулярах. Точки пересечения теоретических шпангоутов с соответствующими линиями, например, шпангоута 3 с линией 53 будут точками палубной линии (рис. 10а);
| а) б) | 
|
Рис. 10
– соединяем при помощи лекала полученные точки плавной кривой линией (рис. 10б).
Парабола (погибь палубы) вычерчивается в таком порядке (рис. 11):
– проводим горизонтальную линию длиной равной В;
– делим горизонтальную линию на 8 равных частей (точки 0,1,2…,8) и проводим через полученные точки перпендикуляры (батоксы). Откладываем на бортовых батоксах (точки 0 и 8) аппликату h=hп;
– делим бортовые батоксы на 4 равные части (точки 0,1,2,3,4 и 4,5,6,7,8);
– соединяем середину горизонтальной линии (точка 4) с точками, лежащими на бортовых батоксах. Точки пересечения батоксов с соответствующими линиями,
(например, батокса 3 с линией 4-3), будут точками палубной линии в поперечном разрезе (рис. 11а);
– соединяем с помощью лекала полученные точки плавной кривой линией (рис. 11б).
| а) б) | 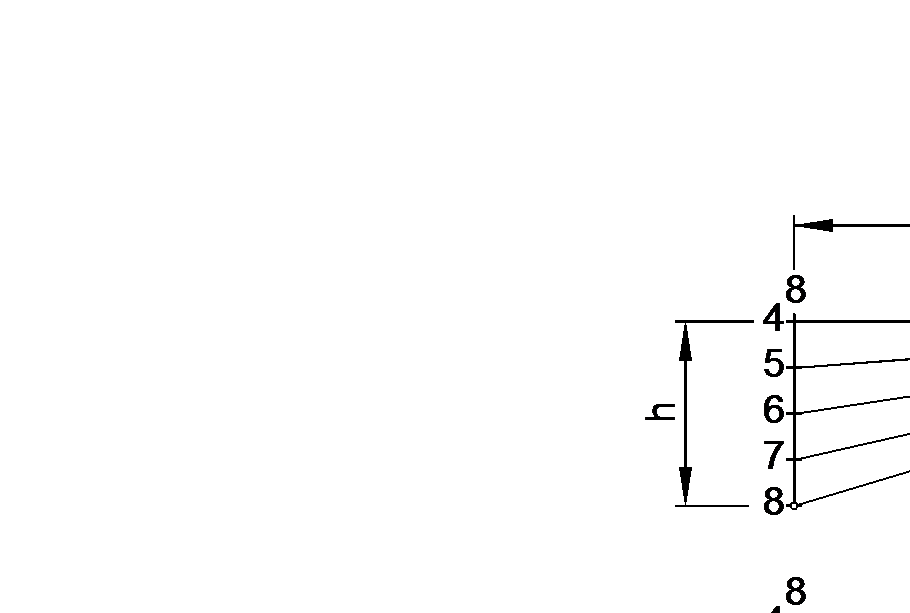
|
Рис. 11
Пример решения задачи 2
Исходные данные для задачи 2 выбираются из табл. 2.
Построение полособульба несимметричного (рис. 12а) выполняется в такой последовательности.
|
|
|
1. Вычерчиваем линии внешнего контура полособульба с толщиной стенки s (рис. 12б);
2. Выполняем скругление наружной грани полки с наружной стороной стенки полособульба, т.е. сопряжение двух прямых линий дугой радиусом r (рис.12в). Последовательность сопряжения см. табл. 12 п.2.
3. Скругляем верхнюю и внутреннюю грани полок полособульба, предварительно построив внутреннюю грань.
3.1. Выполняем скругление правой части полки радиусом r (см. табл.12 п. 1).
3.2. Строим внутреннюю грань полки (рис. 12в). Последовательность построения см. табл.12 п. 1.
4. Выполняем сопряжение внутренней стенки полособульба с нижней гранью полки (рис. 12г). Последовательность сопряжения см. табл. 12 п. 2.
5. Удаляем вспомогательные линии построения и обводим полученный контур профиля сплошной толстой линией (рис. 12д).
6. Проставляем размеры в соответствии с ГОСТ 2.307 – 2011.

|
| а) б) в) |

|
| г) д) е) Рис. 12 |
При нанесении размеров следует учитывать такие правила:
– все буквенные обозначения заменяются соответствующими числовыми величинами;
– при нанесении размера r перед числом следует поставить знак радиуса R; 
– вершина знака уклона ∠ должна быть направлена в сторону уклона.
7. Выполняем штриховку контура под углом 450 (рис. 12е).
Примечание: уклон обозначается знаком ∠ с указанием угла в градусах, например, ∠300.
Полособульб симметричный, (рис. 13а), представляет собой зеркальное отображение полособульба несимметричного, поэтому построение полособульба симметричного аналогично построению приведенному в разделе 4.2 за исключением п.2. Последовательность построения полособульба симметричного приведена на рис. 13.
Пример решения задачи 3
Исходные данные для задачи 3 выбираются из табл. 3.
На рис. 14 показано поэтапное построение крюка с конусностью 1:5. Конусность – это отношение диаметра окружности (D) основания конуса к его высоте (H) для полных конусов или отношение разности диаметров двух поперечных сечений конуса (D и d) к расстоянию между ними (L) для усеченных конусов.
|
|
|
1. Проводим оси и из центра О строим основную окружность внутреннего очертания радиусом R=D/2 и нижнее основание шейки крюка d с центром в точке А (рис. 14а).
2. Строим шейку крюка так:
– откладываем на вертикальной оси от точки А пять отрезков равных диаметру нижнего основания d;
– соединяем полученную точку с концами нижнего основания шейки;
– откладываем от оси отстояние верхнего основания шейки крюка и строим верхнее основание шейки (рис. 14б).
– проводим из точки О луч n под углом 450;
– делаем из точки N радиусом R1 засечку на луче n (точка О1);
4. Строим сопряжение внешней окружности с правым прямолинейным контуром верхней части крюка дугой радиуса R2 (рис. 14г). Построение сопряжения см. в табл.12 п.3.
5. Строим дугой радиусом R1сопряжение основной окружности диаметром D с левым прямолинейным контуром верхней части крюка дугой радиусом R1 (рис. 14д). Построение сопряжения см. в табл. 12 п.3.
– делаем засечку из центра О радиусом D/2 + R1. Точка сопряжения Е основной окружности лежит на линии центров ОО4. Из центра О4 проводим дугу R1, начиная от точки Е.
7. Строим дугу радиусом R3, ограничивающую носик крюка (рис.14ж). Носик крюка должен касаться прямой f, проведенной на расстоянии m от горизонтальной оси. Построение дуги см. табл.12 п.4.
8. Определяем центр О6 дуги радиуса R1, сопрягающей носик крюка с внешним контуром крюка (рис. 14з). Последовательность построения см. в табл.12 п.5.
10. Все буквенные обозначения размеров, проставленные на рис. 14, на чертеже заменяем числовыми величинами (рис. 1).

|
| а) б) в) |

|
| г) д) е) |
Рис.13

|
| а) б) в) |

|
| г) д) е) |

|
| ж) з) и) |
Рис. 14
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Как выполняется деление окружности на равные части?
2. Что характеризует величина, называемая уклоном?
3. Что характеризует величина, называемая конусностью?
4. Как выполняется сопряжение двух пересекающихся прямых линий дугой заданного радиуса?
5. Как выполняется сопряжение прямой линии и дуги дугой заданного радиуса?
6. Как выполняется внешнее сопряжение двух дуг дугой заданного радиуса?
7. Как построить эллипс по большой и малой осям?
8. Как построить параболу?
ЗАКЛЮЧЕНИЕ
В результате выполнения расчетно-графического задания студенты научатся выполнять геометрические построения и усвоят:
– основные правила оформления чертежей;
– правила использования линий на чертежах;
|
|
|
– построение кривых второго порядка;
– нанесение линий штриховки;
– построение уклона и конусности;
– построения сопряжений, лекальных и коробовых кривых линий.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Геометрические построения на чертежах: метод. указания для студентов технических специальностей дневной и заочной форм обучения./ Сост. А.Ф. Медведь, В.Г. Середа. – Севастополь: СевНТУ, 2012. – 20 с.
2. Ковтун В.Н. Справочные материалы для выполнения чертежей приборомашиностроения: справочник / В.Н. Ковтун. – Севастополь: СевНТУ, 2002. – 132 с.
3. Левицкий В.С. Машиностроительное черчение и автоматизация выполнения чертежей / В.С. Левицкий. – М.: Высшая школа, 2001. – 428 с.
4. Матвеев В.Г. Справочник по судостроительному черчению / В.Г. Матвеев, В.Д. Борисенко. - Л.: Судостроение, 1983. – 242 с.
5. Середа В.Г. Инженерная графика. Практикум для студентов: учеб.пособие / В.Г. Середа, А.Ф. Медведь. – Севастополь: СевНТУ, 2011. – 230 с.
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
НА ЧЕРТЕЖАХ
Методические указания
Составители: Медведь Анатолий Феодосьевич
Середа Владимир Григорьевич
Технический редактор – Р.В. Дмитриева
Подписано к печати 25.03.16. Изд. № 206/15. Зак. 385/ 2015. Тираж 75 экз.
Объем 3,5 п.л. Усл. печ. л. 3,25. Уч.-изд. л. 3,430.
Формат бумаги 60 х 84 1/8
РИИЦМ ФГаоУВО «Севастопольский государственный университет»
|
|
|


