Главная | Обратная связь | Поможем написать вашу работу!

Параметры воздушных и кабельных ЛЭП

ЛАБОРАТОРНАЯ РАБОТА № 1. ИССЛЕДОВАНИЕ ЛИНИИ ЭЛЕКТРОПЕРЕДАЧ

Цель работы. Изучение параметров ЛЭП и их влияния на характеристики передачи мощности

Теоретическая часть

Параметры воздушных и кабельных ЛЭП

К электрическим параметрам ЛЭП относятся сопротивления и проводимости проводов ВЛ и жил кабелей.

Активное сопротивление провода или жилы кабеля больше омического сопротивления вследствие поверхностного эффекта, однако это отличие несущественно для токов промышленной частоты. В справочной литературе приводятся погонные (на 1 км) сопротивления проводов и кабелей постоянному току r₀ при температуре 20°С. При необходимости это сопротивление можно пересчитать к любой температуре по выражению

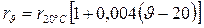. (1.1)

Индуктивное сопротивление фазы ЛЭП обусловлено противодействием ЭДС самоиндукции и влиянием взаимоиндукции соседних фаз. Это влияние частично компенсирует ЭДС самоиндукции, следовательно, результирующее индуктивное сопротивление

X = X_L – X_M, (1.2)

где: X_L – индуктивное сопротивление самоиндукции;

X_M – индуктивное сопротивление взаимоиндукции.

С удалением фаз друг от друга уменьшается взаимная индуктивность и X ® X_L.

Погонное индуктивное сопротивление фазы линии определяется по выражению

, Ом/км, (1.3)

где: w – круговая частота, с^–1;

D_сг – среднегеометрическое расстояние между проводниками линии, м;

d – диаметр провода, мм;

m_r – относительная магнитная проницаемость материала жилы.

Для проводов из цветных металлов (m_r» 1) при f = 50 Гц:

. (1.4)

С ростом номинального напряжения ЛЭП среднегеометрическое расстояние между фазами увеличивается сильнее, чем диаметр провода, и x₀ растёт. Средние значения x₀ находятся в пределах 0,38 … 0,44 Ом/км. В приближённых расчётах x₀ можно принимать равным 0,4 Ом/км.

Провода ВЛ находятся в разных положениях относительно друг друга и земли, поэтому индуктивные сопротивления фаз несколько различаются между собой. Для выравнивания сопротивлений фаз применяют транспозицию проводов. Как правило, это выполняется для ВЛ, длина которых свыше 100 км, так как при меньших длинах несимметричность сопротивлений фаз оказывается незначительной.

У КЛ вследствие близости токоведущих жил индуктивное сопротивление в несколько раз ниже, чем у ВЛ, и в среднем составляет:

§ у трёхжильных кабелей напряжением до 1 кВ 0,06 Ом/км

§ то же, напряжением 6 … 10 кВ 0,08 Ом/км

§ то же, напряжением 35 … 220 кВ 0,15 Ом/км

Ёмкостная проводимость линий обусловлена наличием ёмкостей между проводниками фаз линий, а также между проводниками и землёй.

Емкостная проводимость одной фазы учитывает междуфазные и фазные ёмкости. Погонная ёмкостная проводимость ВЛ определяется по выражению

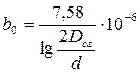, См/км. (1.5)

Среднее значение b₀ для ВЛ напряжением 110 … 220 кВ составляет
2,7 мкСм/км.

У КЛ ёмкостная проводимость больше, чем у ВЛ, вследствие малых расстояний между жилами кабелей.

Активная проводимость линии обусловлена несовершенством изоляции и потерями на корону ВЛ, которые вызваны ионизацией воздуха вокруг проводов, возникающей в случае, если напряжённость электрического поля у поверхности провода превышает электрическую прочность воздуха. Особенно сильно провода коронируют в сырую погоду и при атмосферных осадках.

Коронный разряд на ВЛ снижает КПД ЛЭП, способствует усилению окисления поверхности проводов и является источником радиопомех. Поэтому при сооружении ВЛ применяют провода, диаметры которых при данном номинальном напряжении создают напряжённость электрического поля меньшую, чем требуется для заметного развития коронного разряда, и позволяют не считаться с короной для ВЛ напряжением до 220 кВ. При напряжении 330 кВ и выше средством снижения потерь на корону является расщепление фаз (т. е. выполнение каждой из фаз ВЛ несколькими проводами), однако эти потери всё же остаются большими и их нужно учитывать.

Проводимость, обусловленная короной, является переменной величиной, так как зависит от влажности воздуха и других метеорологических факторов. Усреднённое за год значение активной проводимости можно получить по статистическим данным для каждой ВЛ через средние потери на корону:

. (1.6)

где D P_кор.ср – среднегодовые потери на корону ((3 – 30) кВт/км для ВЛ 330 – 1150 кВ).

Для расщеплённой фазы ВЛ погонные сопротивления и ёмкостная проводимость вычисляются по выражениям:

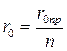; (1.7)

; (1.8)

, (1.9)

где: n – число проводов в фазе;

r_0пр – погонное сопротивление одного провода;

d_экв – эквивалентный диаметр расщеплённого провода в фазе:

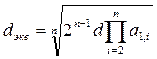(1.10)

a_1,_i – расстояние между проводами в фазе.

Схемы замещения ЛЭП

Каждая фаза ЛЭП может быть представлена в виде четырёхполюсника (рис. 1.1).

Рис. 1.1. Схема замещения ЛЭП в форме четырёхполюсника

Уравнения четырёхполюсника, связывающие напряжения и токи на его входе и выходе, могут быть записаны в виде:

. (1.11)

Четырёхполюсник, моделирующий ЛЭП, является пассивным и симметричным. ЛЭП – объект с распределёнными параметрами, который описывается уравнениями длинной линии, учитывающими волновой характер распространения тока и напряжения вдоль линии:

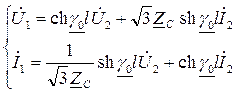, (1.12)

где: 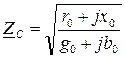– волновое сопротивление линии;

–коэффициент распространения волны;

a₀ – коэффициент затухания волны;

b₀ – коэффициент фазы.

Коэффициенты четырёхполюсника, моделирующего ЛЭП, определяются по выражениям:

; (1.13)

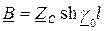; (1.14)

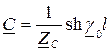. (1.15)

Для расчётов ЛЭП обычно используют симметричную П-образную схему замещения (рис. 1.2), параметры которой связаны с коэффициентами четырёхполюсника соотношениями:

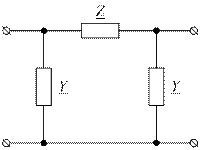
Рис. 1.2. П-образная схема замещения

; (1.16)

; (1.17)

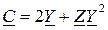. (1.18)

Отсюда можно определить параметры П-образной схемы замещения ЛЭП:

; (1.19)

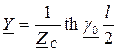. (1.20)

Для ЛЭП длиной менее 300 км можно принять sh g₀» g₀ и th g₀» g₀, поэтому

, (1.21)

. (1.22)

Таким параметрам соответствует схема замещения, приведённая на рис. 1.3.

Рис. 1.3. П-образная схема замещения ЛЭП

Баланс мощностей в ЛЭП

Для ЛЭП (рис. 1.4) можно записать уравнение баланса мощностей:

Рис. 1.4. Мощности в схеме замещения ЛЭП

, (1.23)

где: – мощность в начале линии;

– мощность в конце линии;

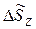– потери мощности в продольном сопротивлении линии;

Q_C₁ и Q_C₂ – зарядные мощности начала и конца линии.

Потери мощности в продольном сопротивлении линии Z = R + jX определяются протекающим по нему током:

. (1.24)

Ток может быть выражен через мощность и напряжение как в начале, так и в конце линии:

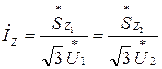. (1.25)

Выражение потерь мощности через поток мощности в линии:

. (1.26)

Потери активной и реактивной мощностей:

; (1.27)

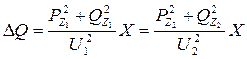. (1.28)

Зарядные мощности начала и конца ЛЭП:

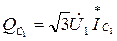; (1.29)

, (1.30)

где зарядные токи начала и конца ЛЭП

; (1.31)

. (1.32)

Окончательно

; (1.33)

. (1.34)

Величина 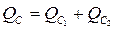называется зарядной мощностью ЛЭП. Потери реактивной мощности в продольном сопротивлении ЛЭП и зарядная мощность имеют противоположные знаки, но могут быть близки по абсолютной величине в отдельных режимах работы ЛЭП.

Натуральная мощность ЛЭП

Рассмотрим участок ЛЭП длиной Dl при r₀ = 0 и g₀ = 0 (линия без потерь).

Потери реактивной мощности на индуктивном сопротивлении участка линии

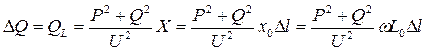. (1.35)

Генерация реактивной мощности на участке

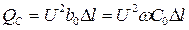(1.36)

не зависит от величины передаваемой мощности.

Если принять нагрузку в конце линии чисто активной (Q = 0), то при определённом значении активной мощности нагрузки P будет выполняться равенство

. (1.37)

Мощность, передаваемую в таком режиме, называют натуральной мощностью P_нат, а сам режим – режимом передачи натуральной мощности.

Условие передачи натуральной мощности можно записать в виде

; (1.38)

; (1.39)

откуда

. (1.40)

В реальной линии, при r₀ ¹ 0 и g₀ ¹ 0, потери активной мощности в линии при Q = 0 будут наименьшими:

, (1.41)

а при P = P_нат линия будет работать с наибольшим КПД.

В натуральном режиме работы линии напряжения и токи в любой точке линии оказываются неизменными по модулю.

Порядок выполнения работы

1. Рассчитать активное R, индуктивное X сопротивления и ёмкостную проводимость B исследуемой ВЛ согласно данным своего варианта (табл. 1.2):

;

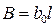2. Запустить RastrWin. Если появилось окно первого запуска (рис. 1.5), необходимо щёлкнуть мышью по кнопке Продолжить.

Рис. 1.5. Окно первого запуска программы

3. Выбрать меню Расчеты»Параметры»Режим. В открывшемся окне Режим установить параметр Точность расчёта (dP) равным 0,01. Закрыть окно Режим.

4. Открыть таблицу Узлы (меню Открыть»Узлы»Узлы) (рис. 1.6).

Рис. 1.6. Таблица Узлы

5. В столбце «Номер узла» (Номер) ввести 1. В столбце «Номинальное напряжение» (U_ном) установить номинальное напряжение в кВ согласно варианту. В столбце «Заданный модуль напряжения» (V_зд) установить значение напряжения источника питания (на 5 % больше номинального напряжения). В столбце «Тип узла» (Тип) из выпадающего меню выбрать База.

6. Добавить строку в таблице Узлы нажатием кнопки Добавить (или комбинацией клавиш Ctrl + A). В столбце «Номер узла» (Номер) ввести 2. В столбце «Номинальное напряжение» (U_ном) установить номинальное напряжение в кВ согласно варианту. В столбце «Тип узла» (Тип) из выпадающего меню выбрать Нагр.

7. Открыть таблицу Ветви (меню Открыть»Ветви»Ветви) (рис. 1.7). Щелкнув правой кнопкой мыши на заголовке столбца «Поток P начале ветви» (P_нач), выбрать в контекстном меню пункт Поток P начале ветви |P_нач| - (pl_ip), [МВт]. В открывшемся окне vetv[Ветви].pl_ip[P_нач] на закладке Параметры установить в поле Точность значение 2. Выполнить аналогичную операцию для столбца «Поток Q в начале ветви» (Q_нач).

Рис. 1.7. Таблица Ветви

8. В столбце «Номер начала» (N_нач) ввести 1. В столбце «Номер конца» (N_кон) ввести 2. В столбцах «Сопротивление R» (R), «Сопротивление X» (X) и «Проводимость на землю мкСим» (B) установить значения рассчитанных параметров ВЛ (R, Ом; X, Ом, B, мкСм).

9. Открыть таблицу Токовая загрузка ЛЭП (меню Открыть»Ветви»Токовая загрузка ЛЭП) (рис. 1.8).

Рис. 1.8. Таблица Токовая загрузка ЛЭП

10. Смоделировать режим холостого хода ЛЭП. Запустить расчёт режима нажатием кнопки Режим на панели инструментов, или выбором в меню пункта Расчеты»Режим, или нажатием F5. Записать результаты моделирования в таблицу (табл. 1.1). (Напряжение в конце линии U₂ – таблица Узлы, столбец «Расчётный модуль напряжения» (V_рас) для узла 2; Токи в начале и конце линии I₁, I₂ – таблица Токовая загрузка ЛЭП, столбцы «Ток начала ветви» (I_нач) и «Ток конца ветви» (I_кон); мощности в начале ветви P₁, Q₁ – таблица Ветви, столбцы «Поток P начале ветви» (P_нач) и «Поток Q в начале ветви» (Q_нач)). ВНИМАНИЕ! Знаки мощностей в таблице Ветви отрицательны при направлении мощности от начала ветви к концу и положительны при обратном направлении. В табл 1.1 их следует записывать с обратным знаком.

Таблица 1.1. Таблица для записи результатов измерений.

№ опыта

Задано

Измерено

Вычислено

P₂, МВт

Q₂, Мвар

U₁, кВ

U₂, кВ

I₁, А

I₂, А

P₁, МВт

Q₁, Мвар

S₁, МВ×А

S₂, МВ×А

DP, кВт

DQ, квар

h, %

DU, кВ

dU, %

…

11. Смоделировать нагрузочный режим работы ЛЭП при чисто активной нагрузке. Задавая активную мощность в конце линии P₂ (столбец «Мощность нагрузки P» (P_н) для узла 2), равной (0,2; 0,4; 0,6; 0,8; 1) P_max, получить результаты расчёта режимов и занести их в таблицу 1.1.

12. Смоделировать нагрузочный режим работы ЛЭП при активно-индуктивной нагрузке с tg j = 0,25. Задавая активную мощность в конце линии P₂ такой же, как в п. 11, задавать реактивную мощность в конце линии Q₂ равной 0,25 P₂. Получить результаты расчёта режимов и занести их в таблицу 1.1.

13. Смоделировать нагрузочный режим работы ЛЭП при активно-индуктивной нагрузке с tg j = 0,5.Повторить п. 12, задавая Q₂ равной 0,5 P₂.

Воспользуйтесь поиском по сайту: