Амплитудно-модулированные сигналы

Генераторные измерительные схемы

Схемы с генерированием синусоидальных колебаний

Частота синусоидальных колебаний генератора является вполне определенной и при соответствующих условиях может равняться резонансной частоте контура, состоящего из катушки с индуктивностью L₀и конденсатора емкостью С₀, соединенных последовательно или параллельно. На резонансной частоте F₀ сопротивление контура оказывается чисто активным, и F₀ опре­деляется выражениями:

а) для последовательного колебательного контура:

б) для параллельного колебательного контура:

Здесь Q_L — добротность катушки, — сопротивле­ние катушки, , обычно Q²l>>1, так что для обоих кон­туров

Когда индуктивный или емкостной датчик является элемен­том резонансного контура генератора, вариации его реактивно­го сопротивления вызывают соответствующие изменения часто­ты колебаний. В зависимости от типа датчика и в предположе­нии, что амплитуда изменений его реактивного сопротивления невелика, для соответствующих изменений частот UKUKU AF справед­ливы соотношения:

т.е.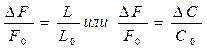

Если измеряемая величина изменяется относительно значения mо по гармоническому закону с амплитудой колебаний, при ко­торой характеристику преобразования датчика можно считать линейной, а чувствительность равной S,тo m(t)=m0+т1coswt, a ▼L или ▼C=Sm1c oswt. Мгновенное значение частоты генера­тора при этом

где в зависимости от типа датчика.

Частота генератора модулируется по закону изменения из­меряемой величины. В общем случае выходное напряжение ге­нератора можно записать в виде 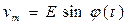, где ф(t) — мгновенное значение фазы.

При модуляции в каждый момент времени

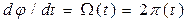
откуда

т. е.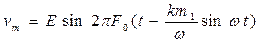

Выходной сигнал генератора описывается, следовательно, выра­жением

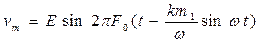
или, подставляя коэффициент частотной модуляции 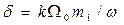, подучим

Когда речь идет о передаче информации, исходящей от мно­гих датчиков с реактивным сопротивлением, сигнал каждого датчика модулирует свою поднесущую частоту. Совокупность промоделированных таким образом сигналов модулирует затем общую несущую частоту (рис. 3.24).

Измерительные схемы релаксационного типа

Наиболее часто применяемой схемой такого вида является схема мультивибратора с самовозбуждением (рис. 3.25), пред­ставляющего собой генератор прямоугольных импульсов. Ча­стота F этих импульсов связана с параметрами элементов схе­мы соотношением

где константа а зависит от конкретной реализации схемы.

Емкость С или сопротивление R может быть переменной ве­личиной соответствующего датчика:

C = C0+▼C или R=R0+▼R

 

 

и, следовательно,

Как и в случае генератора синусоидальных колебаний, частота мультивибратора модулируется по закону изменения выходной переменной датчика.

Характеристики выходного сигнала измерительной схемы

Частотный спектр сигнала

Выходной сигнал измерительной схемы характеризуется •спектром частот, который, с одной стороны, зависит от спектра частот измеряемой величины, а с другой стороны, - от возможностей неискаженного восприятия и передачи этого спектра са­мой схемой и датчиком. Важно передать весь спектр частот из­меряемой величины, если при обработке сигнала мы хотим из­бежать нежелательной потери информации. Действительно, любая электронная аппаратура характеризуется кроме всего прочего полосой пропускания, т. е. совокупностью частот, которые могут быть переданы через тракт измерений и обработки сигнала. Час­тоты, лежащие вне полосы пропускания, сильно ослабляются при обработке. Чтобы избежать потерь информации, требуется обес­печить минимально необходимый диапазон частот спектра сигна­ла, согласуя с этим диапазоном полосу пропускания аппарату­ры. Понятие необходимой полосы пропускания или полезного спектра следует уточнить, так как оно зависит от условий изме­рения и допустимой погрешности. Так, например, измеряемая величина m(t) с периодом Т изменения может быть представле­на рядом Фурье — бесконечной последовательностью гармони­ческих составляющих с амплитудами С_n и частотами nF, где n —целое число, a F — основная частота (первая гармоника), F=1/T. Абсолютно точное отображение m(t) таким рядом тре­бует в общем случае преобразования измеряемой величины в соответствующий сигнал с теоретически бесконечно протяжен­ным спектром (п→α), что достижимо лишь при нереально ши­рокой (бесконечной) полосе пропускания тракта передачи этого

сигнала. Ограничение спектра электронными устройствами, полоса пропускания которых конечна, обязательно приводит к. искажению сигнала.

Можно показать, что при п→α С_n = 0. Максимально допу­стимое искажение сигнала определяет число его гармоник п которые должны сохраниться при обработке сигнала и его пере­даче.

Чтобы охарактеризовать порядок этих величин, можно пока­зать, что в случае сигнала, представляемого последовательно­стью прямоугольных импульсов продолжительностью d и с пе­риодом следования Т (d<<T)_, достаточная для анализа измере­ний ширина спектра имеет порядок 1/d. Так, при d=l0^-6 c до­статочной для анализа оказывается верхняя граничная частота спектра, равная 1 МГц.

С точки зрения снижения частотных искажений при преоб­разовании измеряемой величины более предпочтительны изме­рительные схемы на постоянном токе, однако они пригодны лишь для резистивных датчиков.

Амплитудно-модулированные сигналы

Модуляция по амплитуде без подавления несущей частоты.

В потенциометрической схеме с несимметричным питанием при дифференциальном включении двух резистивных датчиков вы­ходное напряжение схемы равно

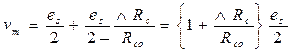
Если датчики линейны и чувствительность S постоянна во всем рабочем спектре частот измеряемой величины, то

т. е. v_m изменяется в функции линейно.

При питании указанной схемы синусоидальным напряжени­ем предыдущее соотношение преобразуется к виду

Если измеряемая величина изменяется по синусоидальному закону (рис. 3.26),

то

где, . a S — чувствительность датчика в динамическом режиме на частоте опоздания.

После элементарных тригонометрических преобразований можно записать:

 

где

Спектр напряжения v_m (рис 3.26, г) содержит частоты 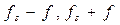. В более общем случае (рис. 3.27), когда изменения измеряемой величины образуют сигнал сложной формы, который может быть представлен как результат наложения друг на дру­га большого числа гармонических составляющих

,

получаем

,

где 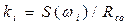. Последнее выражение для v_m можно преоб­разовать к виду

.

Спектр этого напряжения (рис. 3.27, г) содержит частоту f_s питающего напряжения, называемую несущей частотой, ниж­нюю боковую полосу, образованную набором частотf_s — fi, и верхнюю боковую полосу с частотами f_s+fi.

Если f_М — верхняя граничная частота спектра измеряемой величины, то спектр выходного напряжения измерительной схе­мы простирается от f_s—fм до f_s+fм, Поэтому, чтобы передать спектр измеряемой величины, схемы обработки сигнала должны иметь полосу пропускания, равную, по крайней мере, 2fм с центральной частотой f_s.

Если питающее напряжение не гармоническое (см. рис. 3.28), то, представив его рядом Фурье

.

предыдущее выражение для выходного напряжения измеритель­ной схемы

можно преобразовать к виду

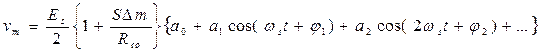
Для общего случая измеряемой величины, описываемой сигна­лом сложной формы, , имеем

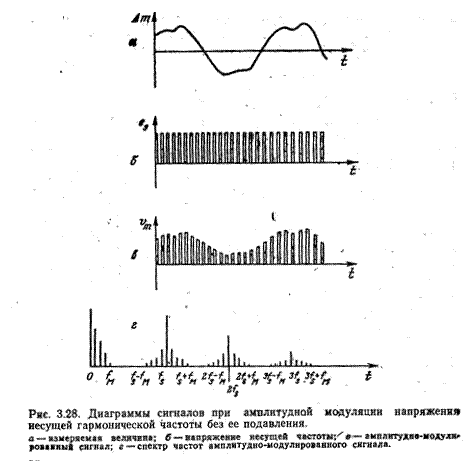
Иначе говоря, v_m есть сумма модулированных по амплитудам членов разложения е_s в ряд Фурье, и спектр напряжения v_m (рис. 3.28, г) включает в себя спектр , который простирается до f_м - верхней граничной частоты измеряемой величины (), набор несущих частот nf_s, (n=1, 2,...), для которых , нижнюю боковую полосу частот до nf_s - fм и верхнюю боковую полосу частот до nf_s + fм.

Чтобы иметь возможность выделить частоты спектра собст­венно измеряемой величины, нет нужды восстанавливать боко­вые полосы несущих частот, т. е.

откуда .

Таким образом, основная частота (частота первой гармони­ки) питающего напряжения должна по меньшей мере вдвое

превосходить верхнюю граничную частоту спектра измеряемой величины.

Модуляция по амплитуде с подавлением несущей. Когда используют мостовую или потенциометрическую схему с сим­метричным питанием, спектр выходного напряжения этих схем не содержит частотных составляющих питающего напряжения.

Например, для дифференциальной схемы с резистивными датчиками имеем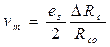

В общем случае (см. рис. 3.29), когда измеряемая величина и питающее напряжение измерительной схемы описываются сложными периодическими функциями, легко установить, что спектр выходного напряжения v_m образован из спектра измеряемой величины с верхней граничной частотой f_м (при условии, что ), нижней боковой полосы частот до nf_s – f_м и верхней бо­ковой полосы частот до nf_s+f_м, за исключением несущих ча­стот nf_s.

Возможность выделить спектр измеряемой величины обеспечивается, как и в предыдущем случае, при выполнении условия

В частном случае питающего напряжения синусоидальной формы (рис. 3.30) частотный спектр v_m составляет от. f_s – f_м до f_s+f_м, но без частоты f _s. В отличие от модуляции по ампли­туде с сохранением несущей, при подавлении последней пико­вые значения v_m не следуют за изменением .

Поделиться:

Воспользуйтесь поиском по сайту: