Квантовая природа агрегатных состояний

Макроскопических объектов

Квантовая механика явилась мощным инструментом теоретического исследования электрических, оптических и других свойств реальных макроскопических объектов. В соответствии с квантово-механическими представлениями электроны в атомах могут находиться на вполне определенных «орбитах», соответствующих различным значениям потенциальной энергии взаимодействия этих электронов с положительно заряженными ядрами. При этом речь по-прежнему идет не о классических орбитах, представляющих собой замкнутые траектории в пространстве, а о «размазанных облаках вероятности» нахождения электронов, которые описываются квадратом модуля Y - функции. Так как потенциальная энергия свободного, т.е. находящегося на большом расстоянии от ядра электрона считается равной нулю, то потенциальная энергия связанных с ядром электронов является отрицательной (напомним, что потенциальная энергия численно равна работе по перемещению заряда, в данном случае отрицательного, из данной точки пространства в бесконечность). Эти возможные значения энергии E_n, (n = 1, 2,...) электронов в атоме можно отложить на вертикальной оси, как показано на рис.7.5,а. Следует отметить, что на самом деле каждой энергии Е_n соответствует не одно, а несколько возможных состояний, отличающихся конфигурацией Y - функций. Только «ближайшее» к ядру состояние с минимальной энергией Е₁ является одиночным, ему соответствует сферически симметричная Y-функция. Уже следующему состоянию с энергией Е₂ соответствуют две различные Y-функции: одна - сферически-симметричная, а модуль другой имеет вид «бублика» и т.д.

Эти возможные состояния заполняются электронами весьма своеобразно. Оказывается, что электроны помимо массы и электрического заряда обладают еще одной физической характеристикой - спином, который можно было бы представить себе как «вращение» электрона вокруг собственной оси, если бы такое представление не было столь вызывающе противоречащим предположению о «точечной» структуре электрона. Тем не менее спин имеет размеренность момента импульса - кг (м/с) м = Дж × с, а его численное значение для электрона равно h/2, где h - постоянная Планка. В связи с этим электроны относятся к элементарным частицам с «полуцелым» спином или фермионам (так как квантово-статистические закономерности их поведения описываются функцией распределения Ферми-Дирака, в отличие от бозонов - частиц с «целым» спином, подчиняющихся квантовой статистике Бозе-Эйнштейна). Для фермионов справедлив фундаментальный принцип Паули, в соответствии с которым в одном квантовом состоянии не может находиться более двух частиц с противоположными направлениями спинов. Поэтому если атом содержит несколько электронов, то они распределяются по разным энергетическим уровням, последовательно заполняя возможные состояния, начиная с «нижнего», ближайшего к ядру. Например, на нижнем энергетическом уровне Е₁ могут находиться только два электрона, спины которых противоположны, на следующем уровне - с энергией Е₂ - восемь электронов и т.д. Как известно, именно такое заполнение электронных оболочек обусловливает химические свойства атомов и их расположение в таблице Менделеева.

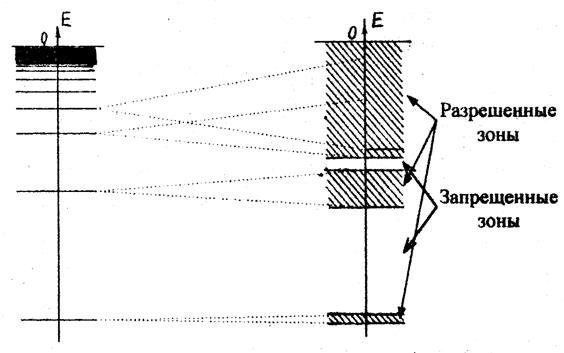
Рис.7.5. Образование энергетических зон в кристалле

Таким образом, можно сказать, что химические, электрические, оптические и другие свойства атомов являются следствием, с одной стороны, дискретной структуры электронных оболочек и, с другой стороны, принципа Паули, определяющего «правила» заполнения этих оболочек электронами.

Рассмотренная квантовая структура атомов хорошо объясняет свойства соответствующих газов. При сближении атомов и молекул, когда вещество переходит в конденсированное состояние (жидкое, твердое), поведение электронов уже нельзя описать дискретными энергетическими состояниями. Весьма полезным в этом случае оказывается представление об энергетических зонах, которые лучше всего понять на примере атомных кристаллов.

Если атомы, обладающие дискретным энергетическим спектром (т.е. дискретными электронными «орбитами»), располагаются на определенных расстояниях друг от друга, образуя кристаллическую решетку, то «глубокие» электронные «орбиты», находящиеся ближе всего к ядру, как правило, не пересекаются, а находящиеся на них электроны остаются «привязанными» каждый к соответствующему ядру. В то же время более удаленные от ядра «орбиты» начинают пересекать друг друга, так что находящиеся на этих «орбитах» электроны становятся «общими» для всех ядер, для всего кристалла в целом. При этом на энергетической диаграмме вместо одного дискретного уровня появляется целая зона возможных значений энергии (см. рис. 7.5,б). Чем сильнее пересекаются дискретные уровни атомов, образующих кристалл, тем шире энергетическая зона. И если для низколежащих уровней получающиеся «разрешенные» зоны энергий оказываются разделенными «запрещенными» зонами, то для удаленных от ядра уровней соответствующие зоны могут начать перекрываться, образуя сплошной энергетический спектр.

Как дискретные «орбиты» отдельных атомов, так и энергетические зоны в кристалле - это только возможные состояния электронов. Заполнение этих состояний осуществляется в соответствии с принципом Паули, так что часть зон может оказаться заполненной полностью, часть - частично, а часть остаться вообще без электронов. Свойства кристалла определяются тем, как заполнена электронами последняя из непустых энергетических зон. Если она заполнена полностью и отделена от следующей за ней пустой зоны достаточно широким (³2 эВ) энергетическим промежутком (запрещенной зоной), то такой кристалл ведет себя как хороший изолятор, не пропускающий электрический ток. Если же запрещенная зона достаточно узкая (£ 2 эВ), то кристалл становится полупроводником, электрическая проводимость которого сильно зависит от температуры. Наконец, если последняя непустая зона заполнена частично, то кристалл является хорошим проводником электрического тока.

Вопросы для самопроверки:

1. С решением какой физической проблемы связано появление квантовой концепции?

2. Что такое корпускулярно-волновой дуализм?

3. Какие постулаты были положены Н.Бором в основу его теории атома?

4. Какой физический смысл имеет введенная Э.Шредингером Y-функция микрочастицы?

5. Что такое принцип неопределенности Гейзенберга?

6. С какими квантовыми принципами связаны основные свойства вещества?