 |
Динамическое представление сигналов
|
|
|
|
Динамическое представление сигналов с помощью функций включения и дельта -функций. Ортогональные сигналы.
Рекомендованная литература:
| 1. Динамическое представление сигнала | Баскаков. РТЦиС | Стр. 16-17 |
| 2. Функция включения | Баскаков. РТЦиС | Стр. 17-19 |
| 3. Дельта –функция | Баскаков. РТЦиС | Стр. 19-21 |
| 4. Ортогональные сигналы | Баскаков. РТЦиС | Стр. 27-34 |
Задача:
Запишите выражение динамического представления с помощью функций включения сигнала вида s(t)=1+4t длительностью 12 мкс для последовательности моментов времени с шагом дискретизации 3 мкс. Изобразить соответствующий график.
Решение задачи:
Если S0=S(0) – начальное значение, то текущее значение сигнала при любом t приближенно равно сумме ступенчатых функций:
(6.1)
где 
- функция включения;
=3 мкс – шаг дискретизации;
=12 мкс – длительность сигнала;
- номер шага.
По полученному выражению построим график (Рисунок 6.8):
Рисунок 6.8 Динамическое представление сигнала.
Сущность спектрального представления сигналов
Сущность спектрального представления сигналов. Спектральное представление периодического и непериодического сигнала.
Рекомендованная литература:
| 1. Спектральное представление сигналов | Баскаков. РТЦиС | Стр. 38 |
| 2. Спектральное представление периодических сигналов | Баскаков. РТЦиС | Стр. 38-40; 42-43 |
| 3. Спектральное представление периодических сигналов | Баскаков. РТЦиС | Стр. 43-47 |
Задача:
Качественно построить графики временных и спектральных диаграмм периодической последовательности прямоугольных импульсов скважностью 2; 4; 2,5 (один под другим). Дать необходимые пояснения вида графиков и его зависимости от периода и длительности импульсов.
|
|
|
Решение задачи:
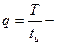(6.2)
скважность сигнала (отношение периода сигнала к длине импульса).
Даны скважности: q1=2; q2=4; q3=2,5.
Если периоды всех трёх сигналов равны, то
Построим их временные диаграммы (Рисунок 6.9):
Рисунок 5.9 Временные диаграммы.
Спектральная диаграмма периодического сигнала – графического изображения коэффициентов ряда Фурье:
(6.3)
где 
основная частота последовательности;
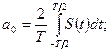(6.4)
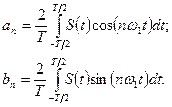(6.5)
Для периодической последовательности прямоугольных импульсов выражения примут вид:
, где А – амплитуда импульса;
Окончательную форму ряда Фурье для данного случая можно записать в виде:
(6.6)
Построим спектральные диаграммы для 3-х случаев:
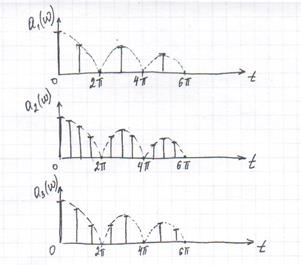
Рисунок 6.10 Спектральные диаграммы.
Корреляционная функция сигналов и её свойства.
Корреляционная функция сигналов и её свойства. Интервал корреляции. Функция корреляции дискретных сигналов.
Рекомендованная литература:
| 1. Корреляционная функция сигналов и её свойства | Баскаков. РТЦиС | Стр. 77-79; Стр. 81 (заг-к 2) |
| 2. Интервал корреляции | Баскаков. РТЦиС | Стр. 169 (абзац 1) |
| 3. Функция корреляции дискретных сигналов | Баскаков. РТЦиС | Стр. 84-85 |
Задача:
Определить и построить график функции корреляции дискретного сигнала вида 1 -1 1 1 -1 1 1 -1. Дать необходимые пояснения вида функции.
Решение задачи:
Функция автокорреляции:
. (5.7)
1) Найдем функцию автокорреляции при нулевом смещении:
| -1 | -1 | -1 | |||||
| -1 | -1 | -1 |
2) Найдем функцию автокорреляции при смещении n=1:
|
| -1 | -1 | -1 | ||||||
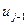
| -1 | -1 | -1 |
3) Найдем функцию автокорреляции при смещении n=2:
|
| -1 | -1 | -1 | |||||||
| -1 | -1 | -1 |
4) Найдем функцию автокорреляции при смещении n=3:
|
| -1 | -1 | -1 | ||||||||
| -1 | -1 | -1 |
|
|
|
5) Найдем функцию автокорреляции при смещении n=4:
|
| -1 | -1 | -1 | |||||||||
| -1 | -1 | -1 |
6) Найдем функцию автокорреляции при смещении n=5:
|
| -1 | -1 | -1 | ||||||||||
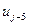
| -1 | -1 | -1 |
7) Найдем функцию автокорреляции при смещении n=6:
|
| -1 | -1 | -1 | |||||||||||
| -1 | -1 | -1 |
8) Найдем функцию автокорреляции при смещении n=7:
|
| -1 | -1 | -1 | ||||||||||||
| -1 | -1 | -1 |
9) Найдем функцию автокорреляции при смещении n=8:
|
| -1 | -1 | -1 | |||||||||||||
| -1 | -1 | -1 |
По значениям, найденным в пунктах 1-9, построим график функции автокорреляции.
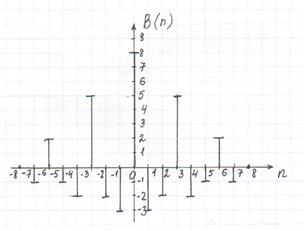
Рисунок 6.11 График функции автокорреляции.
Функция автокорреляции четная (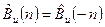
), поэтому при построении можно ограничиться расчетом только одной из симметричных половин.
Энергия дискретного сигнала равна:
|
|
|
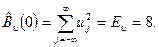
