 |
Цепь с последовательным соединением активного сопротивления индуктивности и емкости. Резонанс напряжений.
|
|
|
|
i = IM sinWt
u = uR + uL + uC
Рассмотрим 3 случая:
1) UL > UC; XL > XC
2) UL < UC: XL < XC
3) UL = UC: XL = XC
1 случай UL > UC; XL > XC.
; 
; 
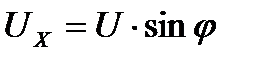
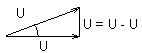
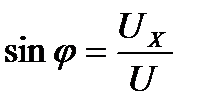
Умножив каждую сторону на ток, получим треугольник мощностей.
, 
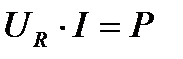
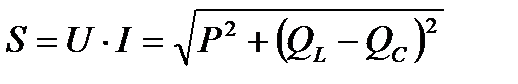
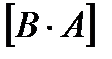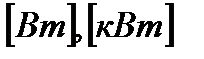
Коэффициент мощности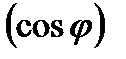 
показывает, какую долю от полной мощности составляет активная мощность.
Разделив каждую сторону треугольника напряжений на ток, получим треугольник сопротивлений.
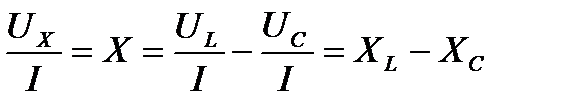
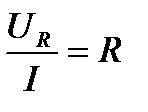
- полное сопротивление цепи
, 
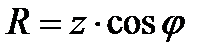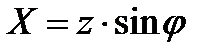
2-й случай UL < UC, XL < XC
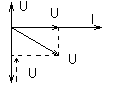
Все остальное, в принципе то же самое.
3-й случай: UL = UC: XL = XC
В последовательной цепи, состоящей из активного сопротивления, индуктивности и емкости, при равенстве реактивных сопротивлений XL и XC резонанс напряжений.
Т.к. 
а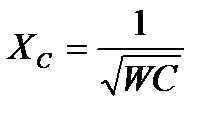 
, то при резонансе 
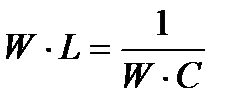или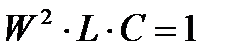 
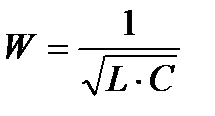- угловая скорость
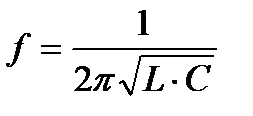- частота
Установлено, что в контуре без потерь, подключенном к источнику постоянного напряжения, возникает переменный ток с угловой частотой собственных колебаний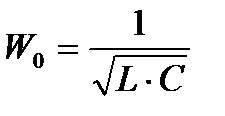 
Т.е резонанс наступает, если частота напряжения источника питания W совпадает с частотой собственных колебаний контура W0, при этом X=XL-XC=0 т.е реактивное сопротивление равно нулю.
При резонансе сопротивление любого из реактивных участков цепи:
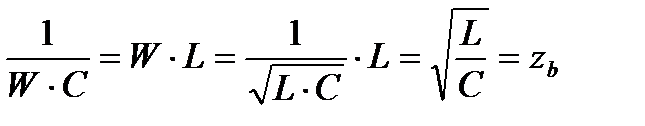
Принято называть волновым сопротивлением.
Величина 
- называется добротностью контура.
Полное сопротивление цепи при резонансе напряжений:
Равно активному сопротивлению цепи, и следовательно, наименьшее из всех возможных при изменении частоты f.
Ток в цепи (действующее значение) при резонансе достигает максимума и совпадает с напряжением по фазе.
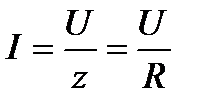
При резонансе индуктивное напряжение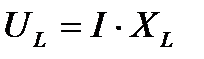 
и емкостное 
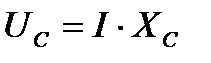, сдвинутые по фазе на половину периода, равны по величине;
Напряжение на зажимах цепи U равно активному напряжению 
.
|
|
|
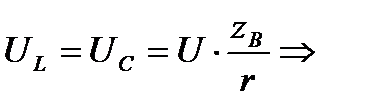при zB > R напряжение UL и UC больше приложенного к зажимам цепи!
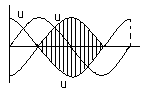
Настройка цепи в зажим резонанса напряжений может быть выполнена следующим образом:
1) при неизменной индуктивности изменением емкости
2) при неизменной емкости изменением индуктивности
3) при неизменной емкости и индуктивности изменением частоты.
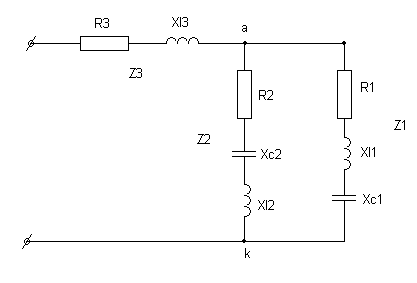
Расчет разветвленной электрической цепи символическим методом.
Дано: Разветвленная электрическая цепь имеет параметры:
U=127B, R1 = 3 Ом; R2 = 4 Ом; R3 = 5 Ом
XL1 =5 Ом; XL2 =2 Ом; XL3 =8, 66 Ом
Xe1 = 1 Ом; Xe1 = 70 Ом
Цепь питается от генератора синусоидального напряжения частотой f = 50 Гц. Определить токи и напряжения ветвей, составить баланс мощностей и построить векторную диаграмму.
РЕШЕНИЕ
1) Выражаем значения напряжения и сопротивлений цепи в комплексной форме:
U = 
Z 1=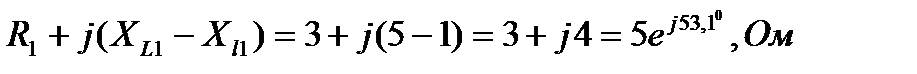 
Z 2= 
Z 3=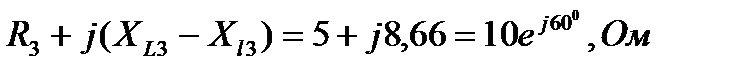 
2) Находим полное комплексное сопротивление всей цепи:
Z = Z 3 + Z ak
Z ak =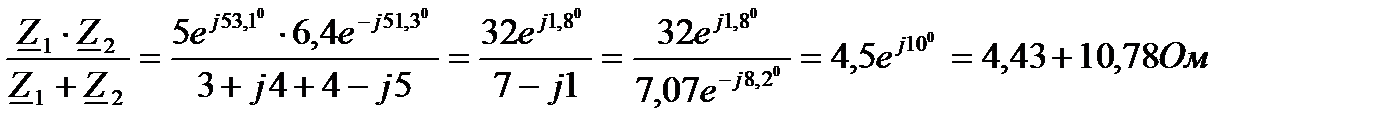 
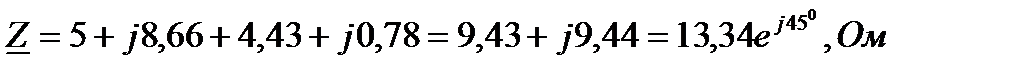
3) Ток в неразветвленной части цепи
4) Токи в параллельных ветвях:
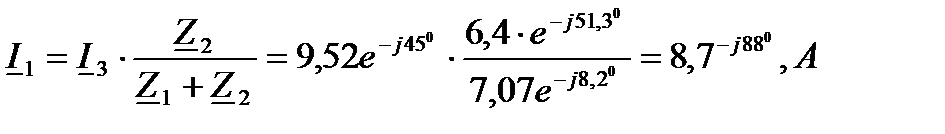
5) Напряжение на участках
6) Мощность цепи и отдельных участков
Где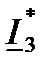 
, комплекс сопряженный I 3.
Два комплекса называются сопряженными, если они имеют одинаковые модули и равные по величине, но противоположные по знаку аргументы.
если 
, то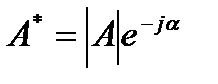 
Активная мощность P равна 855, Вт
Реактивная мощность Q равна 855, вар.
7) составляем баланс мощностей:
8)Строим векторную диаграмму.
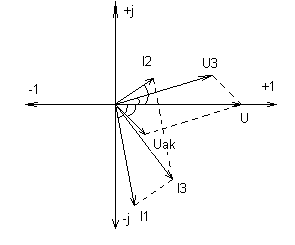
Резонанс токов.
При параллельном соединении элементов колебательного контура (индуктивности и ёмкости) может иметь резонанс токов, для которого характерна возможность возникновения токов в индуктивной и ёмкостной ветвях, значительно превышающий ток, получаемый от источника.
Закон Ома для параллельного соединения выражается формулой 
Общее условие резонанса токов – это равенство емкостной и индуктивной реактивных проводимостей
|
|
|
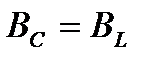
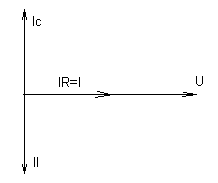
В этом случае I = UG, т.е. при резонансе общий ток I принимает минимальное значение и совпадает по фазе с напряжением.
В этих условиях источник переменного тока и провода, соединяющие его с колебательным контуром, совершенно разгружены от реактивного тока, который замыкается в кольце, образуемом индуктивностью и ёмкостью. Цепь ведет себя как бы е одним резистивным элементом.
Мгновенные мощности индуктивной и емкостной ветвей также противоположны по фазе, т.е. когда энергия накапливается в магнитном поле индуктивности, она убывает в электрическом поле емкости. В такой системе энергия колеблется между индуктивностью и емкостью, а источник от этих колебаний разгружен, и он только дает энергию, нужную для покрытия потерь в активной ветви.
если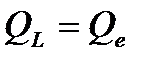 
то S=P
В случае резонанса токов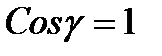 
Следовательно, резонанс токов можно использовать для повышения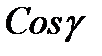 
приемника. Для этого к приемнику с преобладающим индуктивным сопротивлением параллельно подключается конденсатор.
Работать с меньшими токами и большим 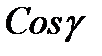выгоднее. (В первую очередь для предприятий занимающихся передачей электрической энергии, т.к. в этом случае уменьшаются потери от нагрева проводов.)
Лекция №4.
|
|
|
