Количественные показатели надежности

Лекция 1

ОСНОВНЫЕ СВЕДЕНИЯ О НАДЕЖНОСТИ БУРОВОГО И НЕФТЕГАЗОПРОМЫСЛОВОГО ОБОРУДОВАНИЯ. ОСНОВЫ ТЕОРИИ НАДЕЖНОСТИ

Надежность — свойство изделий, характеризующее их работу во времени, т. е. оно учитывает изменения основных характеристик изделий, происходящие в процессе эксплуатации.

Основой надежности изделия является его качество — совокупность свойств, определяющих степень пригодности изделия для практического при­менения в соответствии с его назначением.

Понятие о качестве - изделия зависит от его назначения, техниче­ских требований, предъявляемых к этому изделию, и способа его использо­вания.

Для большей объективности оценки качества изделий надо стремиться к увеличению доли количественных показателей. В совокупность свойств, определяющих качество изделия, входят параметры, характеризующие изделие с различных точек зрения.,

Различают основные параметры — количественные показа­тели, характеризующие свойства изделия, наиболее важные для его функциони­рования (например, мощность, производительность, скорость, давление, грузо­подъемность), и второстепенные параметры — качественные показатели, характеризующие удобство работы, внешний вид и др.

Теория надежности занимается изучением закономерностей изменений свойств изделий, происходящих в процессе эксплуатации,.

Свойства, определяющие качество про­мышленных изделий, можно разделить на две группы:

1) так называемые «мгновенные свойства, которые могут быть оценены за короткий промежуток времени при контрольных проверках изделий на за­воде-изготовителе или в самом начале эксплуатации (мощность, производитель­ность, внешний вид и пр.);

2) свойства, требующие длительного наблюдения за работой изделия во время эксплуатации или при специальных испытаниях на надежность.

Основные термины в области надежности в технике регламентируются ГОСТ 13377-67.

Основные понятия и определения теории надежности с учетом указанного ГОСТ можно разбить на четыре группы.

ОБЪЕКТЫ

В эту группу входят изделия (системы) и детали (элементы системы), не­ремонтируемые и ремонтируемые.

Изделие — наиболее общее понятие об объектах. К изделиям относятся машины, механизмы, агрегаты, их элементы, которые являются предметом исследования или расчета надежности.

Изделия и детали—понятия относительные. Так, для завода, изготовляющего буровые насосы, поршни, цилиндровые втулки, клапаны являются деталями, а для заводов, производящих запасные части к буровым насосам — изделиями.

Неремонтируемыми называются такие изделия, которые в случае возник­новения отказа не подлежат или не поддаются ремонту. К неремонтируемым изделиям относятся многие детали бурового и нефтегазопромыслового обо­рудования. Отдельные части машин и механизмов, а также сами машины и ме­ханизмы в некоторых случаях можно рассматривать как неремонтируемые изделия. Например, большинство видов инструмента, в том числе породоразрушающий инструмент, также целесообразно рассматривать как неремонти­руемые изделия.

Ремонтируемыми называются такие изделия, которые можно ремонтиро­вать в случае возникновения отказа.

СОСТОЯНИЯ И СОБЫТИЯ

Работоспособность — состояние изделия, при котором оно способно вы­полнять заданные функции с параметрами, установленными требованиями технической -документации.

Неисправность — состояние изделия, при котором оно не соответствует хотя бы одному из требований технической документации. Следует различать неисправности, не приводящие к отказам, и неисправности (и их сочетания), вызывающие отказы.

Отказ — событие, заключающееся в нарушении работоспособности. Отказы можно классифицировать по различным признакам (табл. 1.1).

Условия возникновения отказа - возникший в нормальных и ненор­мальных условиях

По причинам возникновения отказы подразделя­ются на две группы: 1) отказы, не связанные с разрушением элементов системы и 2) отказы, обусловленные разрушением элементов. При этом под разрушением можно понимать не только поломки, но и случаи интенсивного изнашивания, как результат нарушения нормального режима работы (например, попадание абразива в смазку).

Основные виды отказов по происхождению можно характеризовать следующим образом:

конструкционный — отказ, вызванный недостатком конструкции;

технологический — отказ, возникающий в результате отклоне­ния от принятого технологического процесса изготовления изделия или в ре­зультате несовершенства этого процесса;

эксплуатационный— отказ, возникающий в результате нару­шения установленных правил эксплуатации или ремонта;

Характер проявления отказов характеризуется:

внезапный — отказ, сопровождающийся скачкообразным изменением одного или нескольких основных параметров изделия; а также постепенный, явный, скры­тый, полный и частичный отказ.

Взаимосвязь отказов- независимый и зависимый

Возможность прогнозирования заключается в том, что отказ может быть

не прогнозируемый — отказ, который заранее нельзя предвидеть;

прогнозируемый — отказ, который можно заранее предвидеть, например, по количеству проработанных изделием часов или по изменению одного или йескольких параметров изделия.

По сложности устранения- отказ простой и сложный

Отказы, при эксплуатации сложных систем возникают в случайные моменты времени. Поскольку отказы устраняются, то в течение времени наблюдается их поток. Под потоком отказов понимается последовательность отка­зов, происходящих один за другим в случайные моменты времени. Вид потока отказов определяет аналитические зависимости между количественными харак­теристиками надежности.

СВОЙСТВА

Надежность — свойство изделия выполнять заданные функции, сохраняя свои эксплуатационные показатели в заданных пределах в течение требуемого промежутка времени или требуемой наработки.

Безотказность — свойство изделия сохранять работоспособность в течение некоторой наработки без вынужденных перерывов.

Ремонтопригодность — свойство изделия, заключающееся в его приспо­собленности к предупреждению, обнаружению и устранению отказов и неис­правностей путем проведения технического обслуживания и ремонтов.

Сохраняемость — свойство изделия сохранять обусловленные эксплуата­ционные показатели в течение и после срока хранения и транспортирования, установленного в технической документации.

Долговечность — свойство изделия сохранять работоспособность до пре­дельного состояния с необходимыми перерывами для технического обслужи­вания и ремонтов. Предельное состояние — это такое состояние изделия, при достижении которого дальнейшая эксплуатация становится экономически нецелесообразной или опасной.

КОЛИЧЕСТВЕННЫЕ ПОКАЗАТЕЛИ НАДЕЖНОСТИ

Надежность машин и механизмов зависит от таких факторов, как характер и величина нагрузок, материал и конструкция сопряженных деталей, качество изготовления, условия эксплуатации и др. Воздействие значительной части этих факторов носит случайный характер (случайные перегрузки, дефекты в металле), вследствие чего возникающие отказы по своей природе являются случайными. В результате все величины, используемые при оценке надежности (время работы оборудования до первого отказа, время между последовательными отказами, число отказов за определенное время) также являются случайными. Поэтому основные закономерности, характеризующие надежность машин и механизмов, устанавливаются на основе статистических данных с применением законов теории вероятностей и математической статистики.     

 

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТ. СТАТИСТИКИ                                                       1

-Теория вероятностей — это наука о массовых случайных событиях, т. е.|, таких событиях, которые эквивалентны друг другу в отношении определенных свойств, или способны многократно повторяться при воспроизведении соответствующих условий. Теория вероятностей изучает свойства массовых случайных событий с использованием математических методов. Создают математическую модель изучаемых свойств, в которой они обозначаются математическими сим­волами, что позволяет оперировать этими свойствами как чисто математиче­скими понятиями. Основными исходными категориями теории вероятностей служат случайные явления и события.

Случайным называется такое явление, которое при неодно­кратном повторении одного и того же опыта каждый раз может протекать неодинаково, например: скорость проходки на разных буровых и действитель­ные размеры при измерениях.

Случайным событием называется качественный результат опы­тов, который может произойти или не произойти (отказ, безотказная работа).

Вероятностью случайного события называется сте­пень объективной возможности этого события, выраженная числом.

В качестве единицы измерения для вероятности принята вероятность достоверного события, которое непременно должно произойти в ре­зультате проведения опыта.

Противоположным по отношению к достоверному событию является не­возможное событие, которое в данном опыте произойти не может.

Математическая вероятность появления события А обозначается символом Р [А], характеризуемым случайной величиной.

Случайной величиной называется такая переменная величина, которая в результате опыта принимает одно из возможных заранее неизвест­ных значений. Случайная величина является количественной характеристикой случайного явления или события.

Случайные величины могут быть дискретными (прерывными) и непрерыв­ными. Так, количество отказов за некоторый промежуток времени характери­зуется дискретной случайной величиной, а значение времени безотказной ра­боты — непрерывной случайной величиной. Исчерпывающей характеристикой случайной величины является закон распределения, устанавливающий связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения случайной величины обычно задается функцией распределения.

Если x непрерывная случайная величина и х — произвольное действитель­ное число, то вероятность того, что x примет значение меньшее х, называется функцией распределения вероятностей случайной величины x,

Производная от функции распределения (если она существует), называется плотностью распределения случайной величины и является другой формой задания закона распределения случайной величины:

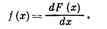
Для количественной оценки случайных величин используется математи­ческая статистика, с помощью которой получают так называемые оценки (под­ходящие значения) числовых характеристик искомой случайной величины (в том числе, и математической вероятности Р {А}).

Эти оценки называются статистическими и, в отличие от ве­роятностных (математических) обозначаются теми же симво­лами, но со звездочкой. Так, Р*{А}— есть статистическая вероятность события А.

Если произведена серия из п опытов, в каждом из которых могло появиться некоторое событие А, то вероятность этого события в данном опыте можно оце­нить по относительной доле благоприятных исходов.

Статистическую вероятность события А вычисляют как отношение числа благоприятных случаев т к общему числу случаев п:

Статистическую вероятность часто называют также относительной частотой или частостью появления события.

В теории надежности наиболее важными числовыми характеристиками случайных величин являются: математическое ожидание, дисперсия, среднее квадратичное отклонение и коэффициент вариации.

М а т е м а т и ч е с к о е ожидание случайной величины x харак­теризует некоторое число, около которого группируются возможные значения случайной величины:

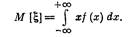
Дисперсией называется числовая характеристика, применяемая для оценки разброса значений случайной величины около ее среднего значе­ния. Дисперсия обозначается символом D [x] или s² [x] и определяется как математическое ожидание квадрата отклонений случайной величины от ее мате­матического ожидания

Средним квадратичным отклонением называется квад­ратный корень из дисперсии

Коэффициентом вариации случайной величины называется отношение

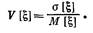
Для оценки математического ожидания случайной величины в качестве выборочной характеристики применяют среднее арифметическое:

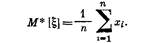
В качестве оценки дисперсии случайной величины (при п >= 30) исполь­зуется формула:

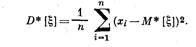
При ограниченном числе данных (при п < 30) следует пользоваться фор­мулой:

Случайные величины в зависимости от их физического смысла могут иметь различные законы распределения. Наиболее часто в теории надежности встре­чаются следующие законы распределения: нормальный, логарифмически нор­мальный, экспоненциальный, Вейбулла и гамма-распределение.

Рассмотрим основные теоретические и приближенные (статистические) уравнения для определения численных значений количественных показателей надежности.

Вероятность безотказной работы подразумевает, что в заданном интервале времени или в пределах заданной наработки не возникнет отказа изделия.

Пусть t — время работы изучаемого изделия и T — случайное время без­отказной работы, т. е. время, прошедшее с начала работы до первого отказа. Тогда событие Т > t означает, что в течение времени t не произойдет ни одного отказа изделия.

Для каждого значения t существует определенная вероятность того, что Т примет значение, большее t, т. е.

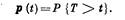
Функцию p (t) называют вероятностью безотказной работы. Функция р (t) является непрерывной функцией времени, обладающей следующими очевидными свойствами:

1) p(0) ⁼ 1) - т.е. в момент начала работы изделия исправны;

2) p (t) является монотонно убывающей функцией времени;

3) при t -> оо, р (t) -> 0.

Статистически вероятность безотказной работы характеризуется отноше­нием числа исправно работающих изделий к общему числу изделий, находя­щихся под наблюдением,

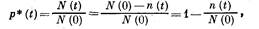
где N (0) — количество исправных изделий в момент времени t = 0; N (t) — количество исправных изделий в момент времени t; n (t) — количество отка­завших изделии к моменту времени t.

Если на основании статистических данных определено эмпирическое рас­пределение рассматриваемой случайной величины и установлена степень его близости к принятому теоретическому распределению, то вероятность безот­казной работы может быть рассчитана по известным математическим зависимо­стям. Так, если вероятность безотказной работы машины в течение 1000 ч составляет 0,95, то это означает, что в среднем около 5% машин данной модели потеряет свою работоспособность раньше, чем через 1000 ч работы.

Исправная работа и отказ — события противоположные.

Вероятность отказа — вероятность того, что в заданном интервале времени или в пределах заданной наработки возникнет отказ изделия:

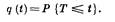
Из этого выражения видно, что вероятность отказа является функцией распределения случайного времени Т безотказной работы.

Статистическая оценка вероятности отказа — отношение числа изделий,, отказавших к моменту времени t, к числу изделий, исправных в начальный момент времени (т. е. при t = 0) — определяется по формуле:        ^\

Вероятность безотказной работы и вероятность отказа связаны зависимостью

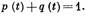
Частота отказов — это плотность вероятности того, что случайное время Т безотказной работы изделия окажется меньше времени t, или плотность вероят­ности отказа до момента времени t:

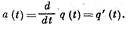
Статистическая оценка частоты отказов определяется как отношение числа отказавших изделий в единицу времени к первоначальному числу испытывае­мых или находящихся под наблюдением изделий (при условии, что отказавшие изделия не ремонтируются и не заменяются исправными):

где N (t + D t) — количество исправных изделий в момент времени (t + D t) Интенсивность отказов — вероятность отказа неремонтируемого изделия в единицу времени после данного момента времени при условии, что отказ до этого момента не возник. Иными словами, интенсивность отказов — это услов­ная плотность вероятности отказа изделия для момента времени t.

Статистическая оценка интенсивности отказов — это отношение числа отказавших изделий в единицу времени к среднему числу изделий, исправно работавших в рассматриваемый промежуток времени (при условии, что отка­завшие изделия не ремонтируются и не заменяются исправными, т. е. число испытываемых или находящихся под наблюдением изделий с течением времени уменьшается). Она определяется по формуле:

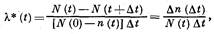
где А? — интервал времени; Аге (Л?) — количество отказавших изделий за время Д?.

Средняя наработка до первого отказа — это среднее значение наработки изделий в партии до первого отказа (для неремонтируемых изделий термин «средняя наработка до первого отказа» равнозначен термину «средняя нара­ботка до отказа»).

Если наработка выражена в единицах времени, можно применять термин «среднее время безотказной работы»:

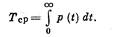
Статистическую оценку средней наработки до отказа (среднее арифмети­ческое наработок группы изделий до отказа) определяют по.формуле:

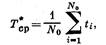
где Nо — количество испытываемых (находящихся под наблюдением) изде­лий; t_i — наработка i-го изделия до отказа.

Для определения меры рассеивания наработок группы изделий до первого отказа необходимо применять показатель среднеквадратичного отклонения наработки до первого отказа, статистиче­скую оценку которого рассчитывают по формуле:

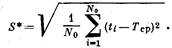
Наработка на отказ определяется как среднее значение наработки ре­монтируемого изделия многократного использования между отказами. Если наработка выражена в единицах времени, можно применять термин «среднее время безотказной работы»:

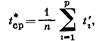
где п — количество отказов изделия в течение рассматриваемого периода эксплуатации; t _í ^' — время безотказной работы изделия между i -м. и (i + 1)-м отказами.

Для выявления меры рассеивания наработок на отказ необходимо приме­нять показатель среднее квадратичное отклонение на­работки на отказ, статистическую оценку которого определяют по формуле

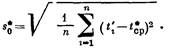
Параметр потока отказов — среднее количество отказов ремонтируемого изделия в единицу времени, взятое для рассматриваемого момента времени

где D n — количество однотипных деталей изделия, отказавших за время D t. Среднее время восстановления — среднее время вынужденного нерегла­ментированного простоя, вызванного отыскиванием и устранением одного отказа

Для определения меры рассеивания времени восстановления изделий необходимо применять показатель среднее квадратичное откло­нение времени восстановления, статистическая оценка ко­торого определяется по формуле

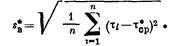
Среднее время восстановления — одна из наиболее наглядных количествен­ных характеристик, позволяющих оценивать ремонтопригодность изделий, рассчитанных на длительное использование.

Коэффициент готовности — вероятность того, что изделие будет работо­способно в произвольно выбранный момент времени в промежутках между выполнениями планового технического обслуживания.

Статистическая оценка коэффициента готовности определяется как отно­шение суммарного времени безотказной работы изделия за некоторый период эксплуатации к сумме времени безотказной работы и времени, затраченного на отыскание и устранение отказов за тот же период эксплуатации,

где t_i — время, затраченное на отыскание и устранение i-го отказа; t_ср — сред­нее время восстановления.

Коэффициент готовности характеризует обобщенные свойства обслужи­ваемого оборудования. Например, изделие с высокой интенсивностью отказов, но быстро восстанавливаемое, может иметь коэффициент готовности более высокий по сравнению с изделием с малой интенсивностью отказов и большим средним временем восстановления.

Коэффициент технического использования — отношение наработки изделия в единицах времени за некоторый период эксплуатации к сумме этой наработки и времени всех простоев, вызванных техническим обслуживанием и ремонтами за тот же период эксплуатации

где t_пр j — время, затраченное на j-и ремонт; k — количество технических обслуживании и ремонтов изделий в течение рассматриваемого периода эксплуатации.

Ресурс — наработка изделий до предельного состояния, оговоренного в технической документации. Различают ресурс до первого ре­монта, межремонтный ресурс, назначенный ресурс, средний ресурс и др.

Средняя продолжительность работы изделия за период эксплуатации до разрушения или другого предельного состояния называется средним ресурсом.

Статистическая оценка среднего ресурса определяется по формуле

где R_j — ресурс j-го изделия

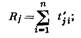
t_ji — время безотказной работы j-го изделия между i-м и (i + 1)-м отказами;

п — количество отказов изделия в течение рассматриваемого периода эксплуа­тации; Nо — количество испытываемых изделий.

Гамма-процентный ресурс R g — ресурс, который имеет и превышает в сред­нем обусловленное число (g) процентов изделий данного типа.

Срок службы — календарная продолжительность эксплуатации изделия до момента возникновения предельного состояния, оговоренного в техниче­ской документации, или до списания изделия.

Различают срок службы до первого капитального (среднего) ремонта, срок службы между капиталь­ными ремонтами, срок службы до списания, сред­ний срок службы и др.

Удельная трудоемкость ремонтов — отношение бредней трудоемкости ре­монтов к средней наработке изделия за один и тот же период '' эксплуатации

где Uср — средняя трудоемкость ремонтов.                  '

Коэффициент восстановления параметра — отношение значения параметра изделия после ремонта (или после устранения отказа) к номинальному значе­нию этого параметра                                        >

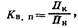
где Пк — обобщенный параметр изделия после ремонта или устранения от­каза; Пн — обобщенный параметр нового изделия.

Количественные показатели надежности бурового и нефтегазопромысло-вого оборудования следует включать в технические задания на проектирование, технические условия на изготовление, свидетельства на право серийного производства, карты технического уровня и технические паспорта изделий.

В техническую документацию следует включать только наиболее характер­ные для данного конкретного изделия показатели надежности, которые уста­навливают в зависимости от назначения изделия и условий его эксплуатации.

Достаточно полно надежность бурового и нефтегазопромыслового обору­дования характеризуется комплексом из четырех — пяти показателей, опре­деляющих безотказность, долговечность и ремонтопригодность.

Надежность ремонтируемых изделий обусловливается их безотказностью, долговечностью и ремонтопригодностью, а надежность неремонтируемых изде­лий—характеризуется в основном их безотказностью.

 Долговечность неремонтируемых изделий совпадает с периодом их без­отказной работы.

Поделиться:

Воспользуйтесь поиском по сайту: