Математика Древнего Египта

Цифры и числа

Египтяне пользовались непозиционной десятичной системой счисления. Выглядели цифры примерно так:

Эти цифры относятся к т.н. иероглифическому письму, которое позже было заменено иератическим. Я очень люблю иератическое письмо. Оно выглядит весьма стильно. Но здесь я буду использовать иероглифическое начертание.
Все целые числ образовывались путем повторения знаков, приведенных выше (и некоторых других для еще более высоких разрядов). Например, 3215 будет:

Очень ясная система, хотя не слишком лаконичная. Ее просто освоить, но числа получаются не слишком удобными. С первого взгляда трудно уловить точное значение числа. Писали египтяне в разных направлениях, но я здесь пишу как привычно нам слева на право.
Теперь насчет дробей. Для трех дробей существовали специальные значки:

Все остальные дроби, у которых в числителе была единица, обозначались знаменателем и похожим на глаз значком сверху. Например, ниже я написал 1/14

Все правильные дроби записывались как сумма таких дробей. Например:

На одном сайте я прочитал, что «в некоторых случаях» египетские дроби «лучше наших». И даже в английской вики, есть такой чудный пример: «Египетские дроби иногда легче позволяют сравнить размер дробей. Например, если некто хочет знать, больше ли 4/5, чем ¾ он может превратить их в египетские дроби:
4/5= 1/2 + 1/4+ 1/20
3/4= 1/2 +1/4»
Мне этот «легкий способ» напоминает шутку про Фейнмана, который ради какой-то задачи школьного курса просуммировал ряды в уме. Я гуманитарий и особо не умею считать, но сравнивать в уме обычные дроби в их нормальной записи мне кажется гораздо проще, чем переводить их в египетский вид. Возможно, для египтян сравнения такого рода и были более удобны, так как наших дробей они не знали.

Сложение и умножение

Ну, вот мы и переходим к главному. Как египтяне считали? Сложение и вычитание целых чисел у них происходило также как и у нас, а может быть даже проще, им ведь просто нужно было объединить иероглифы и учесть смену разрядов. А как обстоит дело с умножением и делением? В древнеегипетском мире это была вовсе не тривиальная задача.
Египтяне использовали такой алгоритм для умножения. В два столбца писались числа. Первый столбец начинался с единицы, а второй с множимого. Затем каждое число в столбце удваивалось до тех пор, пока из некоторых чисел первого столбца не удастся сложить множитель. Вы поняли? На примере понятно лучше. Например, 7 на 22

8 уже больше, чем 7, поэтому табличка заканчивается на четырех. Теперь 1+2+4=7 значит 22+44+88=154. Хотите верьте, хотите нет но 154 это верный ответ. Конечно в египетской записи (я не знаю, как она точно выглядела) такие вычисления были проще, ведь умножать на 2 в египетской записи очень просто.
Еще пример, немного сложнее: 13 умножить на 57

1*
4*
8*

1+4+8=13 и 57+228+456=741
Иногда, чтобы ускорить процесс прибегали к умножению на 10.
Может возникнуть вопрос, всегда ли можно представить множитель в таком виде? Да, на самом деле мы фактически имеем дело с двоичной системой счисления: 1*2⁰+0*2¹+1*2²+1*2³ т.е. 1+100+ 1000=1101
Деление выполнялось при помощи схожего алгоритма. Разделим 238 на 17:
Опять составляем табличку с одной стороны, которой стоит 17 с другой единица. Процесс удвоения останавливается на числе, которое при удвоении будет больше делимого.

Здесь нужно составить число 238 из чисел второго столбца, начиная с конца. 136+68+34=238, значит нам нужны числа 8+4+2=14. Итак, 238/17 =14
К несчастью, деление не всегда приводит к целому числу. В ряде случаев это было довольно сложно. Я покажу простой пример, заимствованный мной из одной книги.
Разделим 213 на 8
Сначала все, как обычно.

2*
8*
16*

Здесь мы останавливемся, ведь 128 на 2 = 256, а это больше 213. 128+64<213. 128+64+32 уже опять больше. Не подходит. 128+64+16<213 Пока все ОК. 128+64+16+8 уже больше. Значит мы смогли набрать только 208=128+64+16 из 213. И нам осталось разделить 213-208=5
Мы делим делитель по полам, используя уже привычную таблицу. К счастью 5 это 1+4.

1/2*
1/4
1/8*

Таким образом, окончательный результат будет
213/8 = 2+8+16+1/2+1/8 =26+1/2+1/8
Сейчас мы имеем удачный случай, но так получается не всегда.

Математика Древнего Египта

Мы начнем наше исследование гораздо раньше указанных дат в описании проекта. Ведь успехи античных математиков (в том числе и Фалеса) не могли возникнуть на пустом месте. Народы Древнего востока на протяжении многих веков сделали немало открытий в арифметике, геометрии и астрономии.

Самые ранние математические тексты, известные в наши дни, оставили две великие цивилизации древности - Египет и Месопотамия. Именно там появились первые математические задачи, решения которых требовала повседневная жизнь.

Уровень древнеегипетской математики был довольно высок. Источников, по которым можно судить об уровне математических знаний древних египтян, совсем немного. Во-первых, это папирус Райнда, названный так по имени своего первого владельца. Он был найден в 1858 г., расшифрован и издан в 1870 г. Рукопись представляла собой узкую (33 см) и длинную (5,25 м) полосу папируса, содержащую 84 задачи. Теперь одна часть папируса хранится в Британском музее в Лондоне, а другая находится в Нью-Йорке. Во-вторых, так называемый Московский папирус - его в декабре 1888 г. приобрёл в Луксоре русский Египтолог Владимир Семёнович Голенищев. Сейчас папирус принадлежит Государственному музею изобразительных искусств имени А. С. Пушкина. Этот свиток длиной 5,44 м и шириной 8 см включает 25 задач. И наконец, "Кожаный свиток египетской математики", с большим трудом расправлённый в 1927 г. и во многом проливший свет на арифметические знания египтян. Ныне он хранится в Британском музее. Подобные папирусы, по-видимому, служили своего рода учебниками. В папирусах есть задачи на вычисление - образцы выполнения арифметических операций, задачи на раздел имущества, на нахождение объёма амбара или корзины, площади поля и т. д.

Все правила счёта древних египтян основывались на умении складывать и вычитать, удваивать числа и дополнять дроби до единицы. Умножение и деление сводили к сложению при помощи особой операции - многократного удвоения или раздвоения чисел. Выглядели такие расчёты довольно громоздко. Для дробей были специальные обозначения. Египтяне использовали дроби вида 1/n, где n - натуральное число. Такие дроби называются аликвотными. Иногда вместо деления m:n производили умножение m*(1/n). Надо сказать, что действия с дробями составляли особенность египетской арифметики, в которой самые простые вычисления порой превращались в сложные задачи.

Сравнительно небольшой круг задач в египетских папирусах сводится к решению простейших уравнений с одним неизвестным. При решении подобных задач для неизвестного использовали специальный иероглиф со значением "куча". В задачах про "кучу", решаемых единым методом, можно усмотреть зачатки алгебры как науки об уравнениях.

В египетских папирусах встречаются также задачи на арифметическую и геометрическую прогрессии, что ещё раз подчёркивает не только практический, но и теоретический характер древней математики. Поразительно, но при довольно примитивной и громоздкой арифметике египтяне смогли добиться значительных успехов в геометрии. Они умели точно находить площадь поля прямоугольной, треугольной и трапециевидной формы. Известно, что в середине І тысячелетия до н. э. для построения прямого угла египтяне использовали верёвку, разделённую узлами на 12 равных частей. Концы верёвки связывали и затем натягивали её на 3 колышка. Если стороны относились как 3:4:5, то получался прямоугольный треугольник. И это - единственный прямоугольный треугольник, который знали в Древнем Египте.

Важным достижением геометрической науки египтян было очень хорошее приближение числа π, которое получается из формулы для площади круга диаметра d. Этому правилу из 50-ой задачи папируса Райанда соответствует значение π»3,1605. Однако каким образом египтяне получили саму формулу, из контекста неясно. Заметим, что на всём Древнем Востоке при вычислениях использовалось значение π=3. Так что в этом отношении египтяне намного опередили другие народы.

Среди пространственных тел самым "египетским" можно считать пирамиду, ведь именно такую форму имеют знаменитые усыпальницы фараонов. Так вот, оказывается, кроме объёма куба, параллелепипеда, призмы и цилиндра египтяне умели вычислять объём усечённой пирамиды, в основаниях которой лежат квадраты со сторонами a и b, а высота h. Для этого они применяли специальную формулу. Эта формула считается высшим достижением древнеегипетской математики.

Математика в Древнем Египте представляла собой совокупность знаний, между которыми ещё не существовало чётких границ. Это были правила для решения конкретных задач, имевших практическое значение. И лишь постепенно, очень и очень медленно, задачи начали обобщаться и приобретать более абстрактные черты.

Как могло появиться первое приближение числа π

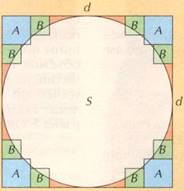
По поводу формулы площади круга нам кажется весьма правдоподобной гипотеза автора многочисленных книг по истории математика А.Е. Раик: площадь круга диаметра d сравнивается с площадью описанного вокруг него квадрата, из которого по очереди удаляются малые квадраты со сторонами (1/6)d и (1/9)d.

В наших обозначениях вычисления будут выглядеть так. В первом приближении площади круга S равна разности между площадью квадрата со стороной d и суммарной площадью 4-ёх малых квадратов А со стороной (1/6)d:

S»d²-4(1/6*d)²=d²(1-1/9)=(8/9)d²

Далее из полученной площади нужно вычесть площадь 8-ми квадратов В со стороной (1/9)d, и тогда площадь круга будет приближённо равна следующему выражению:

S»(1-1/9)d²-8(1/9*d)²=(1-1/9)d²-1/9*(8/9)d²=(1-1/9)d²-1/9(1-1/9)d²=(1-1/9)²d²

 

Как зародилась математика в Древнем Египте?

Использовалась математика Древнего Египта также при строительстве дамб, плотин, каналов. Труды многих ученых по установлению порядка чисел не сохранились по двум причинам:

1. Папирус — плохой носитель информации, так как сохранял ее: записи выцветали, сам папирус быстро ветшал, а копий работ, естественно не было.

2. Математики этой страны относились к письменному оформлению своих открытий и решений практических задач не настолько серьезно, как их древнегреческие коллеги. Многие математические задачи, свойства чисел и геометрических фигур передавались в устной форме. Они не преследовали цель накопления, обобщения и сохранение математических знаний. Для них было самым важным практическое применение математической науки на благо человека. Поэтому сегодня математика Древнего Египта для нас часто ограничивается всем известным понятием «египетский треугольник».

Эти две причины объясняют, почему знания о математике и математиках Древнего Египта сохранились до наших дней плохо, хотя можно сказать более категорично, что очень плохо. А математики Древней Греции с усердием и настойчиво учились у исследователей Египта. Они старательно изучали все их папирусные рукописи по математике. Этот факт в истории математике не раскрыт детально. Подробности развития математики в стране фараонов е начинают описывать историки времен воцарения в Древней Греции Птоломеев. В это время начинается бурное и плодотворное объединение египетской и греческой культур.

Значительные математические труды древних египетских математиков

В Древнем Египте (с 2040 по 1078 годы до н.э) были написаны следующие труды древнеегипетских
математиков:

1. Папирус Ахмеса (известного еще как папирус Ринда). В настоящее время его первая часть хранится в Британском музее (Лондон), вторая в Нью-Йорке Манускрипт, содержащий 84 задачи. Из этого сборника задача человечество узнало о том, что математика в Древнем Египтедостигла высокого уровня и древнеегипетские математики умели:

· находить квадратный корень;

· возводить в степень.

· решали уравнения с одним неизвестным первой и второй степени;

· в одной из задач речь идет о прогрессиях;

· очень много задач в этой работе посвящено нахождению площади треугольника, квадрата, круга.

Все задачи имели практический характер и относились к строительству, размежеванию земельных наделов.

Практически все найденные рукописи, свидетельствовали о том, что математика Древнего Египта имела практическую направленность своих задач.

2. Московский папирус содержит намного меньше задач (всего 25) по сравнению с манускриптом Ахмеса. Однако он на 200 лет старше его. Первый владелец его — известный русский египтолог В.С. Голенищев. Практически все приведенные в этом труде задачи посвящены геометрии.

3. Менее значимые в плане количества рассматриваемых задач были Берлинский папирус — «кожаный свиток», папирусы из Лахуна, папирус Рейснера. В этих работах математические задачи перемежевывались с вопросами медицины.

Вклад ученых Древнего Египта в развитие науки

Очень интересной познавательной работой может стать математика Древнего Египта в презентациях, которая раскроет детально вклад египетских математиков в развитие этой науки.

Самыми значительными открытиями в области математики у древних египтян можно считать:

1. Нумерация чисел. Она была похожа на римскую арефметику. В ней использовались числа, кратные 10. Потом появились значки, обозначающие цифры от 1 до 9.

2. Умножение чисел. Это действие египтяне выполняли с помощью сочетания сложения и удвоения чисел.

3. Решение уравнений.

4. Постановка и решение задач на площади плоских фигур.

5. Решение задач на вычисление объемов различных стереометрических фигур.

6. Введение значков сложения и вычитания чисел.

Следует заметить, что всем, кто захочет написать такой большой труд, как математика Древнего Египта в реферате, может найти обширную информацию в научно-популярных изданиях.

В Египте математика использовалась еще с самых древних времен, что подтверждается различными текстами, которые относятся к началу второго тысячелетия до н.э. Применялась математика в Древнем Египте очень часто и в основном в таких направлениях, как мореплавание, астрономия, строительство и землемерие. Но, что удивительно при таком распространении счета, денег и, соответственно, денежных расчетов в те времена у египтян не было. К огромному сожалению, у современного человека очень мало сведений о древнеегипетской математике, так как все записи египтяне делали на папирусе, а он очень плохо сохраняется. Но даже по тому количеству дошедших до нашего времени документов и записей можно с полной уверенностью сказать, что геометрия и арифметика в Древнем Египте была развита весьма неплохо. И стоит отметить, что ученые Греции и Вавилона учились у египтян математике.

Поделиться:

Воспользуйтесь поиском по сайту: