 |
б) на арифметическую прогрессию.
|
|
|
|
Лекция 3
Тема: Математика Древнего Египта.
:
1. Источники (Московский папирус, папирус Райнда).
2. Иероглифическая нумерация.
3. Действие над натуральными числами и дробями.
4. Красные числа.
5. Задачи, приводящие к линейным и двучленным квадратным уравнениям.
6. Прогрессии.
7. Геометрические знания.
8. Значение математики древнего Египта.
1. Наиболее древние письменные математические тексты, известные в настоящее время, принадлежат таким великим цивилизациям древнего Востока как ЕгипетиВавилон, возникших в долинах Нила, Двуречья Тигра и Евфрата. Одновременно с древним Египтом и Вавилоном появились цивилизации в Индии, в Китае, Средней Азии и Закавказье, Индокитае и Индонезии, на островах и европейском и азиатском побережье Средиземного моря. Математические документы сохранились только в Египте, Месопотамии, Индии и Китае. Все эти государства были земледельческими.
Площадь, пригодная для земледелия во всех этих странах была невелика, её можно было увеличить только путём проведения оросительных каналов или осушения болот. Работы по проведению каналов и осушению болот, необходимость установления границ между полями потребовали создания сельских общин. Поэтому наряду с натуральным хозяйством этих общин появляется распределение, связанное со значительными общественными работами, а также с частыми войнами, в которые вовлекаются большие массы людей.
В этих государствах появляются математические задачи, к которым приводит необходимость расчётов при проведении каналов, строительстве плотин, складов для зерна, дворцов, храмов и военных укреплений, при межевании земель, распределении материалов и продуктов среди участников общественных работ или военных походов, при торговых сделках, вождении торговых или военных караванов и мореплавании. Об этих задачах и говорят те математические документы, которые в том или ином виде сохранились до нашего времени. В Египте математические тексты писались на хрупком папирусе, иногда на коже, и сохранились только те тексты, которые были положены в пирамиды – усыпальницы высокопоставленных египтян – для того, чтобы души покойников могли читать свои любимые произведения в загробном мире; вавилонские же тексты были написаны клинописью на сырой глине, которая затем обжигалась, и до нас дошло огромное число математических клинописных текстов.
|
|
|
Рассмотрим математику древнего Египта, о которой располагаем более бедными сведениями, по сравнению с Вавилоном.
Большинство математических текстов, сохранившихся в памятниках древнего Египта, написаны на папирусе – бумаге, выделанной из стебля одноимённого растения.
Самый большой, сохранившийся до наших дней древнеегипетский математический текст – это так называемый папирус Райнда размером (5,25м.  33см.), содержащий 84 задачи. Названный по имени владельца, приобретшего папирус в 1858 г., он ныне хранится частично в Лондонском Британском музее, частично в Нью-Йорке. Другой папирус примерно такой же длины, но гораздо более узкий (5,44м.
33см.), содержащий 84 задачи. Названный по имени владельца, приобретшего папирус в 1858 г., он ныне хранится частично в Лондонском Британском музее, частично в Нью-Йорке. Другой папирус примерно такой же длины, но гораздо более узкий (5,44м.  8см.), приобретённый в конце прошлого века русским востоковедом В.С. Голенищевым, принадлежит Московскому Музею изобразительных искусств имени А.С. Пушкина. Этот свиток содержит 25 задач. Оба папируса переведены на современные языки и прокомментированы и относятся папирусы к эпохе Среднего царства. Носителями научных знаний были чиновники, состоявшие на государственной или храмовой службе. Мы не располагаем никакими известиями о математических знаниях Раннего и Древнего царств, эпохи Нового царства. Правда полагают, судя по некоторым отрывкам, что математика мало изменилась с тех пор, как были составлены Московский папирус и папирус Райнда.
8см.), приобретённый в конце прошлого века русским востоковедом В.С. Голенищевым, принадлежит Московскому Музею изобразительных искусств имени А.С. Пушкина. Этот свиток содержит 25 задач. Оба папируса переведены на современные языки и прокомментированы и относятся папирусы к эпохе Среднего царства. Носителями научных знаний были чиновники, состоявшие на государственной или храмовой службе. Мы не располагаем никакими известиями о математических знаниях Раннего и Древнего царств, эпохи Нового царства. Правда полагают, судя по некоторым отрывкам, что математика мало изменилась с тех пор, как были составлены Московский папирус и папирус Райнда.
|
|
|
Дальнейшая история Египта, история 1 тысячелетия до нашей эры, - полоса упадка страны и господства иностранных завоевателей, сначала эфиопов, затем ассирийцев и персов. После завоеваний Египта Александром Македонским начинается процесс плодотворного синтеза греческой и египетской культур. Александрия становится крупнейшим центром науки наступающей эпохи эллинизма, и она сохраняет это значение еще долгие века спустя после завоевания Египта Римом (30 г. до н.э).
Вновь с математическими работами египтян мы встречаемся в эпоху эллинизма и в период распространения ислама, но это уже совсем другая культура, другая и математика. Древне египетская цивилизация закончила своё существование.
 2. Египетская иероглифическая нумерация была чисто аддитивной: имелись особые знаки только для единицы, десяти, ста, тысячи, десяти и ста тысяч, миллиона и десяти миллионов.
2. Египетская иероглифическая нумерация была чисто аддитивной: имелись особые знаки только для единицы, десяти, ста, тысячи, десяти и ста тысяч, миллиона и десяти миллионов.
При записи числа иероглифы единицы, десятка, сотни и т.д. писались столько раз, сколько в данном числе единиц в соответствующих разрядах, причем разряды записывались в порядке, обратном нашему (египтяне писали справа налево).
Например, число 624 писали так:
 |
Уже в скорописном иератическом письме, заменившем первоначальное иероглифическое письмо, которым и написаны дошедшие до нас математические папирусы, имеются особые знаки как для первых девяти чисел, так и для десятков, сотен и тысяч.
 Кроме обозначений целых чисел, египтяне имели также специальные обозначения для дробей вида
Кроме обозначений целых чисел, египтяне имели также специальные обозначения для дробей вида  и дроби
и дроби  ; дроби
; дроби 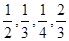 обозначались специальными иероглифами, а основные дроби вида
обозначались специальными иероглифами, а основные дроби вида  обозначались знаком числа n, над которым ставился знак
обозначались знаком числа n, над которым ставился знак  (рот- “часть”):
(рот- “часть”):  .
.
3. Счет у египтян состоял из умения складывать, удваивать, дополнять дроби до единицы. Поэтому умножение на целое число и деление без остатка производились с помощью удвоения, т.е. однократного сложения числа с самим собой. Для этого множитель представляли как сумму тех или иных членов последовательности 1,2,4,8,16,…, что всегда возможно. Рассмотрим схему умножения  из задачи №32 папируса Райнда, где множитель представлен в виде степеней двойки (колонка слева):
из задачи №32 папируса Райнда, где множитель представлен в виде степеней двойки (колонка слева):
|
|
|
1 12 на этом процесс удвоения заканчивается, т.к. среди
2 24 степеней двойки есть уже необходимые слагаемые
/4 48 множителя, которые отмечались косой чертой.
/8 96
Сумма 144
Особо выделялись еще умножение на 10 и 5, т.е. учитывались свойства десятичной системы.
Деление производилось как действие, обратное умножению. В задаче №69 папируса Райнда, где делится  , указание гласит: “Умножай 80 (буквально: складывай, начиная с 80), пока не получишь 1120”
, указание гласит: “Умножай 80 (буквально: складывай, начиная с 80), пока не получишь 1120”
1 80
/10 800
2 160
/4 320
________
1120.
Таким образом, непосредственно определяется сколько раз делитель содержится в делимом. Частное складывается из чисел, соответствующих слагаемым делителя, отмеченным черточкой.
Наряду с удвоением при делении употреблялось раздвоение. Например, для вычисления 2:8 пользовались схемой:



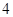
/ 

Деление целого числа на целое
1) 19:8.
Составим таблицу
 1 8
1 8
/2 16
 4
4
/  2
2
 1
1
В которой удвоение совершается один раз, т.к. следующее дало бы число, больше делимого.
Затем совершается деление пополам, продолжающееся до тех пор, пока справа не получится 1. Целая часть (2) находится так: вычитая из делимого (19) «частное произведение» (16), находим 3, это число нужно аддитивно составить из чисел правого столбца, т.к. последний содержит только степени числа 2, то это возможно единственным способом: 3=2+1. Отмечая соответствующие строки косыми чёрточками, находим, что частное выражается «смешанным числом»  или
или  , тогда
, тогда  . Так как в общем при делении целых чисел ответ не всегда будет однозначным. Например, результат деления 5:12 можно представить двояко:
. Так как в общем при делении целых чисел ответ не всегда будет однозначным. Например, результат деления 5:12 можно представить двояко:  и
и  , смотря по тому, как разбить число 5 на слагаемые, являющиеся делителем числа 12, т.е. представить ли его в виде 5=4+1 или 5=3+2. Кроме того, как правило, такое разбиение и не всегда возможно. Поэтому непосредственный подбор основных дробей, составляющих результат, в общем случае был очень трудным делом. Отсюда, вероятно, возникла идея составления подсобных таблиц, в которых содержались бы готовые результаты некоторых «опорных» операций.
, смотря по тому, как разбить число 5 на слагаемые, являющиеся делителем числа 12, т.е. представить ли его в виде 5=4+1 или 5=3+2. Кроме того, как правило, такое разбиение и не всегда возможно. Поэтому непосредственный подбор основных дробей, составляющих результат, в общем случае был очень трудным делом. Отсюда, вероятно, возникла идея составления подсобных таблиц, в которых содержались бы готовые результаты некоторых «опорных» операций.
Такой опорной операцией в египетской вычислительной технике служит деление 2: k, где k – нечетные целые числа (если k есть четное число 2 k/, то результат сразу представляется основной дробью  /). В самом деле, каждое целое число представляется с помощью последовательных удвоений (начиная от 1) в виде суммы степеней числа 2. Таким образом, вопрос о делении произвольного числа сводится к вопросу о делении чисел вида
/). В самом деле, каждое целое число представляется с помощью последовательных удвоений (начиная от 1) в виде суммы степеней числа 2. Таким образом, вопрос о делении произвольного числа сводится к вопросу о делении чисел вида  , например
, например  .
.
|
|
|
Источниками возникновения дробей послужили: 1) процесс дробления целого на части; 2) процесс измерения.
Самым трудным был случай нецелого деления. Общими рациональными дробями вида 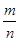 египтяне не оперировали. Это не значит, что они не имели вообще представления о таких дробях, они умели по-своему выражать частные вида m:n. Для этого им служили аликвотные дроби-доли единицы вида
египтяне не оперировали. Это не значит, что они не имели вообще представления о таких дробях, они умели по-своему выражать частные вида m:n. Для этого им служили аликвотные дроби-доли единицы вида  , которые принято записывать в виде
, которые принято записывать в виде  (у историков математики), черточка
(у историков математики), черточка  символизирует египетский знак. Деление m:n египтяне иногда представляли как умножение
символизирует египетский знак. Деление m:n египтяне иногда представляли как умножение  ; в этом, быть может, сказалось влияние математики вавилонян, которые всегда приводили деление на целое число к умножению на обратную ему дробь.
; в этом, быть может, сказалось влияние математики вавилонян, которые всегда приводили деление на целое число к умножению на обратную ему дробь.
 Кроме дробей вида
Кроме дробей вида  , египтяне оперировали еще дробью
, египтяне оперировали еще дробью  , для которой имелся знак, мы будем обозначать её
, для которой имелся знак, мы будем обозначать её  .
.
Дроби типа 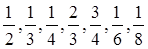 - натуральные дроби, имели индивидуальные названия (это были доли египетской единицы площади “сетат”).
- натуральные дроби, имели индивидуальные названия (это были доли египетской единицы площади “сетат”).
В вычислительной технике древнего Египта появилась теоретико-числовая задача о разложении дробей на сумму аликвотных. Эта задача, не имеющая единственного решения решалась египтянами эмпирически в несколько этапов.
Самые простые разложения чиновники должны были знать наизусть, они встречались на каждом шагу. В текстах они употребляются без особых разъяснений:
 |
Из них простыми комбинациями выводились следующие соотношения:
 , (3)
, (3)
 , (4)
, (4)
 . (5)
. (5)
Выражения (1) - (5) делятся на 2, 3, 4 и получается еще серия разложений:

 и т.п.
и т.п.
Правило (3) представляет начало создания таблицы канонических разложений при удвоении дробей:
 (то же, что (3)),
(то же, что (3)),
 (разделено на 3),
(разделено на 3),
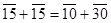 (разделено на 5) и т.п.
(разделено на 5) и т.п.
В таблице должны содержаться разложения только для нечетных  , т. к при удвоении дроби
, т. к при удвоении дроби  она дает просто
она дает просто 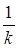 . При удвоении дробей вида
. При удвоении дробей вида  , можно пользоваться разложением
, можно пользоваться разложением
 .
.
4. Красные числа.
Красные числа это не что иное как дополнительные множители, подобные тем, которыми мы пользуемся при приведении дробей к общему знаменателю. Красные числа могут быть не только целыми, но и дробными. Общим знаменателем является не наименьшее общее кратное, а просто в большинстве случаев наибольший из знаменателей данных дробей. Все остальные дроби выражаются через эту наименьшую дробь, “измеряются” некоторой минимальной мерой, которая не всегда может целое число раз уложиться в заданных величинах. Эта процедура нужна была в тех сложных случаях деления 2 на 31, …, когда по египетскому способу, получив единицу с некоторой дробью, требовалось оценить, сколько же еще не хватает до 2.
|
|
|
Пример. Схема деления 37 на  в задаче 33 папируса Райнда такова:
в задаче 33 папируса Райнда такова:
1  .
.
2  (т.к.
(т.к. 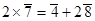 ).
).
4  (т.к.
(т.к.  ).
).
8 
16 
 Найти надо, сколько не достает дроби
Найти надо, сколько не достает дроби  до единицы и выразить в других единицах эту недостачу и делитель чтобы можно было сравнить их. Здесь такой единицей является дробь
до единицы и выразить в других единицах эту недостачу и делитель чтобы можно было сравнить их. Здесь такой единицей является дробь  а не
а не  , потому что главная цель красных чисел – дать в сумме целое число. Остаток в новых единицах, т.е. долях
, потому что главная цель красных чисел – дать в сумме целое число. Остаток в новых единицах, т.е. долях  :
:
Красные числа (они взяты в кружки)
 в сумме дают 40.
в сумме дают 40.
Значит до единицы не хватает двух  .
.
Делитель же в новых единицах
 |
слагается из:
т.е. равен 97 этих новых единиц. Следственно, в первой схеме удвоений к частному 16 надо еще прибавить  , что по таблице канонических разложений представляется суммой
, что по таблице канонических разложений представляется суммой 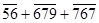 . Тогда в правой части схемы будет число 37, которому в левой части будет соответствовать частное, равное
. Тогда в правой части схемы будет число 37, которому в левой части будет соответствовать частное, равное  . Это и есть ответ.
. Это и есть ответ.
5. В задачах на “axa”, с современной точки зрения, решаются уравнения первой степени вида  , откуда
, откуда  .
.
Эта задача соответствует нашим линейным уравнениям с одним неизвестным. Слово “axa” означает “кучу”, “груду” (в смысле количества), и, конечно это количество есть неизвестная, которую надо найти.
Задача № 26 в папирусе Райнда. “Количество и его четвертая часть дают вместе 15” (мы бы записали:  ), а решение начинается словами: “Считай с 4;от них ты должен взять четверть, имеют 1, вместе 5”. После этого вычисляется
), а решение начинается словами: “Считай с 4;от них ты должен взять четверть, имеют 1, вместе 5”. После этого вычисляется  и
и  . Это следует понимать так. Вычислитель принимает, что количество есть 4, тогда прибавление четверти количества дает 5, а должно быть второе больше (
. Это следует понимать так. Вычислитель принимает, что количество есть 4, тогда прибавление четверти количества дает 5, а должно быть второе больше ( ); поэтому искомое количество также должно быть втрое больше принятого (
); поэтому искомое количество также должно быть втрое больше принятого ( ). Вообще, если «ложное положение» есть
). Вообще, если «ложное положение» есть  и оно дает
и оно дает  вместо
вместо  , то:
, то:
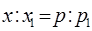 ,
,  .
.
С помощью метода ложного положения египтяне решали также задачи, которые можно выразить двучленным квадратным уравнением  . Такова, например задача №6 Московского папируса, в условии которой сообщается, что
. Такова, например задача №6 Московского папируса, в условии которой сообщается, что 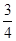 длины являются шириной, а площадь равна 12 и требуется определить стороны прямоугольника. Судя по порядку действий, решение основано на пропорциональной зависимости между квадратом предположенного значения длины, равной 1, и площадью, равной в таком случае
длины являются шириной, а площадь равна 12 и требуется определить стороны прямоугольника. Судя по порядку действий, решение основано на пропорциональной зависимости между квадратом предположенного значения длины, равной 1, и площадью, равной в таком случае 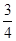 , а также квадратом истинной длины x и истинной заданной площадью 12:
, а также квадратом истинной длины x и истинной заданной площадью 12:
 .
.
В египетском решении прежде всего вычисляется  . Далее находится произведение
. Далее находится произведение 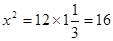 и
и  . Наконец, ширина есть
. Наконец, ширина есть  . Однако, имеются и другие истолкования этого решения.
. Однако, имеются и другие истолкования этого решения.
В группе задач на «аха», первых в истории математики отвлеченных задачах, решенных единым методом, видим зачатки алгебры как науки о решении уравнений.
«Квадрат и другой квадрат, сторона которого есть 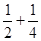 , стороны первого квадрата, имеют вместе площадь 100. Вычисли мне это».
, стороны первого квадрата, имеют вместе площадь 100. Вычисли мне это».
Решение. Возьми квадрат со стороной 1, и возьми 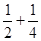 от 1, т.е.
от 1, т.е. 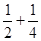 в качестве стороны второго квадрата. Умножь
в качестве стороны второго квадрата. Умножь 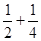 на самого себя; это дает
на самого себя; это дает  . Поскольку сторона первой площади взята за 1, а второй за
. Поскольку сторона первой площади взята за 1, а второй за 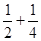 , то сложи обе площади вместе, это даст
, то сложи обе площади вместе, это даст  . Возьми отсюда корень: это будет
. Возьми отсюда корень: это будет 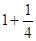 . Возьми корень из данных 100, это будет 10. Сколько раз входит
. Возьми корень из данных 100, это будет 10. Сколько раз входит 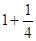 в 10? Это входит 8 раз (далее текст прочесть нельзя).
в 10? Это входит 8 раз (далее текст прочесть нельзя).
Задание студентам: объяснить решение задачи и восстановить содержание недостающей части текста.
Пояснения.
1. Применяются только дроби вида  , где
, где  и
и  . Применяются дроби
. Применяются дроби  и
и 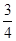 ,
, 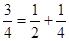 .
.
2. Применяется метод «ложного положения».
3. Деление рассматриваются как действие, обратное умножению, а последнее сводится к последовательным удвоениям.
Объяснение задачи.
Если сторона первого квадрата равна 1 «ложное положение», то сторона второго равна 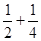 . Сумма площадей
. Сумма площадей  (т.е.
(т.е.  ). Корень квадратный из этого числа
). Корень квадратный из этого числа 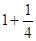 (т.е.
(т.е.  ). 8 раз содержится в 10, квадратном корне из 100. Деление
). 8 раз содержится в 10, квадратном корне из 100. Деление  производится как действие, обратное умножению, а последнее сводится к последовательным удвоениям. Троекратное удвоение
производится как действие, обратное умножению, а последнее сводится к последовательным удвоениям. Троекратное удвоение 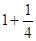 дает
дает  ; 5; 10, т.к. квадратный корень из числа
; 5; 10, т.к. квадратный корень из числа  в восемь раз меньше квадратного корня из 100, то принятое за длину стороны квадрата число, т.е. единицу, следует умножить на 8. Таким образом, легко восстанавливается содержание недостающей части текста: стороны искомых квадратов будут
в восемь раз меньше квадратного корня из 100, то принятое за длину стороны квадрата число, т.е. единицу, следует умножить на 8. Таким образом, легко восстанавливается содержание недостающей части текста: стороны искомых квадратов будут  и
и  .
.
6. Математические знания позволяли египетскому чиновнику производить расчеты при строительных работах, сборе налогов, разделе имущества, обмене и распределении продуктов, измерении площадей и объемов, плотин и зернохранилищ, переводе мер веса или емкости в другие единицы и т.п. Основное внимание в египетских текстах сконцентрировано не на методах решения задач, а на самих вычислениях.
Некоторая систематизация материала встречается в папирусе Райнда. Классификация задач производилась не по методам (например, задачи на пропорции, линейные уравнения и т.д.), а по темам. Задачи на припек можно объединить в один класс, задачи о ёмкости зернохранилищ и сосудов – в другой и т.д. Таким образом, каждая задача решается заново, без каких-либо пояснений в числах. Однако при решении вычислитель пользуется некоторыми общими законами. Так, решение первой группы задач основано на пропорциональной зависимости, второй – на формулах объема тел и т.д.
Для тренировки учащихся составлялись задачи развлекательного характера, не имевшие прямого практического применения, либо только имевшие вид практических. Наиболее яркой из них была задача на геометрическую прогрессию, - замечательная своей историей ”задача-путешественница”. В дальнейшем она с небольшими модификациями не раз встречалась в разные эпохи и у разных народов:
«Лестница дом 7
Кошка 49 1 2801
Мышь 343 2 5602
Ячмень 2401 4 11204
Мера 16807 вместе 19607».
В задаче речь идет о семи кошках в каждом из семи домов, каждая кошка съела по семь мышей, каждая из которых съела по семь колосьев ячменя; каждый же колос мог дать семь мер хлеба. Сумма домов, кошек, мышей, колосьев и мер хлеба находится путем умножения:
 .
.
Существует несколько гипотез о том, как именно было получено данное решение. Согласно О.Нейгебауеру вычисление соответствовало схеме:
| В одном доме | |||||||
| В двух домах | |||||||
| В четырех домах | |||||||
| Вместе 7 | В семи домах |
Рассмотрим задачи:
а) на геометрическую прогрессию
Задача Леонарда.
«7 старух идут в Рим, каждая из них имеет 7 посохов, на каждом посохе 7 мешков, в каждом мешке 7 хлебов, в каждом хлебе 7 ножичков, у каждого ножичка 7 ножен. Ищется сумма всего вышеперечисленного».
Леонардо дает 2 решения этой задачи:
1) Непосредственное вычисление: 7+49+343+2401+16807+117649=137256.
2) Пусть имеем только одну старуху; она имеет 7 посохов; общее число предметов  . Такое же количество предметов имелось бы, если бы у нас был один посох с семью мешками. Но посохов 7, значит при семи посохах имеем
. Такое же количество предметов имелось бы, если бы у нас был один посох с семью мешками. Но посохов 7, значит при семи посохах имеем  посохов и мешков. К этому числу добавим 1(предположенное число старух)
посохов и мешков. К этому числу добавим 1(предположенное число старух)  .
.
То же число предметов имеем при одном посохе с его мешками и хлебами. Для семи же посохов имеем  посохов, мешков и хлебов. Присчитаем еще старуху:
посохов, мешков и хлебов. Присчитаем еще старуху:  .
.
И так далее:  есть число всех предметов, начиная с одной старуху и кончая всеми ее посохами, мешками, хлебами и ножами
есть число всех предметов, начиная с одной старуху и кончая всеми ее посохами, мешками, хлебами и ножами  есть то же число вместе с ножнами.
есть то же число вместе с ножнами.
Последнее число множается на 7, т.к. в действительности число старух не 1, а 7 отсюда следует,  .
.
б) на арифметическую прогрессию.
«Пусть сказано разделить 10 мер ячменя между 10 человеками; разница между каждым человеком и его соседом составляет 8 мер ячменя (средняя доля есть одна мера).
Решение. Вычти 1 из 10. Остаток есть 9. Составь половину разницы; это есть  . Возьми ее 9 раз; это дает
. Возьми ее 9 раз; это дает  . Приложи это к средней доле; вычитай для каждого лица по
. Приложи это к средней доле; вычитай для каждого лица по  меры, пока не достигнешь конца».
меры, пока не достигнешь конца».
Итак ход решения можно представить так: пусть S – сумма убывающей арифметической прогрессии (S=10), n=10 – число ее членов, d=  - разность,
- разность, 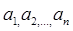 - ее члены, начиная с наибольшего. Итак:
- ее члены, начиная с наибольшего. Итак:
1. Образуется среднее арифметическое 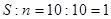 .
.
2. Из числа членов отнимается единица  .
.
3. Составляется полуразность прогрессий  .
.
4. Полуразность умножается на число членов без одного:
 .
.
5. Прибавлением результата к среднему арифметическому находится первый член прогрессии
 .
.
6. Остальные члены находятся последовательным вычитанием разности
 ,
,
 и т.д.
и т.д.
В основу положено правило (формула)  . Решение этой задачи показывает, что здесь не может быть речи об алгебраической трактовке вопроса, имеем дело с обычным арифметическим рассуждением.
. Решение этой задачи показывает, что здесь не может быть речи об алгебраической трактовке вопроса, имеем дело с обычным арифметическим рассуждением.
7. Геометрические знания египтян относятся к измерению площадей и объёмов. Некоторые найденные при этом результаты были замечательными, но в отдельную отрасль математики геометрия ещё не превратилась.
Площади прямоугольников, треугольников и трапеций вычислялись по точным правилам, площадь произвольного четырёхугольника по приближённому правилу, как произведение полусумм пар противоположных сторон a,c и b,d т.е.  .
.
Этой формулой пользовались и при определении площади треугольника при d=0. Все эти задачи возникли из практики землемерия.
Мы то знаем, что это правило приближённое, знали ли об этом землемеры, это вопрос, на который мы не сможем ответить.
Вычисление S круга.
Египтяне пользовались хорошим приближением, полагая площадь S круга равной квадрату со стороной в 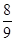 диаметра:
диаметра:  . Метод получения правила неизвестен. Правдоподобна гипотеза А.Е. Райк о последовательности наложения квадратных сеток. Предполагается, что площадь круга диаметра d сравнивается с площадью описанного квадрата, из которого удалялись малые квадратики со сторонами
. Метод получения правила неизвестен. Правдоподобна гипотеза А.Е. Райк о последовательности наложения квадратных сеток. Предполагается, что площадь круга диаметра d сравнивается с площадью описанного квадрата, из которого удалялись малые квадратики со сторонами  .
.
Первое приближение:
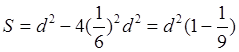 .
.
Второе приближение:

 .
.
Эта формула поражает нас большой степенью точности: ей соответствует значение 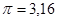 . Большой интерес представляет вопрос о том, как был получен этот результат.
. Большой интерес представляет вопрос о том, как был получен этот результат.
Десятая задача Московского папируса представляет собой древнейший в истории пример вычисления площади кривой поверхности. О какой именно поверхности идёт речь, до сих пор точно не установлено. Согласно утверждению академика В.В. Струве, расшифровавшему и издавшему в 1930 году Московский папирус, речь идёт о «Корзине», обозначаемой символом
 и являющейся полусферой.
и являющейся полусферой.
 Другие исследователи, например Т.Э.Пит считает, что речь идёт о полуцилиндре.
Другие исследователи, например Т.Э.Пит считает, что речь идёт о полуцилиндре.
 Для О. Нейгебауера эта «корзинка» не что иное, как один из куполообразных амбаров (для хранения зерна).
Для О. Нейгебауера эта «корзинка» не что иное, как один из куполообразных амбаров (для хранения зерна).
 Соответствующие вычисления, изложенные в папирусе, приближенные к дробям.
Соответствующие вычисления, изложенные в папирусе, приближенные к дробям.
8.В древнем Египте математика представляла собой совокупность знаний, ещё не расчленившуюся на арифметику, алгебру, геометрию и выступающую прежде всего как собрание правил для численного решения простейших арифметических, алгебраических и геометрических задач. Проблемы, стоявшие перед египетскими чиновниками, были главным образом практические. Многие решения находили путём проб, ощупью и не удивительно, что они оказывались иногда громоздкими и требовали преодоления больших трудностей. Но наряду с этим обобщались задачи и они начинали принимать более абстрактных характер. При исследовании отдельных проблем вырабатываются приёмы геометрических и арифметико-алгебраических преобразований, которые предвещали дальнейший рост этих составных частей математической дедукции.
Математика древнего Египта оказала несомненное влияние на последующие судьбы науки.
Основная литература:
1. Математическая энциклопедия. Книги 1-5. - М.: Советская энциклопедия, 1977-1985.
2. Рыбников К.А. История математики. Уч.пособие для судентов математических специальностей университетов и пед.институтов. 2-е изд. -М.: Изд-во МГУ, 1974.
3. Стройк Д.Я. Краткий очерк истории математики. – Москва: Наука, 1969.
4. Юшкевич А.П. История математики в средние века. - М.: Наука, 1961.
5. История математики с древнейших времен до начала ХІХ столетия. В 3-х томах. Под.ред А.П.Юшкевича.-М.: Наука, 1970-1972.
6. Нейгебауэр О. Точные науки в древности – М: Наука, 1968.
Дополнительная литература:
1. Хрестоматия по истории математики. Под.ред. А.П.Юшкевича. – М.: Просвещение, 1976, 1977.
2. Глейзер Г.И. История математики в средней школе в 3-х кн..-М.: Просвещение, 1981-1983.
3. Депман И.Я., Виленкин Н.Я. «За страницами учебника». - М.: Просвещение, 2002.
4. Стройк Д.Я. Краткий очерк истории математики. – Москва: Наука, 1969.
|
|
|


