 |
Cвязанные динамические структуры данных
|
|
|
|
Несвязанные динамические структуры данных.
Одномерные массивы
Если до начала работы неизвестно, сколько в массиве элементов, то следует использовать динамические массивы. Память под них выделяется с помощью функции new во время выполнения программы.
int n = 10;
int *b = new int; // выделение памяти для переменной целого типа
int *a = new int [n]; // выделение памяти для массива переменных целого типа
Переменная а – указатель на целую величину, которому присваивается адрес непрерывной области динамической памяти, выделенной функцией new. Выделяется столько памяти, сколько необходимо для хранения n величин типа int.
Обнуление памяти при ее выделении не происходит.
Инициализировать динамический массив нельзя.
Обращение к элементу динамического массива происходит также, как и к элементу обычного – например a[2] или *(a + 2).
Если динамический массив в какой-то момент работы программы перестает быть нужным, то необходимо освободить память с помощью функции delete, например
delete [] a;
delete b;
Двумерные массивы.
Существует 2 способа организации работы с двумерным массивом.
1 способ.
Двумерный массив можно представить в виде одномерного, а «двумерность» учитывать при обращении к элементам массива. Обращение к элементу одномерного массива Аr[i*ncol + j] есть фактически обращение к элементу двумерного массива A с индексами i, j.
 |
A[0][0] A[0][1] A[0][2] A[1][0] A[1][1] A[1][2] A[2][0] A[2][1] A[2][2]
Ar[0] Ar[1] Ar[2] Ar[3] Ar[4] Ar[5] Ar[6] Ar[7] Ar[8]
Описание
int *Array;
int nrow, ncol; // размерности матрицы
Выделение памяти:
Array = new int [nrow * ncol];
Освобождение памяти:
delete [] Аrray;
Обращение к элементу [i][j]: Array[f(i, j, ncol)]
где f(i, j, ncol) = i * ncol + j - определение номера элемента [i][j] матрицы в одномерном массиве
|
|
|
2 способ.
Двумерный массив представляется как указатель на массив указателей на строки матрицы.
int **A int *A[n] int A[n][m]

Описание
int **Array;
int nrow, ncol; // размерности матрицы
Выделение памяти:
//выделяется память под массив указателей на строки массива
Array = new int* [nrow];
// цикл для выделения памяти под строки массива
for (int i = 0; i < nrow; i++)
Array[i] = new int [ncol];
Освобождение памяти:
for (int i = 0; i < nrow; i++)
delete Array[i];
delete [] Array;
Обращение к элементу [i][j]:
Array[i][j]
Cвязанные динамические структуры данных
Связанные динамические структуры по определению характеризуются отсутствием физической смежности элементов структуры в памяти, непостоянством и непредсказуемостью размера (числа элементов) структуры в процессе ее обработки.
Поскольку элементы динамической структуры располагаются по непредсказуемым адресам памяти, адрес элемента такой структуры не может быть вычислен из адреса начального или предыдущего элемента. Для установления связи между элементами динамической структуры используются указатели, через которые устанавливаются явные связи между элементами.
Такое представление данных в памяти называется связным.
Элемент динамической структуры состоит из двух полей:
- информационного поля или поля данных, в котором содержатся те данные, ради которых и создается структура; в общем случае информационное поле само является интегрированной структурой - вектором, массивом, другой динамической структурой и т.п.;
- поле связок, в котором содержатся один или несколько указателей, связывающий данный элемент с другими элементами структуры.
Когда связное представление данных используется для решения прикладной задачи, для конечного пользователя "видимым" делается только содержимое информационного поля, а поле связок используется только программистом-разработчиком.
|
|
|
Достоинства связного представления данных - в возможности обеспечения значительной изменчивости структур:
- размер структуры ограничивается только доступным объемом машинной памяти;
- при изменении логической последовательности элементов структуры требуется не перемещение данных в памяти, а только коррекция указателей;
- большая гибкость структуры.
Вместе с тем связное представление не лишено и недостатков, основные из которых:
- на поля связок расходуется дополнительная память;
- доступ к элементам связной структуры может быть менее эффективным по времени.
Последний недостаток является наиболее серьезным и именно им ограничивается применимость связного представления данных. Если в смежном представлении данных для вычисления адреса любого элемента нам во всех случаях достаточно было номера элемента и информации, содержащейся в дескрипторе структуры, то для связного представления адрес элемента не может быть вычислен из исходных данных. Дескриптор связной структуры содержит один или несколько указателей, позволяющих войти в структуру, далее поиск требуемого элемента выполняется следованием по цепочке указателей от элемента к элементу. Поэтому связное представление практически никогда не применяется в задачах, где логическая структура данных имеет вид вектора или массива - с доступом по номеру элемента, но часто применяется в задачах, где логическая структура требует другой исходной информации доступа.
Связные динамические структуры можно разделить на списки, графы, деревья.
Список - последовательность однородных элементов (называемых узлами), каждый из которых содержит ссылку на следующий (и/или предыдущий) элемент.
Списки делятся на линейные и кольцевые.
Списки делятся на односвязные и двусвязные.
Размер списка - количество элементов списка.
Список, в котором нет элементов, называется пустым списком.
Узлом списка называют элемент списка. Узел в связном списке состоит из двух частей. Первая часть содержит непосредственно данные, вторая часть содержит один или несколько адресов элементов, с которым связан данный узел.
|
|
|
Список, в узлах которого, задается адрес только одного (предыдущего или последующего) элемента, называются однонаправленным (односвязным).
Список, в узлах которого, задаются адреса и предыдущего и последующего элементов, называются двунаправленным (двусвязным).
Указатель на первый элемент списка – это адрес списка. Значение «NULL» (“0”) этого указателя означает, что список пуст.
Линейным списком называется последовательность однородных элементов (называемых узлами), каждый из которых (кроме последнего) содержит ссылку на следующий (и/или предыдущий) элемент.
Линейный список может быть односвязным и двусвязным.
Линейные списки делятся на стеки, очереди, линейные списки.
Линейные списки – данные динамической структуры, которые представляют собой совокупность линейно связанных однородных элементов, для которых разрешается добавлять элементы между любыми двумя другими и удалять любой элемент.

Очередь – частный случай линейного списка – разрешено только 2 действия – добавление элементов в конец (хвост) и удаление из начала (головы) списка.

Стек – частный случай линейного списка – разрешено только 2 действия – добавление и удаление элементов с одного конца (головы) стека.

Кольцевой список – это линейный список, последний элемент которого содержит ссылку на первый элемент списка.
Кольцевой список также как линейный список может быть односвязным и двусвязным.

Деревья – иерархические динамические структуры, состоящие из узлов, каждый из которых содержит, кроме данных, ссылки на различные деревья. На каждый узел имеется ровно одна ссылка. Начальный узел называется корнем дерева.
Бинарное дерево – это динамическая структура данных, состоящая из узлов, каждый из которых содержит, кроме данных, не более двух ссылок на различные бинарные деревья.

Граф – самая общая нелинейная динамическая структура данных. В графе каждый узел содержит несколько указателей на несколько узлов.
|
|
|

Стек
Стек – частный случай односвязного линейного списка – разрешено только 2 действия – добавление и удаление элементов с одного конца (головы) стека. Другие операции со стеком не определены.
Стек реализует принцип обслуживания LIFO (Last In – First Out, последний пришел – первый ушел).

Базовые операции над стеком:
· добавление в стек нового элемента, новый элемент помещается в вершину стека;
· чтение данных из вершины стека («выталкивание» верхнего элемента);
· вывод всех элементов стека;
Реализация стека в виде массива
Если заранее известно максимальное количество элементов (l), одновременно хранящихся в стеке, то целесообразно моделировать стек на массиве A постоянной длины. Пусть переменная top содержит индекс последнего включенного в стек элемента (первоначально top =-1), тогда процедуры включения и исключения элемента из стека реализуются следующим образом:
Включение элемента x в стек А Исключение элемента из стека А
if (top < l - 1) if (top >= 0)
{ {
top++; x = A[top];
A[top] = x; top--;
} }
Реализация стека в виде связных компонент
Элемент стека состоит из полей разной природы, поэтому описывается через структуру, где основное поле – это поле для указания адреса следующего элемента в стеке.
Описание элемента стека:
struct Node
{
int d; // поля произвольных типов
Node *link; // указатель на следующий элемент стека
};
Алгоритм вычисления выражений через обратную польскую запись
Обычные алгебраические (логические, математические) выражения можно записывать в виде обратной польской нотации – записи без скобок.
Нотация – «польская» в честь польского математика Яна Лукашевича, который ее предложил. Нотация – «обратная» из-за того, что порядок операндов и операций обратный относительно исходного.
Пример:
Выражение Обратная польская нотация
А + (В - С) * D – F / (G + H) = à A B C – D * + F G H + / - =
Если A = 6 B = 4 C = 1 D = 2 F = 3 G = 7 H = 5.
Тогда обратная польская нотация: 6 4 1 – 2 * + 3 7 5 + / - =
Алгоритм вычисления выражения.
Вычислить обратное польское выражение проще, чем обычное алгебраическое.
Просматриваем все элементы слева направо. Как только встречается операция, выполняем ее по отношению к двум предыдущим элементам, заменяя два элемента одним.
6 4 1 – 2 * + 3 7 5 + / - = выполняем 4-1=3 à
6 3 2 * + 3 7 5 + / - = выполняем 3*2=6 à
6 6 + 3 7 5 + / - = выполняем 6+6=12 à
12 3 7 5 + / - = выполняем 7+5=12 à
12 3 12 / - = выполняем 3/12=0.25 à
12 0.25 - = выполняем 12-0.25=11.75 à
11.75 = результат
Алгоритм преобразования выражения в обратную польскую нотацию.
|
|
|
Необходимо использовать два стека (списка) Х и Y.
Необходимо определить приоритеты операций. Например, так:
операции приоритет
* / 3
+ - 2
(1
= 0
1. Просматриваем выражение слева направо. Операнды помещаем в стек X, левые скобки и операции в стек Y.
2. Встретив правую скобку, отыскиваем в стеке соответствующую ей левую. При этом все, что сверху – выталкивается из стека Y и заносится в стек X.
3. Если приоритет очередной операции меньше приоритета операции вершины стека, то операции из вершины стека Y выталкиваются в стек Х, пока не найдем операцию с приоритетом ниже, либо пока стек не окажется пустым.
4. Результат оказывается с стеке X.
Пример преобразования выражения в обратную польскую запись
А + (В - С) * D – F / (G + H) =
стек X стек Y
1. A
A
2.+
A +
3. (
A (à +
4.B
B à A (à +
5. -
B à A - à (à +
6. C)
C à B à A - à (à +
7.)
- à C à B à A +
8. *
- à C à B à A * à +
9. D
D à - à C à B à A * à +
10. –
+ à * à D à - à C à B à A -
11. F
F à + à * à D à - à C à B à A -
12. /
F à + à * à D à - à C à B à A / à -
13. (
F à + à * à D à - à C à B à A (à /à -
14. G
G à F à + à * à D à - à C à B à A (à / à -
15. +
G à F à + à * à D à - à C à B à A + à (à / à -
16. H
H à G à F à + à * à D à - à C à B à A +à (à /à -
17.)
+ à H à G à F à +à *à D à - à C à B à A / à -
18. =
- à / à + à H à G à F à + à *à Dà - à Cà Bà A
результат в обратном порядке
A B C – D * + F G H + / - =
Очередь
Очередь – частный случай односвязного линейного списка – разрешено только 2 действия – добавление элементов в конец (хвост) и удаление из начала (головы) списка. Другие операции со стеком не определены.
Очередь реализует принцип обслуживания FIFO (First In – First Out, первый пришел – первый ушел).

Базовые операции над очередью:
· добавление в очередь нового элемента, новый элемент помещается в конец очереди;
· чтение данных из начала очереди («выталкивание» первого элемента);
· вывод всех элементов очереди;
Реализация очереди в виде массива
Если заранее известно максимальное количество элементов (l), одновременно хранящихся в очереди, то целесообразно моделировать очередь на массиве A постоянной длины. С очередью свяжем две переменные top и end, определяющие индексы первого и последнего элементов очереди и переменную булевского типа empty, которая равна true в случае, когда очередь пуста. Тогда процедуры включения и исключения элемента из очереди реализуются следующим образом:
Включение элемента x в очередь А Исключение элемента из очереди А
if (empty) if (!empty)
{ top = 0; {
A[top] = x; x = A[top];
empty = false;
end = top; if (top == end)
} empty = true;
else top++;
{ end++; }
if (end < l)
A[end] = x;
}
Реализация очереди в виде связных компонент
Описание элемента очереди:
struct Node
{
int d; // поля произвольных типов
Node *link; // указатель на следующий элемент очереди
};
При работе с очередью можно использовать один указатель на начало очереди или два указателя: один на начало очереди, другой – на её конец. Использование двух указателей упрощает алгоритм добавления нового элемента.
Список
Линейные списки – данные динамической структуры, которые представляют собой совокупность линейно связанных однородных элементов, для которых разрешается добавлять элементы между любыми двумя другими и удалять любой элемент.

Реализация списка в виде двух массивов
Список можно реализовать в виде двух массивов А и В.
Пусть i – индекс элемента в списке, тогда A [ i ] – сам элемент, B [ i ] – индекс следующего элемента в списке A. Если k – индекс последнего элемента в списке, то B [ k ] = 0. Кроме того, существуют две переменные: nz – индекс начала занятых компонент и ns – индекс начала свободных компонент.
Пример.
Список 2, 12, 17 будет реализован следующим образом:
 А
А
 В
В
nz = 0 ns = 3
Реализация списка в виде связанных компонент
Описание элемента линейного односвязного списка аналогично описанию очереди и стека:
struct Node
{
int d; // поля произвольных типов
Node *link; // указатель на следующий элемент списка
};
Описание элемента линейного двусвязного списка:
struct Node
{
int d; // поля произвольных типов
Node *next; // указатель на следующий элемент списка
Node *pred; // указатель на предыдущий элемент списка
};
Базовые операции над списком:
· начальное формирование списка (создание первого элемента списка);
· добавление элемента в список;
· нахождение заданного элемента;
· вставка элемента в список;
· удаление элемента из списка;
· упорядочивание элементов списка;
· объединение двух списков;
· разделение списка на 2 списка;
· копирование списка;
· определение количества узлов списка;
· чтение и вывод всех элементов списка.
Удаление элемента в списке
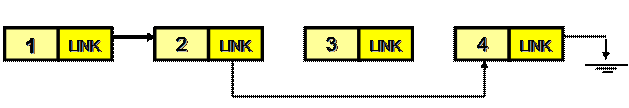
Пусть
· адрес элемента, который нужно удалить содержится в переменной pv.
· адрес предыдущего элемента – в переменной ppv.
Чтобы удалить элемент с ключом 3 (адрес pv), необходимо изменить связи так, чтобы элемент с ключом равным 2 (ppv), указывал (ppv -> link) на элемент с ключом равным 4 (pv -> link).
Вставка элемента в список


 |

Пусть
· адрес элемента, который нужно вставить nv.
· адрес элемента, перед которым нужно вставить элемент содержится в переменной pv.
· арес предыдущего элемента – в переменной ppv.
Тогда, чтобы вставить элемент с ключом 2.5 (nv), необходимо изменить связи так, чтобы:
· элемент с ключом 2 (ppv), указывал (ppv -> link) на элемент с ключом 2.5 (nv),
· элемент с ключом 2.5 (nv) указывал (nv -> link) на элемент с ключом 3 (pv).
Удаление элемента в двусвязном списке





 | |||
 |
Пусть
· адрес элемента, который нужно удалить содержится в переменной pv.
· адрес предыдущего элемента – в переменной ppv.
Чтобы удалить элемент с ключом 2 (адрес pv), необходимо изменить связи так, чтобы
· элемент с ключом 1 (ppv), указывал (ppv -> next) на элемент с ключом 3 (pv -> next).
· элемент с ключом 3 (pv -> next), указывал (pv -> next -> pred) на элемент с ключом 1 (ppv).
Вставка элемента в двусвязный список
 | |||
 | |||

 |  | ||||
 | |||||

 |
Пусть
· адрес элемента, который нужно вставить nv.
· адрес элемента, перед которым нужно вставить элемент содержится в переменной pv.
· адрес предыдущего элемента – в переменной ppv.
Чтобы вставить элемент с ключом равным 1.5 (nv), необходимо изменить связи так, чтобы:
· элемент с ключом 1 (ppv), указывал (ppv->next) на элемент с ключом 1.5 (nv),
· элемент с ключом 1.5 (nv), указывал (nv->next) на элемент с ключом 2 (pv),
· элемент с ключом 1.5 (nv) указывал (nv->pred) на элемент с ключом 1 (ppv).
· элемент с ключом 2 (pv) указывал (pv->pred) на элемент с ключом 1.5 (nv).
Бинарное дерево
Дерево – нелинейная динамическая структура данных. В дереве каждый узел содержит несколько указателей на несколько узлов.
Бинарное дерево – это динамическая структура данных, состоящая из узлов, каждый из которых содержит, кроме данных, не более двух ссылок на различные бинарные деревья. На каждый узел имеется ровно одна ссылка.
Начальный узел называется корнем дерева. У корневого узла нет входящих в него ветвей, есть только исходящие. Узлы корневого дерева, не имеющие ссылок на другие узлы, называются листьями.
Исходящие узлы называются предками, входящие – потомками.
Высота дерева определяется количеством уровней, на которых располагаются его узлы.
Высота двоичного дерева не более log 2 n.

Одним из специальных случаев бинарных деревьев являются полные бинарные деревья. Полным бинарным деревом называют упорядоченное корневое дерево, в котором:
· каждая вершина имеет не более двух потомков;
· заполнение дерева осуществляется от корня к листьям по уровням;
· заполнение уровней производится слева направо.
Если дерево организовано таким образом, что для каждого узла все ключи его левого поддерева меньше ключа этого узла, а все ключи его правого поддерева – больше, оно называется деревом поиска. Одинаковые ключи не допускаются.
Дерево называется идеально сбалансированным, если оно является бинарным деревом поиска и число вершин в его левых и правых поддеревьях отличается не более чем на 1.
Дерево называется сбалансированным, если оно является бинарным деревом поиска и высоты двух поддеревьев каждой из его вершин отличаются не более чем на 1. Такие деревья часто называют АВЛ-деревьями (по именам открывателей Г.М. Адельсон-Вельский и Е.М. Ландис).
Все идеально сбалансированные деревья являются также АВЛ-деревьями.
Реализация бинарного дерева в виде двух массивов
Бинарное дерево можно реализовать в виде двух массивов Left и Right. Если узел j является левым непосредственным потомком узла i, то Left [ i ] = j; если узел j является правым непосредственным потомком узла i, то Right [ i ] = j; если у узла i нет левого непосредственным потомка, то Left [ i ] = 0; если у узла i нет правого непосредственным потомка, то Right [ i ] = 0.
Полные бинарные деревья обычно представляют в виде одномерного массива R. R [0] – корень дерева, а для произвольного узла I его левый непосредственным потомок располагается в элементе R [2 i ], а правый – R [2 i +1]. Непосредственный предок узла, находящегося в позиции j, расположен в позиции [ j/2 ].
Реализация дерева в виде связанных компонент
Описание элемента бинарного дерева:
struct Node
{
int d; // поля произвольных типов
Node *left; // указатель на левое поддерево
Node *right; // указатель на правое поддерево
};
Базовые операции над бинарным деревом:
§ построить дерево;
§ добавить новый элемент к дереву;
§ выполнить поиск элемента с заданным значением ключа;
§ выполнить обход элементов дерева для выполнения над ними некоторой операции;
§ удаление узла с заданным значением ключа;
§ уничтожение дерева и освобождение памяти.
Дерево является рекурсивной структурой данных, поскольку каждое поддерево также является деревом. Действия с такими структурами лучше всего описываются с помощью рекурсивных алгоритмов.
Обход дерева можно осуществить тремя способами:
1. Обход слева направо: L, K, R (сначала посещаем левое поддерево, затем корень и, наконец, правое поддерево) – инфиксный порядок обхода. Для дерева поиска такой порядок обхода дерева позволяет получить отсортированную последовательность.
void inorder (Node *top)
{
if (top)
{
inorder(top -> left);
P(top); // операция над вершиной дерева
inorder(top -> right);
}
}
Или справа налево: R, K, L (сначала посещаем правое поддерево, затем корень и, наконец, левое поддерево).
void inorder (Node *top)
{
if (top)
{
inorder(top -> right);
P(top); // операция над вершиной дерева
inorder(top -> left);
}
}
2. Обход сверху вниз K, L, R (посещаем корень до поддеревьев) – префиксный порядок обхода.
void preorder (Node *top)
{
if (top)
{
P(top); // операция над вершиной дерева
preorder(top -> left);
preorder(top -> right);
}
}
3. Обход снизу вверх L, R, K (посещаем корень после поддеревьев) – постфиксный порядок обхода.
void postorder (Node *top)
{
if (top)
{
postorder(top -> left);
postorder(top -> right);
P(top); // операция над вершиной дерева
}
}
Граф
Граф — это совокупность непустого множества объектов и множества пар этих объектов. Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра.
Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах. Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Учебника можно смоделировать при помощи ориентированного графа (орграф), в котором вершины — это статьи, а дуги (ориентированные рёбра) — гиперссылки.
Граф – G = (V, E) состоит из V - конечного непустого множества элементов (называемых узлами или вершинами), и E - множества неупорядоченных пар (u, v) вершин из V, называемых ребрами.
Ребро s = (u, v) соединяет вершины u, v. Ребро s и вершина u (а также s и v) называются инцидентными, а вершины u и v – смежными.
Графы бывают: ориентированные и неориентированные, связные и несвязные, полные, двудольные, мультиграфы и т.д..
Пустой граф – граф с пустым множеством вершин.
Ориентированный граф, или орграф, G = (V, E) отличается от графа тем, что Е – множество упорядоченных пар (u, v) вершин u, v Î V, называемых дугами. Дуга (u, v) ведет от вершины u к вершине v.
Если некоторая пара вершин соединена несколькими ребрами, то граф называется мультиграфом.
На практике граф изображают следующим образом (вершины – точками, ребра – линиями (или для ориентированного графа направленными линиями):
 |
Существует множество алгоритмов на графах, в основе которых лежит такой перебор вершин графа, при котором каждая вершина просматривается ровно один раз:
· поиск в глубину;
· поиск в ширину;
· топологическая сортировка.
· нахождение кратчайшего пути;
· максимальный поток;
· минимальное остовное дерево;
Способы представления графа в памяти.
1. С использованием массивов - матрица смежности, матрица инцендентности.
2. С использованием последовательно связанных элементов – список ребер, список смежности.
Определения.
Количество вершин графа называется его порядком.
Количество ребер графа называется его размером.
Если между вершинами существует ребро, то вершины называются смежными.
Число ребер, инцедентных некоторой вершине, называется степенью данной вершины.
Путь, соединяющий вершины u, v, – это последовательность вершин v 0, v 1, …, vn такая, что v 0 = u, vn = v и для любого i вершины vi и v i+1 соединены ребром.
Длина пути равна количеству ребер.
Путь замкнут, если v 0 = vn .
Путь называется простым, если все его вершины различны.
Замкнутый путь, в котором все ребра различны, называется циклом.
Расстояние между двумя вершинами – длина кратчайшего пути, соединяющего эти вершины.
Граф называется связным, если для любой пары вершин существует соединяющий их путь.
При этом вершину v называют преемником вершины u, а u – предшественником вершины v.
Деревом называется связный граф без циклов.
Корневое дерево – ориентированный граф, который удовлетворяет следующим условиям:
· имеется точно один узел (корневой), в который не входит ни одна дуга;
· в каждый узел, кроме корня входит ровно одна дуга;
· из корня имеется путь в каждый узел.
Способы представления графа в памяти
1. Матрица смежности
Классическим способом задания графа является матрица смежности А рамера n x n (n – количество вершин графа), где А [ i ][ j ] =1, если существует ребро(дуга), идущее из вершины i в j, и А [ i ][ j ] =0 в противном случае.
Матрица смежности неориентированного графа является симметричной матрицей, на главной диагонали которой стоят нули.
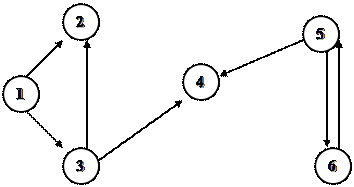 |
Для орграфа, представленного на рисунке, матрица смежности:
1 2 3 4 5 6
 |
1 0 1 1 0 0 0
2 0 0 0 0 0 0
3 0 1 0 1 0 0
4 0 0 0 0 0 0
5 0 0 0 1 0 1
6 0 0 0 0 1 0
Недостатками такого представления являются:
· объем памяти вне зависимости от количества ребер (дуг) составляет n 2;
· необходимо заранее знать количество вершин графа.
2. Матрица инцедентности
Другим традиционным способом представления графа служит матрица инцедентности. Эта матрица А рамера n x m, где n – количество вершин графа, а m – количество ребер графа. Для орграфа столбец, соответствующий дуге (i, j) содержит 1 в строке, соответствующей вершине i, содержит -1 в строке, соответствующей вершине j, и нули во всех остальных строках.
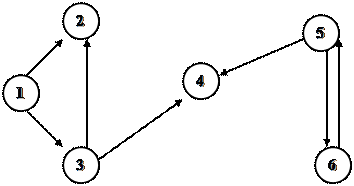 |
Для орграфа, представленного на рисунке, матрица инциндентности:
 |
(1,2) (1,3) (3,2) (3,4) (5,4) (5,6) (6,5)
 |
1 1 1 0 0 0 0 0
2 -1 0 -1 0 0 0 0
3 0 -1 1 1 0 0 0
4 0 0 0 -1 -1 0 0
5 0 0 0 0 1 1 -1
6 0 0 0 0 0 -1 1
Недостатками такого представления являются:
· объем памяти составляет nm ячеек, которые в большинстве заполнены нулями;
· чтобы проверить существование дуги между вершинами, необходим перебор столбцов матрицы;
· необходимо заранее знать количество вершин графа.
3. Список пар (список ребер)
Более экономным в отношении памяти, особенно если m << n 2, является метод представления графа с помощью списка пар, соответствующих ребрам: пара i, j соответствует ребру(i, j)
 |
Для орграфа, представленного на рисунке:
Объем памяти в этом случае составляет О(m), но необходимо большое количество шагов для получения множества вершин, к которым ведут ребра из заданной вершины.
4. Список смежности
Во многих ситуациях наиболее приемлемым способом задания графа является структура данных, которую называют списками смежности.
struct SP
{
int key; // номер смежной вершины
SP *next; // указатель на следующую смежную вершину
};
SP *GRAF[n];
В этом случае GRAF – массив, i –й элемент которого является указателем на начало линейного списка вершин, смежных с i –ой вершиной; если из вершины i нет выходящих дуг, то GRAF[i] = NULL. Таким образом, граф представлен в виде n списков смежности, по одному для каждой вершины.
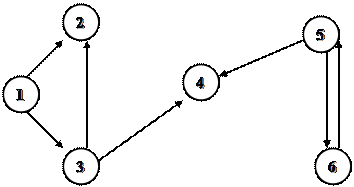
Для орграфа, представленного на рисунке:
GRAF
 |
Объем памяти в этом случае О(n + m), но необходимо заранее знать количество вершин графа.
5. Список смежности
Во многих ситуациях вершины в граф добавляются в ходе выполнения программы, т.е. количество вершин графа может быть неизвестно заранее. Тогда наиболее приемлемым способом задания графа является структура данных, которую называют списками смежности, но граф представляется не массивом таких списков, а тоже линейным списком, в котором обязательны поля: номер вершины графа, указатель на список смежных с данной вершин, указатель на следующую вершину графа.
struct SP
{
int key; // номер смежной вершины
SP *next; // указатель на следующую смежную вершину
};
struct GRAF
{
int NV; // номер вершины
SP *spis_sv; //указатель на линейный список смежных вершин
GRAF *next; //указатель на следующую вершину графа
};
Для орграфа, представленного на рисунке:
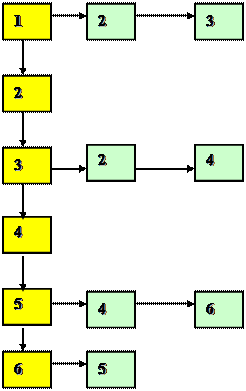 |
ПРИМЕРЫ
Пример 1. Динамический одномерный массив
Следующая программа определяет сумму элементов массива любой размерности.
#include <iomanip> // for cetw
#include <iostream> // for cin cout
using namespace std;
double sum (int *, int);
void zapolnenie (int *, int);
void vyvod (int *, int);
int main()
{
int n;
double Result;
cin >> n; // n - размерность массива
int *Array = new int[n]; // выделение памяти для массива
// проверка на корректность выделения памяти
if (!Array)
return 1;
zapolnenie(Array,n); // заполнение массива
vyvod(Array,n); // вывод элементов массива на экран
// передача динамического массива в функцию
Result = sum(Array, n);
cout << "Result="<<Result<<endl;
delete []Array; // освобождение памяти
return 0;
}
//---------------- функция заполнения массива размерности n
void zapolnenie(int *array, int n)
{
for (int i = 0; i < n; i++)
array[i] = i;
}
//-------------------------- функция
|
|
|


