 |
Тема 18. Общие сведения о строительных чертежах
|
|
|
|
Стандарты СПДС - системы проектной документации для строительства. Содержание и виды строительных чертежей. Масштабы строительных чертежей.
Литература: [3, с. 96-99].
Вопросы для самопроверки
1. Как обозначаются стандарты СПДС?
2. Перечислите виды строительных чертежей.
3. Назовите масштабы строительных чертежей.
Тема 19. Чертежи узлов строительных конструкций
Состав рабочих чертежей. Масштабы изображения. Графическое оформление. Узел металлической фермы.
Литература: [3, с. 134-161].
Вопросы для самопроверки
1. Какие особенности необходимо учесть при графическом оформлении чертежей металлических строительных изделий?
2. Как показывают на металлических строительных изделиях профиль материалов?
3. Как соединяют детали металлических изделий между собой?
4. Как изображают сварные швы на изделии?
Тема 20. Архитектурно-строительные чертежи
Стадии проектирования. Архитектурно-строительные чертежи:
планы, фасады, разрезы.
Литература: [2, с. 293-308]; [3, с. 109-131].
Вопросы для самопроверки
1. Что называют координационными осями здания и как они маркируются на плане и разрезе?
2. В чем особенности обводки линий на планах, разрезах и фасадах зданий?
3. Что называют планом здания?
4. По каким частям здания следует проводить секущую плоскость при выполнении чертежа разреза здания?
5. Какие размеры и отметки наносят на чертежах разрезов, фасадов зданий?
Контрольные работы
Контрольные работы выполняются по мере освоения курса дисциплины. Основной формой работы студента является самостоятельное изучение материала по учебнику и учебным пособиям, а также по соответствующим стандартам системы ЕСКД и СПДС. При выполнении контрольной работы студенты закрепляют усвоенный материал, приобретают навыки по составлению, оформлению конструкторской документации.
|
|
|
Программный материал рекомендуется изучать в следующей последовательности:
1. Ознакомиться с общими методическими указаниями данного пособия и содержанием программы.
2. Изучить материал по темам задания. Ответить на вопросы для самоконтроля.
3. Приступить к выполнению заданий контрольной работы.
Задания на контрольные работы
Задания на контрольную работу №1
Лист 1
Выполняется титульный лист и содержание контрольных работ по рис. 47 (см. п. 6).
Лист 2
Выполнить три задачи на точку, прямую и плоскость в ортогональных проекциях. Пример выполнения листа приведен на рисунке 1. Задачи 1 и 2 совместить на одном чертеже в левой части листа, а задачу 3 расположить в правой части листа. Точку Е построить только для задачи 3. Для левой и правой частей листа координатные оси показывать раздельно.
Основная надпись выполняется по форме 4 (рис.52).
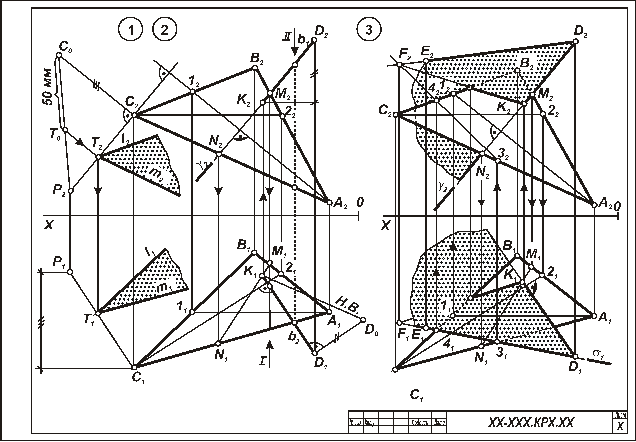
Рисунок 1 - Образец выполнения листа 2
Задача 1. Дано: плоскость треугольника α (А, В, С) и точка D. Требуется определить расстояние от точки D до плоскости, заданной треугольником α (А, В, С). Определить видимость перпендикуляра, проходящего через точку D по отношению к плоскости треугольника α (А, В, С). Данные для выполнения задачи взять из таблицы 1 в соответствии с вариантом.
Указания к выполнению задачи 1 (рис. 1). Задачу выполняют в такой последовательности: 1) из точки D опустить перпендикуляр, используя горизонталь h и фронталь f плоскости. При этом горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали h1, а фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали f2; 2) определить точку пересечения перпендикуляра с плоскостью α (A, В, С), для чего перпендикуляр (прямую) заключают во вспомогательную, обычно проецирующую, плоскость (γ), находят линию пересечения плоскости α (А, В, С) и вспомогательной γ и отмечают точку К, в которой эта линия пересекается с перпендикуляром; 3) определяют натуральную величину (Н.В.) расстояния от точки D до плоскости α (А, В, С), применяя способ прямоугольного треугольника; 4) видимость проекции перпендикуляра определяют методом конкурирующих точек.
|
|
|
Таблица 1
| Номер вар-та | Значения координат, мм | ||||||||||||||
| ХА | YА | ZA | XB | YB | ZB | XC | YC | ZC | XD | YD | ZD | XE | YE | ZE | |
Задача 2 (рис. 1). Дано: плоскость треугольника α (А, В, С). Требуется: построить плоскость, параллельную заданной и отстоящую от нее на 45 – 50 мм. Данные для выполнения задачи взять из таблицы 1.
Указания к выполнению задачи 2. Задачу выполняют в такой последовательности: 1) в заданной плоскости α (А, В, С) выбирают произвольную точку (в том числе вершину, на рисунке 1 взята точка С) и из нее восстанавливают перпендикуляр к плоскости α (А, В, С) (аналогично первому действию в задаче 1); 2) определяют методом прямоугольного треугольника натуральную величину произвольного отрезка перпендикуляра, который ограничивают произвольной точкой Р; 3) на натуральной величине произвольного отрезка перпендикуляра находят точку Т, расположенную на заданном расстоянии 45 мм от плоскости, и строят проекции этой точки на проекциях перпендикуляра; 4) через точку Т строят искомую плоскость, соблюдая условие параллельности плоскостей: если плоскости параллельны, то две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости. На эпюре одноименные проекции пересекающихся прямых параллельны.
|
|
|
Задача 3 (рисунок 1). Дано: плоскость треугольника α(А, В, С) и прямая а (D, Е). Требуется: через прямую а(D, Е) провести плоскость, перпендикулярную плоскости треугольника α (А, В, С), построить линию пересечения этих двух плоскостей, определить видимость. Данные для выполнения задачи взять из таблицы 1.
Указания к выполнению задачи 3. Решение задачи включает следующие действия: 1) строят плоскость, перпендикулярную плоскости
α (А, В, С). Плоскость, перпендикулярная другой плоскости, должна проходить через перпендикуляр к этой плоскости. Искомая плоскость, перпендикулярная плоскости α (А, В, С), должна содержать в себе заданную прямую а (D, Е) и перпендикуляр, опущенный из любой точки этой прямой на заданную плоскость α (А, В, С); (например, из точки D); 2) строят линию пересечения двух плоскостей: заданной плоскостью треугольника α (А, В, С) и построенной, перпендикулярной ей. Задачу на определение линии пересечения двух плоскостей можно решить двумя способами: первый – построить точки пересечения двух прямых одной плоскости с другой плоскостью, т. е. использовать два раза схему нахождения точки пересечения прямой с плоскостью; второй – ввести две вспомогательные секущие плоскости частного положения, которые одновременно пересекали бы плоскость α (А, В, С) и плоскость, перпендикулярную ей, построить их линии пересечения с заданными плоскостями. Две собственные точки пересечения этих линий определяют линию пересечения данных плоскостей. На примере выполнения листа 2 (рисунок 1) в задаче 3 применен первый способ. Точки пересечения прямой а (D, Е) и перпендикуляра b (D, К) определяют линию пересечения плоскостей α (А, В, С) и искомой перпендикулярной к ней;
|
|
|
3) определяют видимость пересекающихся заданных плоскостей. Видимость плоскостей устанавливают с помощью конкурирующих точек скрещивающихся прямых, принадлежащих этим плоскостям.
Лист 3
Выполнить две задачи на способы преобразования проекций. Пример выполнения листа представлен на рисунке 2.
Основная надпись по форме 4 (рис. 52).
Задача 1. Дано: треугольник АВС. Требуется: способом вращения вокруг осей, перпендикулярных плоскостям проекций, определить натуральную величину треугольника АВС. Данные для выполнения задачи берут из таблицы 2.

Рисунок 2 - Образец выполнения листа 2
Указания к выполнению задачи 1 (рис. 2). Соблюдая правила вращения геометрических фигур вокруг оси, перпендикулярной плоскости проекции, необходимо выполнить два действия: 1) привести треугольник АВС в положение проецирующей плоскости, т. е. перпендикулярной плоскости проекций. Признаком перпендикулярности заданной плоскости плоскостям проекций на эпюре является вырождение одной из проекций плоскости треугольника α (А, В, С) в прямую линию. Для получения фронтально-проецирующей плоскости необходимо горизонталь плоскости α (А, В, С) вместе с системой всех точек треугольника АВС поставить в положение, перпендикулярное фронтальной плоскости проекций, а для получения горизонтально-проецирующей плоскости необходимо фронталь плоскости α (А, В, С) со всеми точками плоскости перевести в положение прямой, перпендикулярной горизонтальной плоскости проекций; 2) полученную проецирующую плоскость преобразовать в плоскость уровня, т. е. параллельную либо горизонтальной, либо фронтальной плоскости проекций, в зависимости от ее положения на первом этапе преобразования. Для этого выродившуюся в прямую линию проекцию треугольника АВС изобразить в положении, параллельном оси X. Проекция треугольника АВС на одной из плоскостей проекций и будет являться натуральной величиной треугольника АВС.
Таблица 2
| Номер варианта | Значения координат, мм | ||||||||
| XА | YА | ZA | XB | YB | ZB | XC | YC | ZC | |
Задача 2. Дано: четырехугольник EBCD и точка А. Требуется: способом замены плоскостей проекций определить расстояние от точки А до плоскости α (Е, В, С, D), построить проекции этого расстояния на исходном эпюре.
Точки Е, В, С, D для всех вариантов имеют одинаковые координаты: Е (90, 60, 10), В (60, 90, 80), С (10, 60, 80), D (40, 30, 10). Координаты точки А берут из таблицы 3.
|
|
|
Таблица 3
| Вариант | ||||||||||
| Координаты точек | Значения координат, мм | |||||||||
| XА YA ZA |
Указания к выполнению задачи 2. Соблюдая правила построения геометрических фигур на замененных плоскостях проекций, необходимо: 1) преобразовать плоскость общего положения α (Е, В, С, D) в плоскость фронтально-проецирующую и построить проекцию точки А. Положение новой плоскости определяет новая ось проекций Х', которая должна располагаться перпендикулярно горизонтальной проекции горизонтали плоскости α (Е, В, С, D); 2) определить расстояние от точки А до заданной плоскости. Оно равно отрезку перпендикуляра АК, опущенного из точки А на плоскость α (Е, В, С, D), выродившуюся на новой фронтальной плоскости проекций в прямую линию; 3) получив основание перпендикуляра (К2'), построить его проекции на исходном чертеже задачи. Так как проекция отрезка A2'K2' перпендикуляра b – натуральная величина отрезка, то, следовательно, его проекция на плоскость П1 будет параллельна оси Х'. Координату Z для построения фронтальной проекции точки К (К2) следует взять с плоскости проекций П2'.
Лист 4
Выполнить две задачи на пересечение многогранных поверхностей и определение натуральной величины сечения многогранника плоскостью. Пример выполнения листа приведен на рисунке 3.
Основная надпись по форме 4 (рис. 52).
Задача 1. Дано: прямая четырехгранная пирамида и трехгранная горизонтальная призма. Требуется: вычертить три проекции пирамиды и призмы, построить линию пересечения этих многогранников и определить ее видимость. Для всех вариантов стороны основания пирамиды Р1F1 = К1Е1 = 60 мм; К1Р1 = Е1F1 = 70 мм; высота пирамиды 110 мм; высота вертикальной грани призмы 90 мм; длина всех ребер призмы 140 мм (рис. 3). Угол α равен углу между стороной основания пирамиды КР и фронтальной плоскостью проекций. Величины l, h, a, а также значения координат точек Р и D берут из таблицы 4 в соответствии с номером варианта.
Указания к выполнению задачи 1. Вычерчивание пирамиды нужно начинать с точки Р, а призмы – с точки D. Основание пирамиды расположено в плоскости П1, ее ребра прямые общего положения, одна из граней призмы – фронтальная плоскость (параллельная П2), две других – профильно-проецирующие, поэтому ребра этих граней на плоскости П3
проецируются в точки.
Линия пересечения многогранников определяется по точкам пересечения ребер каждого из них с гранями другого многогранника или построением линий пересечения граней многогранников. Соединяя каждые пары точек одних и тех же граней отрезками прямых, получаем линии пересечения многогранников. Видимыми линиями пересечения многогранников будут те, которые принадлежат их видимым граням. Линия пересечения многогранников строится только с использованием фронтальных и горизонтальных проекций фигур. Профильные проекции фигур применить для проверки правильности определения точек пересечения ребер с гранями и их последовательного соединения.
Задача 2. Дано: прямая четырехгранная пирамида и одна грань призмы. Требуется: способом плоскопараллельного перемещения определить натуральную величину сечения пирамиды с гранью призмы. Исходные данные берут из таблицы 4.
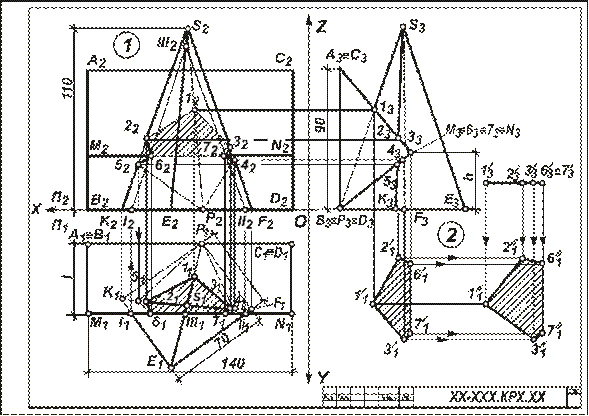
Рисунок 3 - Образец выполнения листа 4
Таблица 4
| Координаты точек | ХXP | YP | XZP | ХXD | YD | XZD | 7l | h | Угол α, 0 | Секущая грань |
| Номера вариантов | Значения координат, мм | |||||||||
| ACNM BDNM ACNM BDNM BDNM ACNM BDNM ACNM BDNM ACNM |
Указания к выполнению задачи 2. Для выполнения данной задачи используют результат решения задачи 1, выделяя из него часть линии пересечения, которая относится к указанной для варианта грани по таблице 4. Профильную проекцию пирамиды с заданной секущей гранью призмы принимают за фронтальную проекцию и к ней достраивают горизонтальную проекцию сечения пирамиды гранью по уже имеющейся горизонтальной проекции в задаче 1, но соответственно развернув его в проекционной связи (рис. 3). Так как секущая грань занимает положение проецирующей плоскости, то, для того, чтобы получить натуральную величину сечения, достаточно произвести одно перемещение. Способом плоскопараллельного перемещения проецирующую плоскость грани ставим в положение плоскости уровня (параллельное горизонтальной плоскости проекций).
При способе плоскопараллельного перемещения все точки фигуры перемещаются в плоскостях, параллельных какой-либо одной плоскости проекций. Поэтому проекции траекторий точек на вторую плоскость проекций представляют собой прямые линии, параллельные оси проекций. Как и при вращении, вокруг осей, перпендикулярных плоскостям проекций, при плоскопараллельном перемещении одна проекция фигуры не меняется ни по величине, ни по форме.
Лист 5
Выполнить три задачи на пересечение поверхности плоскостью и прямой. Пример выполнения листа на рисунке 4. Задачи 1 и 2 выполняют в левой части листа, одна под другой, а задачу 3 – в правой части листа.
Основная надпись по форме 4 (рис. 52).
Задача 1. Дано: пирамида и прямая l. Требуется: определить точки пересечения прямой l с поверхностью трехгранной пирамиды. Все варианты задач имеют два одинаковых параметра: высоту пирамиды 70 мм и диаметр вспомогательной окружности 60 мм, в которую вписывается треугольное основание произвольного расположения по усмотрению студента. Положение прямой общего положения, которая пересекает пирамиду, устанавливается студентом также самостоятельно.
Указания к выполнению задачи 1. Чтобы решить задачу, необходимо: 1) заключить прямую во вспомогательную плоскость частного положения (фронтально-проецирующую или горизонтально-проецирующую); 2) построить линию пересечения пирамиды с этой вспомогательной плоскостью; 3) отметить точки пересечения проекций прямой с проекциями линии пересечения; 4) определить видимость.
Так как плоскость, в которую заключается прямая, частного положения, то одна из проекций фигуры сечения пирамиды совпадает с проекцией секущей плоскости, выродившейся в линию. Вторую проекцию сечения достраивают по точкам фигуры сечения, которые лежат непосредственно на ребрах. Задача может иметь одно из трех решений:
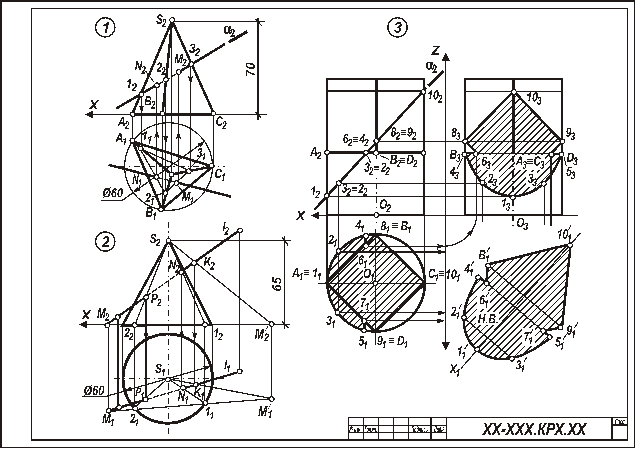
Рисунок 4 - Образец выполнения листа 5
прямая пересекает пирамиду в двух точках, в одной точке (касается) и не пересекает поверхность.
Задача 2. Дано: основание конуса— окружность диаметра 60 мм, высота конуса 70 мм и прямая l. Требуется: определить точки пересечения прямой l с поверхностью прямого кругового конуса. Положение прямой студент выбирает самостоятельно, учитывая характеристику прямой, указанную в таблице 5.
Указания к выполнению задачи 2 (рис. 4). Чтобы решить задачу, необходимо выполнить действия, аналогичные перечисленным в указаниях к задаче 1. При этом следует напомнить, что выбирать нужно такие вспомогательные секущие плоскости, которые дают наипростейший контур сечения конуса: окружность и треугольник. Так, например, для задачи 2, помещенной на рисунке 4, вспомогательная секущая плоскость является плоскостью общего положения, которая проходит через вершину конуса и задана двумя пересекающимися прямыми (заданной прямой и произвольной прямой, проходящей через вершину конуса и точку K данной прямой). Такая плоскость дает сечение в виде треугольника. Если через горизонтальную прямую провести горизонтальную плоскость, сечение будет иметь форму окружности. После определения точек пересечения прямой с конусом следует установить видимые отрезки прямой.
Таблица 5
| Номер варианта | Характеристика прямой l |
| Нисходящая общего положения Фронтальная под углом к П1 - 450 Горизонтально-проецирующая Горизонтальная под углом к П2 - 300 Фронтально-проецирующая Восходящая общего положения Горизонтальная под углом к П2 - 450 Фронтально-проецирующая Фронтальная под углом к П1 - 300 Горизонтально-проецирующая |
Задача 3. Построить три проекции линии пересечения сложной поверхности с фронтально-проецирующей плоскостью и, используя один из способов преобразования чертежа, определить натуральную величину этого сечения. Данные для вычерчивания комбинированной поверхности берут из рисунка 5.
Указания к выполнению задачи 3. Задачу размещают на правой стороне листа (рис. 4). Высота всей комбинированной поверхности равна 100 мм, нижняя ее часть — 35 мм. Размеры диаметров оснований поверхностей и вспомогательных окружностей, а также стороны многоугольников приведены на рисунке 5. Положение секущей плоскости для своего варианта студент назначает самостоятельно. Задачу решают в два этапа: 1) строят проекции сечения; 2) определяют натуральную величину сечения.
Так как в данном задании для пересечения предложена плоскость частного положения – фронтально-проецирующая, то решение задачи сводится к построению проекций ряда точек фигуры сечения заданной поверхности как точек, расположенных на образующих или направляющих линиях этой поверхности. Первоначально крайние и промежуточные точки сечения назначаются на следе секущей плоскости. Натуральную величину сечения определяют по тем же точкам, которые были установлены на первом этапе. За ось вращения плоскости сечения выбирают фронталь плоскости сечения, совпадающую с его осью симметрии. Для того чтобы избежать наложения изображений, фронталь следует размещать на свободном поле чертежа, параллельно следу секущей плоскости. Каждая точка сечения будет вращаться: вокруг оси в плоскости, перпендикулярной ей. Радиус вращения отображен в натуральную величину на горизонтальной плоскости проекций и соответствует расстоянию от точки до продольной оси симметрии (оси вращения).
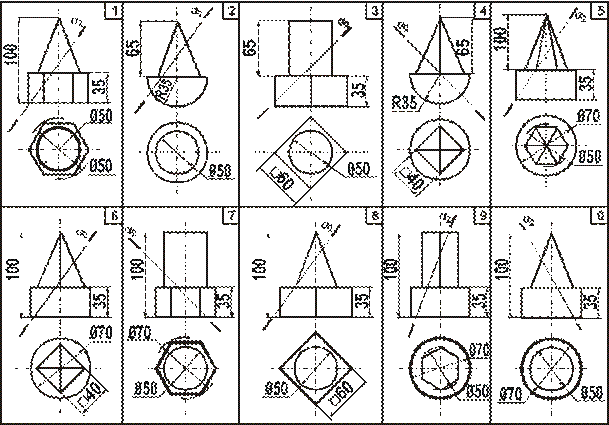
Рисунок 5 - Данные задачи 3, лист 5
Лист 6
Выполнить две задачи на пересечение многогранных и кривых поверхностей и построение разверток поверхностей. Пример выполнения см. на рисунке 6.
Основная надпись по форме 4 (рис. 52).
Задача 1. Дано: многогранник и кривая поверхность. Требуется: способом вспомогательных секущих плоскостей построить линию пересечения многогранной и кривой поверхностей, выделив ее видимые и невидимые участки. Данные для задачи приведены на рисунке 7.
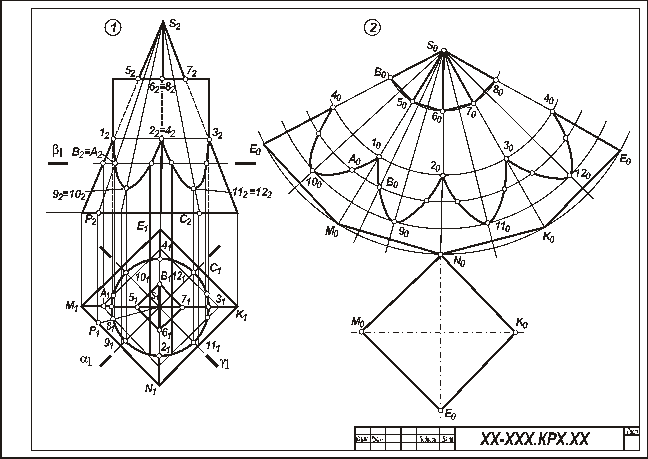
Рисунок 6 - Образец выполнения листа 6
Указания к выполнению задачи 1. Задачу выполняют на левой половине листа в такой последовательности: 1) намечают расположение вспомогательных секущих плоскостей частного положения (уровня) или проецирующих; 2) с их помощью определяют характерные и промежуточные точки линии пересечения поверхностей; 3) полученные точки соединяют плавными кривыми или прямыми линиями, установив предварительно последовательность расположения точек на линии пересечения поверхностей. Видимую часть линий контура, в том числе и линии пересечения, обводят сплошной основной, а невидимую – штриховой линиями.
Задача 2. Дано: две пересекающиеся поверхности – многогранник и кривая поверхность – и линия их пересечения. Требуется: построить полную развертку одной из пересекающихся поверхностей и нанести на нею линию их пересечения. Поверхность для построения развертки студент выбирает сам из двух поверхностей задачи 1 в соответствии со своим вариантом. Линия пересечения поверхностей наносится по результату решения задачи 1.
Указания к выполнению задачи 2 (рис. 6). Задачу выполняют на правой половине листа в такой последовательности; 1) в кривую поверхность вписывают многогранник; 2) определяют натуральные величины всех ребер вписанного многогранника; 3) на плоскости чертежа строят одну из граней поверхности по ее натуральным величинам ребер и к ней последовательно пристраивают остальные грани, пользуясь смежными ребрами; 4) соответствующие вершины граней соединяют плавными кривыми линиями. При развертывании многогранной поверхности выполняют только вторую и третью операции. Линия пересечения поверхностей наносится на развертку с помощью ее характерных точек. Для каждой такой точки в ортогональных проекциях определяют положение образующей и направляющей линий поверхности, на пересечении которых расположена взятая точка. Строят эти линии (образующую и направляющую) на развертке и в их пересечении отмечают искомую точку линии пересечения поверхностей (рис. 6).

Рисунок 7 - Данные задачи 1, листа 6
Лист 7
Выполнить две задачи на построение линии пересечения поверхностей различными способами. Пример выполнения листа представлен на рисунке 8. Основная надпись по форме 4 (рис. 52).
Задача 1. Дано: две пересекающиеся кривые поверхности. Требуется: способом вспомогательных секущих плоскостей построить линию их пересечения, выделив ее видимые и невидимые участки. Данные варианта задачи берут по рисунку 9.
Указания к выполнению задачи 1. Задачу выполняют с левой стороны листа в такой последовательности: 1) определяют опорные точки (точки пересечения очерковых образующих поверхностей; наивысшие и наинизшие точки линии пересечения; точки, определяющие границы видимости); 3) определяют промежуточные точки линии пересечения; 4) все найденные точки пересечения последовательно соединяют кривой линией, учитывая их видимость.
При выборе вспомогательных секущих плоскостей необходимо помнить, что они должны пересечь одновременно обе поверхности и дать наипростейшие фигуры сечения. Для всех вариантов заданий вспомогательными секущими плоскостями могут быть выбраны плоскости уровня: для одних — горизонтальные, для других — вертикальные или те и другие. Точками пересечения поверхностей являются точки пересечения контуров фигур сечения поверхностей, лежащих в одной и той же вспомогательной секущей плоскости. Каждая секущая плоскость может определить от одной до четырех точек линий пересечения в зависимости от характера пересекающихся поверхностей, их расположения относительно друг друга и положения самой секущей плоскости.

Рисунок 8 - Образец выполнения листа 7
Задача 2. Дано: две пересекающиеся поверхности вращения. Требуется: способом секущих концентрических сфер построить линию их пересечения и определить ее видимость. Данные варианта задачи берут по рисунку 10.

Рисунок 9 - Данные задачи 1, лист 7

Рисунок 10 - Данные задачи 2, лист 7
Указания к выполнению задачи 2. Задачу выполняют в правой половине листа в следующем порядке: 1) определяют центр концентрических сфер – точку пересечения осей поверхностей вращения – и проводят ряд концентрических окружностей – сфер различного радиуса, диапазон радиусов сфер определяется минимальным и максимальным радиусами. Минимальный радиус секущей сферы назначается из условия касания сферы одной и пересечения другой пересекающихся поверхностей. Максимальным радиусом является отрезок прямой от центра сферы до наиболее удаленной точки пересечения очерков пересекающихся поверхностей (Ф21 и Ф22 на рисунке 11,а); 2) строят линии пересечения выбранных сфер с заданными пересекающимися поверхностями. Каждая из сфер, будучи соосной с заданными поверхностями, пересечет их по окружностям, которые в данной задаче на плоскости П2 представляют собой прямые линии – хорды окружности, называемые параллелями (рисунок 11,б). Точки пересечения проекций полученных параллелей являются проекциями искомых точек линии пересечения поверхностей; 3) найденные точки пересечения поверхностей соединяют плавной кривой линией; 4) достраивают горизонтальную проекцию линии пересечения по имеющимся точкам.
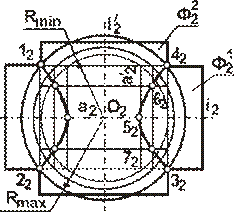
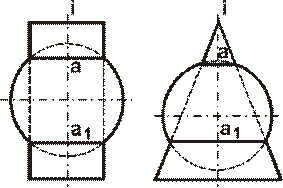
а) б)
Рисунок 11
Лист 8
Выполнить четыре задачи на построение аксонометрических проекций плоских и пространственных фигур. Пример исполнения листа приведен на рисунке 12. Расположение элементов задач с их построением и обозначением выполнить в соответствии с примером. Разбивку поля чертежа для отдельных задач выдержать согласно размерам рисунка 12, но линии границ не наносить.
Основная надпись по форме 4 (рис. 52).
Задача 1. Дано: ортогональные проекции трех правильных шестиугольников, принадлежащих плоскостям проекций П1, П2, П3 (рисунок 12, задача 1, изображения а, б, в). Требуется: построить их аксонометрические проекции в прямоугольной изометрии. Описанные окружности для построения правильных шестиугольников имеют диаметр 40 мм.
Указания к выполнению задачи 1. Задачу выполняют в такой последовательности: 1) строят проекции трех правильных шестиугольников, которые расположены в плоскостях проекций П1, П2, П3 (рис. 12, задача 1, изображения а, б, в): 2) наносят оси координат, соответствующие прямоугольной изометрической проекций, и, используя приведенные коэффициенты искажения, намечают вершины шестиугольников по соответствующим аксонометрическим осям координат, которые затем соединяют линиями. При выполнении данной задачи следует помнить, что в прямоугольной изометрии угол между проецирующим лучом и плоскостью аксонометрических проекций равен 90°, аксонометрические оси координат располагают под углом 120° (рис. 12), действительные коэффициенты искажения по всем осям равны 0,82, но для практических построений применяют приведенные коэффициенты искажения, равные 1. При приведенных коэффициентах прямоугольная изометрия увеличивается в 1,22 раза (1:0,82=1,22), а прямоугольная диметрия – в 1,06 раза (1: 0,94=1,06).
Задача 2. Дано: ортогональные проекции трех окружностей соответственно принадлежащих плоскостям проекций П1, П2, П3 (см. рисунок 12, задача 2, изображения а, б, в). Требуется: построить их аксонометрические проекции в прямоугольной диметрии. Диаметр окружностей равен 40 мм.
Указания к выполнению задачи 2. Задачу выполняют в нижней левой части листа в следующем порядке: 1) строят ортогональные проекции окружностей и намечают на них характерные точки, соответственно расположенные в плоскостях проекций П1, П2, П3 (см. рисунок 12, задача 2, изображения а, б, в); 2) наносят аксонометрические оси координат, соответствующие прямоугольной диметрической проекции, и, используя приведенные коэффициенты искажения, строят выбранные характерные точки окружностей, а также большую ось эллипса АВ и малую ось эллипса CD. Схема расположения осей и приведенные коэффициенты искажений изображены на рисунке 14. Тут же на схеме указаны углы аксонометрических осей для их построения. Окружности в аксонометрии проецируются в виде эллипсов, причем при использовании действительных коэффициентов искажения большая ось эллипса равна диаметру окружности (рис. 16). Так как приведенные коэффициенты аксонометрическое изображение увеличивают, то, следовательно, большая и малая оси тоже увеличиваются. В таблице 6 приведены значения осей эллипсов для различных положений окружностей и видов аксонометрии. При построении аксонометрии окружности нужно помнить, что во всех трех плоскостях прямоугольной изометрической и диметрической проекций большая ось эллипса должна быть направлена перпендикулярно оси, которая отсутствует в этой плоскости, а малая ось сохраняет направление отсутствующей в этой плоскости оси.
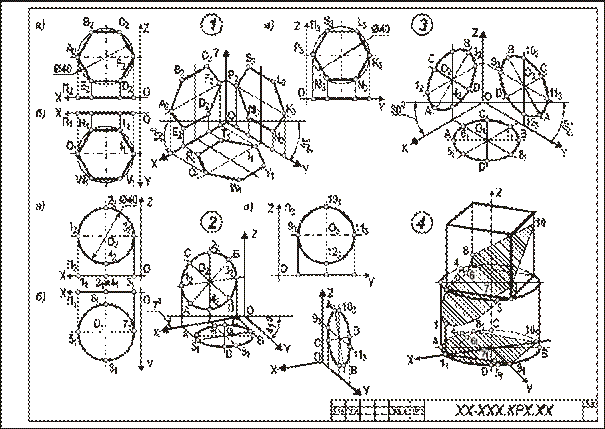
Рисунок 12 - Образец выполнения листа 8
Таблица 6
| Оси эллипса | Прямоугольная изометрия | Прямоугольная диметрия | ||||||||||
| К=0,82 | К=1 | К=0,94 | К=1 | |||||||||
| xOy | xOz | yOz | xOy | xOz | yOz | xOy | xOz | yOz | xOy | xOz | yOz | |
| Большая ось | D | D | D | 1,22D | 1,22D | 1,22D | D | D | D | 1,06D | 1,06D | 1,06D |
| Малая ось | 0,58 | 0,58 | 0,58 | 0,71 | 0,71 | 0,71 | 0,33 | 0,88 | 0,33 | 0,35 | 0,94 | 0,35 |
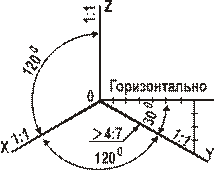

Рисунок 13 Рисунок 14
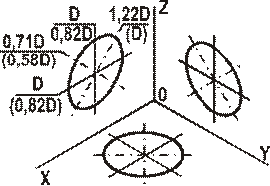

Рисунок 15 Рисунок 16
Задача 3. Дано: ортогональные проекции трех окружностей, соответственно принадлежащих плоскостям проекций П1, П2, П3 (см. рисунок 12, задача 3). Требуется: построить их аксонометрические проекции в прямоугольной изометрии. Диаметр окружностей равен 40 мм.
Указания к выполнению задачи 3. Для решения задачи используют ортогональные проекции окружностей, которые присутствуют в условии задачи 2 листа 8. Последовательность выполнения задачи 3 полностью соответствует порядку решения задачи 2 этого же листа. Коэффициент искажения по осям указан на рисунке 13, большие и малые оси эллипсов – в таблице 8, а их изображение приведено на рисунке 15.
Задача 4. Дано: ортогональные проекции комбинированной поверхности и сечение этой поверхности фронтально-проецирующей плоскостью. Требуется: построить прямоугольную изометрию или прямоугольную диметрию комбинированной поверхности вместе с контуром сечения этой поверхности плоскостью. За исходные данные для построения аксонометрии комбинированной поверхности берут ортогональные проекции задачи 3 листа 5 (см. рис. 4) и найденное на них сечение от фронтально-проецирующей плоскости. Вид аксонометрии студент определяет сам.
Указания к выполнению задачи 4 (рис. 12). Задачу выполняют в нижней правой части листа в такой последовательности: 1) на ортогональном чертеже наносят оси прямоугольной системы координат, к которой относят заданную поверхность; 2) выбирают вид аксонометрии с таким расчетом, чтобы обеспечить наилучшую наглядность поверхности, и наносят аксонометрические оси координат; 3) в системе координат X0У строят вторичные проекции оснований поверхностей и сечения; 4) каждую точку вторичной проекции поднимают на высоту ее положения, которое она занимает в натуре, и по этим точкам строят аксонометрическое изображение.
В процессе выполнения любой аксонометрии следует запомнить, что выполнение аксонометрии нужно начинать со вторичной проекции, т. е. с построения аксонометрии плоской фигуры, являющейся видом данного предмета сверху или спереди. Поэтому для выполнения листа 8 первые три задачи были на построение плоских фигур.
|
|
|


