Определение внутренних силовых факторов. Метод сечения

Реферат

 

1. Виды нагрузок, типы опор и балок

 

Для того чтобы судить о прочности исследуемого тела, находящегося в равновесии под действием внешних сил, прежде всего необходимо уметь определить вызванные ими внутренние усилия.

Внешние силы деформируют тело; внутренние усилия сопротивляясь этой деформации, стремятся сохранить первоначальную форму и объем тела.

Обнаружение внутренних усилий, их вычисление составляют первую и основную задачу сопротивления материалов, которая решается с помощью МЕТОДА СЕЧЕНИЙ, сущность этого метода заключается в следующем:

первая операция. Рассекаем (мысленно) стержень по сечению в котором следует определить величину внутренних усилий (см. рис.1а).

вторая операция. Отбрасываем какую-либо часть стержня, например, часть 1 (рис. 1б). Обычно отбрасывают ту часть, к которой приложено большее число сил.

третья операция. Заменяем силы, действующие на оставшуюся часть главным вектором 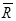 и главным моментом 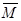, совместив центр приведения О с центром тяжести (ц.т.) сечения (на рис.1,б М не показан).

четвертая операция. Уравновешиваем оставшуюся часть, так как до рассечения она находилась в равновесии. Для этого в точке О прикладываем силу R и момент M (на рис. не показан), равные и противоположно направленные главному вектору 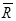 и главному моменту 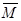. Усилия  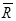и и 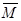являются теми внутренними усилиями, которые передавались со стороны отброшенной на оставшуюся часть стержня.

Метод сечений является лишь первым шагом по пути исследования внутренних сил, так как с его помощью не удается выяснить закон распределения внутренних сил в сечении.

Составляя уравнения равновесия для отсечённой части тела, можно получить проекции на координатные оси как главного вектора, так и главного момента (см. рис.1)

 

Рис.1

 

При расчёте брусьев начало координат помещают в центре тяжести рассматриваемого поперечного сечения его. Ось "Z" в прямом брусе совмещают с его продольной осью, в кривом - направляют по касательной к его оси в точке, где помещено начало координат.

Оси "X" и "Y" совмещают с направлениями главных центральных осей инерции рассматриваемого сечения. Проекции на координатные оси главного вектора и главного момента внутренних сил в брусе обозначают соответственно: , , 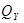N, Mx, My, и называют внутренними силовыми факторами (внутренними усилиями).

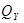, - представляют собой поперечные силы в направлении оси "X" или "Y" (Н)- нормальную (продольную) силу (н.)., My - изгибающие моменты относительно осей соответственно "X" или "Y" (нм)- крутящий момент (нм).

Рассмотрев отсечённую часть бруса (например правую) (рис.1,б) и составив на основании метода сечений уравнения равновесия, можно сказать следующее:

нормальная сила N есть сила внутренняя, численно равная сумма проекции на продольную ось бруса всех внешних сил, расположенных по одну сторону от рассматриваемого сечения.

-поперечная сила в направлении оси "X" численно равна сумме проекций на ось "X" всех внешних сил, расположенных по одну сторону от рассматриваемого сечения.

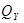- поперечная сила в направлении оси "Y" численно равна сумме проекций на ось "Y" всех внешних сил, расположенных по одну сторону от рассматриваемого сечения- изгибающий момент относительно оси "X" численно равна сумме моментов всех внешних сил, расположенных по одну сторону от этого сечения.- изгибающий момент относительно оси "Y" численно равна сумме моментов всех внешних сил, расположенных по одну сторону от этого сечения.- изгибающий момент относительно оси "Z" численно равна сумме моментов всех внешних сил, расположенных по одну сторону от этого сечения.

Итак, в общем случае нагружения бруса внутренние силы в его поперечных сечениях приводятся к указанным шести внутренним силовым факторам.

Всякий стержень, работающий на изгиб, называется балкой.

Внешними силами, вызывающими изгиб балок, являются активные нагрузки и реакции опор (рис.2).

 

Рис. 2

 

Активные силы полагаются известными и сводятся к сосредоточенным силам F(H), парам сил m (нм) и распределенным по длине балки нагрузкам q (н/м). Величина и направление реакций R1,R2 определяются из условия равновесия балки и вида её опорных закреплений.

Балки могут иметь следующие три типа опор:

. Жёсткое защемление или заделка. Конец балки лишён трёх степеней свободы. Он не может перемещаться ни в вертикальном, ни в горизонтальном направлениях и не имеет возможности поворачиваться. Следовательно, в этой опоре возникают три реакции: две силы R1 и R2, препятствующие линейным смещениям конца балки и один реактивный момент MR, препятствующий повороту. На рис.3 показанное схематическое устройство и условное обозначение жёсткого защемления.

 

Рис. 3

2. Шарнирно-неподвижная опора

 

Такая опора лишает балку двух степеней свободы: вертикального и горизонтального смещений, но не препятствует вращению балки вокруг шарнира. Следовательно, в данной опоре возникают две составляющие опорной реакции R1 и R2. Схематическое устройство и условное обозначение опоры дано на рис. 4.

 

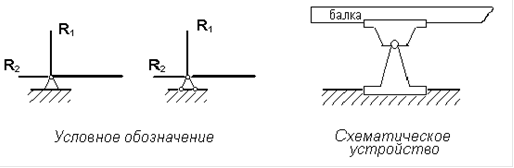
Рис. 4

 

. Шарнирно-подвижная опора - это наименее жёсткое опирание, она лишает конец балки только одной степени свободы - вертикального линейного перемещения. В шарнирно-подвижной опоре возникает одна реакция.

На рис.5 представлено схематическое устройство и условное обозначение опоры.

 

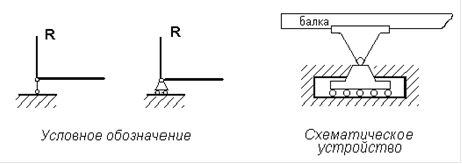
Рис. 5

Следует обратить внимание на то, что данная опора препятствует перемещению конца балки как вниз, так и вверх. Необходимо заметить, что на практике плоскость катания подвижной опоры всегда делают параллельной оси балки. Тогда реакция подвижной опоры должна иметь направление перпендикулярное к оси балки.

Применяя разные виды опор, получаем различные типы балок. Так как балка в плоскости имеет три степени свободы, то для неподвижного закрепления балку необходимо лишить всех трёх степеней свободы.

Первый тип балки - консоль (рис. 6,а). Консоль имеет на одном конце заделку, отнимающую все три степени свободы, а другой её конец свободный. В заделке возникают: реактивный момент, вертикальная реакция и при наличии горизонтальной или наклонной нагрузки, горизонтальная реакция. Консоль применяется в технике в виде кронштейнов, мачт и т.д.

Второй тип балки - двухопорная балка (рис. 6,б). Опирание балки в двух точках осуществляется применением одной подвижной и одной неподвижной шарнирных опор, в совокупности отнимающих у балки все три степени свободы. В подвижной опоре возникает только вертикальная реакция, в неподвижной - вертикальная и горизонтальная (при наличии горизонтальных составляющих нагрузок).

Расстояния между опорами называется пролётом. Если одна из опор смещена на некоторое расстояние, то балка называется одноконсольной (рис. 6,в). Если же обе опоры смещены, то балка называется - двухконсольной (рис. 6,г).

Балки перечисляемых типов имеют минимально необходимое число опор, в связи с этим они статически определимы, т.е. их опорные реакции могут быть найдены из уравнения равновесия.

Постановка дополнительных опор делает балку статически неопределимой: расчёт таких балок возможен лишь с учётом их деформаций.

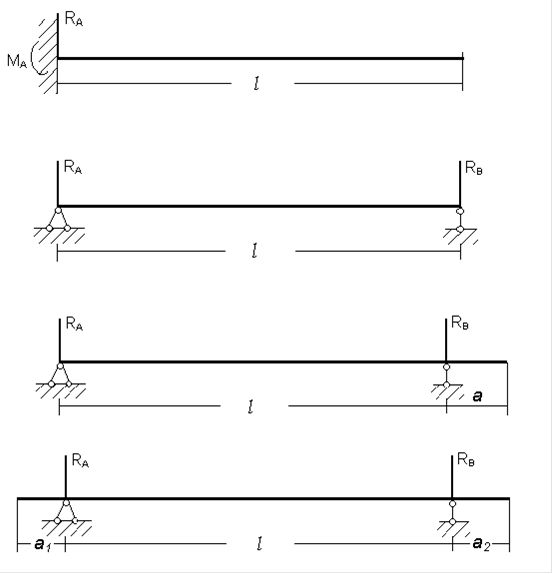
Рис. 6

 

. Растяжение-сжатие прямого бруса

 

Под растяжением или сжатием понимается такой вид нагружения, при котором в поперечных сечениях бруса возникают только нормальные силы (N), а все прочие внутренние силовые факторы равны нулю. Растягивающие нормальные силы (т.е. силы, направленные от поперечного сечения рис. 7.а) принято считать положительными, а сжимающие силы (т.е. силы направленные к поперечному сечению рис.7,б) - отрицательными. Этим правилом пользуемся при построении эпюр продольных сил.

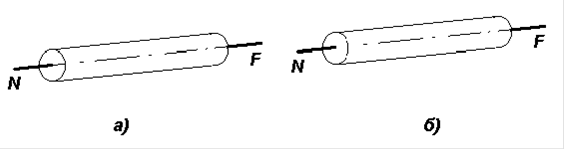
Рис.7

 

Пример 1. Для бруса, находящегося в равновесии и нагруженного так, как показано на рис.8 а построить эпюру нормальных сил N. Разбиваем брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы.участок - СД, II участок - ВС, III участок - ВА.

Применяя метод сечений, оставляем правую и отбрасываем левую часть бруса: это позволяет не определять опорной реакции. Проводя произвольное сечение I-I на участке I и составляя для части бруса (рис. 8,б) уравнение равновесия SZ=0, получим F-N=0, N=F

Очевидно, что все сечения на участке I равноценны. Таким образом, на участке I брус растянут силой F. Построим эпюру нормальных сил (рис.8,д). От нулевой линии, параллельной оси бруса, отложим вверх в масштабе на участке I ординаты, равные F и эпюру пометим знаком (+).

Проделаем подобные операции для участка II. Рассечём брус сечением 2-2 и рассмотрим правую отсечённую часть (рис.8,в)

 

SZ=0 F+2F-N2=0 N2=3F

 

На эпюре нормальных сил на участке II отложим ординаты, равные 3F в том же масштабе, что и на участке I. Аналогично определяем нормальную силу на участке III. Проводим сечение 3-3 (рис. 8,в) и пишем уравнение равновесия SZ=0

F+2F-4F+N3=0 N3=F

 

Рис. 8

 

Усилие N3 направлено к сечению, т.е. сжимает участок III. Откладываем вниз от нулевой линии ординаты, равные F и ставим знак (-) на эпюре N (рис.8,д)

Таким образом, на рис.8,д построена эпюра нормальных сил для заданного бруса; Эпюры силовых факторов штрихуются линиями, перпендикулярными оси, т.к. они являются графиками, построенными в масштабе, т.е. каждая штриховая линия представляет собой продольную силу возникающую в соответствующем поперечном сечении.

Пример 2. Брус длиною 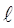 нагружен равномерно распределённой нагрузкой с интенсивностью q(кн/см) и сосредоточенной силой F приложенной на свободном торце и равной (кн) (рис.9а). Построить эпюру нормальных сил.

Для определения нормальных сил применим метод сечений. Рассечём брус на расстоянии Z от свободного торца. Отбросим верхнюю часть, а для нижней части бруса составим уравнение равновесия (рис.9,б)

Предположим, что сила N направлена вверх SZ=0

 

N-qZ+ =0 N=qZ- ()

 

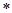из уравнения видно, что нормальная сила N меняется по длине бруса по линейному закону. Для построения эпюры находим значения силы в крайних сечениях: при Z=0 и при Z=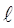

 

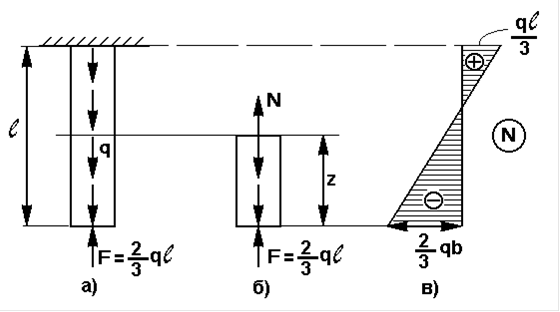
Рис. 9

 

Подставим эти значения Z в уравнение (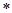) и получим:

при Z=0 N= , т.е. внутренняя нормальная сила оказалась сжимающей:

при Z= 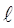N= , нормальная сила стала растягивающей. Эпюра показана на рис.9,в

Самая большая нормальная сила N= возникает на свободном торце бруса. Следовательно, это сечение самое опасное.

В местах приложения сосредоточенных сил на эпюре получаются скачки, равные величине этих сил. Следует отметить, что при определении внутренних силовых факторов можно говорить только о сечениях, удалённых от мест приложения нагрузки. Сила не может быть строго сосредоточенной в одной точке. Передача нагрузки всегда совершается по некоторой площадке, в пределах которой внутренняя сила распределяется по некоторому закону, изучение которого выходит за рамки курса "Сопротивление материалов". Таким образом, эпюра в областях приложения сосредоточенной нагрузки условна.

 

. Изгиб прямого бруса

 

Под изгибом понимается такой вид нагружения, при котором в поперечных сечениях бруса возникают изгибающие моменты. Если изгибающий момент в сечении является единственным силовым фактором, то изгиб называется чистым. Если наряду с изгибающим моментом в поперечных сечениях бруса возникают и поперечные силы, то изгиб называется поперечным.

Предполагается, что изгибающий момент и поперечная сила лежат в одной из главных плоскостей бруса (примем, что эта плоскость ZOY). Такой изгиб называется плоским.

Во всех рассматриваемых ниже случаях имеет место плоский поперечный изгиб балок.

Для расчета балки на прочность или жесткость необходимо знать внутренние силовые факторы, возникающие в ее сечениях. С этой целью строятся эпюры поперечных сил (эпюра Q) и изгибающих моментов (М).

При изгибе прямолинейная ось бруса искривляется, нейтральная ось проходит через центр тяжести сечения. Для определенности при построении эпюр поперечных сил и изгибающих моментов установим для них правила знаков. Примем, что изгибающий момент будет считаться положительным, если элемент бруса изгибается выпуклостью вниз (рис.10.а), т.е. таким образом, что его сжатые волокна находятся в верхней части.

Если момент изгибает брус выпуклостью вверх, то этот момент будет считаться отрицательным (рис.10.б).

Положительные значения изгибающих моментов при построении эпюры откладываются, как обычно в направлении оси У, что соответствует построению эпюры на сжатом волокне.

 

Рис. 10

 

Поэтому правило знаков для эпюры изгибающих моментов можно сформулировать следующим образом:

ординаты моментов откладываются со стороны слоев бруса.

Изгибающий момент в сечении равен сумме моментов относительно этого сечения всех сил, расположенных по одну стороны (любую) от сечения.

Для определения поперечных сил (Q) установим правило знаков: поперечная сила считается положительной, если внешняя сила стремиться повернуть отсеченную часть балки по час. стрелке относительно точки оси, которая соответствует проведенному сечению (рис.11,а). Отрицательная сила показана на рис. 11, б.

 

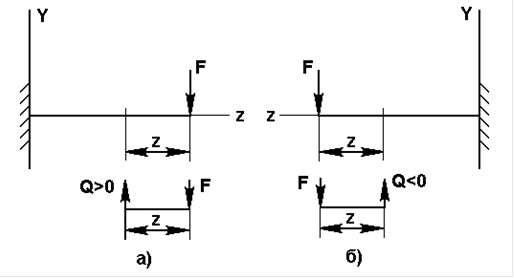
Рис. 11

 

Поперечная сила (Q) в произвольном поперечном сечении бруса численно равна сумме проекций на ось ОУ внешних сил, приложенных к его осеченной части.

Рассмотрим несколько примеров построения эпюр поперечных сил и изгибающих моментов. Все силы перпендикулярны оси балок, поэтому горизонтальная составляющая реакции равна нулю. Деформированная ось балки и силы лежат в главной плоскости ZOY.

Пример 3.

Балка длиной  защемлена левым концом и нагружена сосредоточенной силой F и моментом m=2F (рис. 12,а).

Построим эпюры поперечных сил Q и изгибающих моментов Миз.

В нашем случае на балку с правой стороны не наложено связей. Поэтому чтобы не определять опорные реакции, целесообразно рассматривать равновесие правой отсеченной части балка. Заданная балка имеет два участка нагружения. Границы участков-сечения, в которых приложены внешние силы. 1 участок - СВ, 2 - ВА.

 

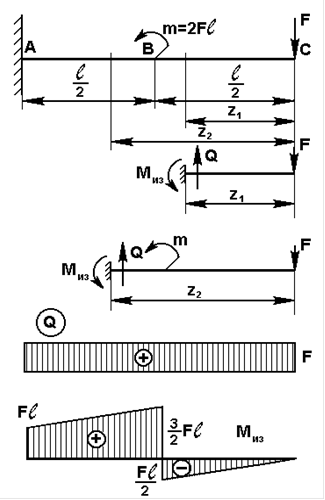
Рис. 12

Проводим произвольное сечение на участке 1 и рассмотрим равновесие правой отсеченной части длиною Z1.

(рис.12,б). Из условия равновесия следует: Q=F; Миз= -FZ1 ()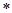

Поперечная сила положительна, т.к. внешняя сила F стремится повернуть отсеченную часть по часовой стрелке. Момент изгибающий считается отрицательным, т.к. он изгибает рассматриваемую часть балки выпуклостью вверх.

При составлении уравнений равновесия мысленно закрепляем место сечения, как это показано на рис.12 б, в; из уравнений (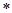) следует, что поперечная сила на I участке от Z1 не зависит и является постоянной величиной. Положительную силу Q=F откладываем в масштабе вверх от осевой линии балки (рис.12, г), перпендикулярно к ней.

Изгибающий момент зависит от Z1.

 

При Z1=O Миз=O при Z1= 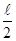Миз=

 

Полученное значение (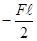) откладываем вниз, т.е. эпюра Миз строится на сжатом волокне (рис.12, д).

Переходим ко второму участку (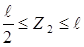). Рассекаем участок II на произвольном расстоянии Z2 от свободного правого торца балки (рис.12,а) и рассматриваем равновесие отсеченной части длиною Z2 (рис.12,в). Изменение поперечной силы и изгибающего момента на основе условий равновесия можно выразить следующими уравнениями:

=F Mиз= - FZ2+2F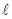

Величина и знак поперечной силы не изменились. Эпюра поперечной силы представлена на (рис.12,г).

Величина изгибающего момента зависит от Z2.

 

При Z2= Mиз= 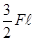, при Z2=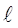

 

Изгибающий момент получился положительным, как в начале участка II, так и в конце его. На участке II балка изгибается выпуклостью вниз.

 

Рис. 13

 

Откладываем в масштабе величины моментов вверх по осевой линии балки (т.е. эпюра строится на сжатом волокне). Эпюра Миз показана на (рис.12, д). Наибольший изгибающий момент возникает в сечении, где приложен внешний момент m и по абсолютной величине равен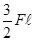

Заметим, что на длине балки, где Q сохраняет постоянную величину, изгибающий момент Миз меняется линейно и представляется на эпюре наклонными прямыми. Из эпюр Q и Миз видно, что в сечении, где приложена внешняя поперечная сила, эпюра Q имеет скачок на величину этой силы, а эпюра Миз - излом. В сечении, где приложен внешний изгибающий момент, эпюра Миз имеет скачок на величину этого момента. На эпюре Q это не отражается. Из эпюры Миз видим, что max Миз= 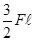, следовательно, опасное сечение предельно приближено с левой стороны к т.В (рис.12, д).

Пример 4

Для балки изображенной на рис.13,а, построить эпюры поперечных сил и изгибающих моментов. На длине  балка нагружена равномерно распределенной нагрузкой с интенсивностью q(КН/см).

На опоре А (шарнир неподвижный) возникнет вертикальная реакция Ra (горизонтальная реакция равна нулю), а на опоре В (подвижный шарнир) возникает вертикальная реакция Rв.

Определим вертикальные реакции опор, составляя уравнение моментов относительно опор А и В.

 

SMA=0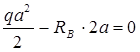

 

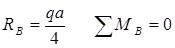
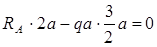
Проверим правильность определения реакции:

SY=0

 

т.е. опорные реакции определены правильно.

Заданная балка имеет два участка нагружения: I участок - АС.участок - СВ.

На первом участке 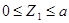 a, в текущем сечении Z1 (рис.13,а) из условия равновесия отсеченной части имеем

 

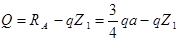
При . При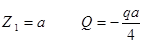

 

Эпюра Q имеет вид наклонной прямой, пересекающей ось Z (рис.13.б).

Уравнение изгибающих моментов на 1 участке балки:

 

 

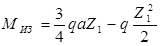
Момент от реакции Ra изгибает балку на участке 1, выпуклостью вниз, поэтому изгибающий момент от реакции Ra вводится в уравнение со знаком плюс. Нагрузка qZ1 изгибает балку выпуклостью вверх, поэтому момент от нее вводится в уравнение со знаком минус. Изгибающий момент изменяется по закону квадратной параболы.

Поэтому, необходимо выяснить имеет ли место экстремум. Между поперечной силой Q и изгибающим моментом существует дифференциальная зависимость на анализе которой мы остановимся далее

Как известно, функция имеет экстремум там, где производная равна нулю. Следовательно, чтобы определить при каком значении Z1, изгибающий момент будет экстремальным, надо уравнение поперечной силы приравнять к нулю.

 

 

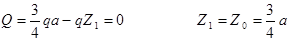
Так как поперечная сила меняет в данном сечении знак с плюса на минус, то изгибающий момент в этом сечении будет максимальным. Если Q меняет знак с минуса на плюс, то изгибающий момент в этом сечении будет минимальным.

Итак, изгибающий момент при 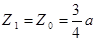 , является максимальным.

Поэтому, строим параболу по трем точкам (рис.13,в)

При Z1=0 Миз=0

 

При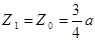

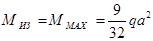
При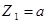

 

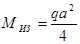
Рассекаем второй участок на расстоянии Z2 от опоры В (рис.13,а) Из условия равновесия правой отсеченной части балки имеем:

 

 

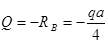
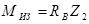
При  величина Q=const,

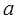
изгибающий момент будет:

при , при 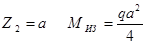 , т.е. MИЗ меняется по линейному закону.

Эпюра поперечных сил представлена на рис.13,б изгибающих моментов на рис.13,в. Примерный вид изогнутой оси балки предоставлен пунктиром на рис.13,а.

Пример 5.

Балка на двух опорах, имеющая пролет равный 2 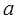и левую консоль длиною 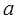, нагружена так, как показано на рис.14,а., где q(Кн/см) - погонная нагрузка. Опора А-шарнирно неподвижна, опора В - подвижный каток. Построить эпюры Q и Миз.

Решение задачи следует начинать с определения реакций опор. Из условия равенства нулю суммы проекций всех сил на ось Z следует, что горизонтальная составляющая реакции на опоре А равна 0.

 

 откуда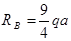

 

Для проверки используем уравнение

 

 

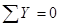
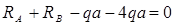
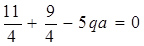
Уравнение равновесия удовлетворяются, следовательно, реакции вычислены правильно. Переходим к определению внутренних силовых факторов. Заданная балка имеет три участка нагружения:

участок - СА,

участок - АД,

участок - ДВ.

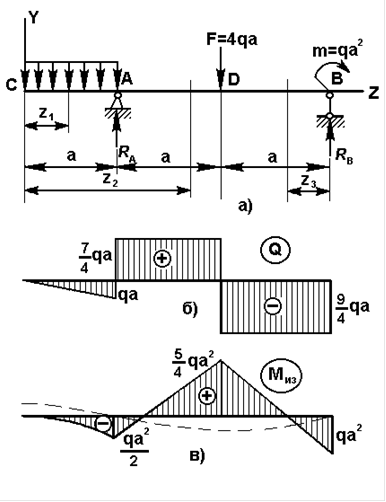
Рис. 14

 

Рассечем 1 участок на расстояние Z1 от левого торца балки (рис.14.а).

при Z1=0 Q=0 МИЗ=0

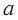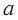при Z1= Q= -q МИЗ=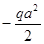

Таким образом, на эпюре поперечных сил получается наклонная прямая, а на эпюре изгибающих моментов - парабола, вершина которой находится на левом конце балки рис.14,в.

На участке II (a £ Z2 £2a) для определения внутренних силовых факторов рассмотрим равновесие левой отсеченной части балки длиною Z2. Из условия равновесия имеем:

Поперечная сила на этом участке постоянна.

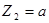
При  , при

На участке III () Q=RB

Полная эпюра поперечных сил для всей балки имеет вид, представленный на рис.14.б. А на рис.14.в представлена полная эпюра изгибающих моментов и пунктиром показан примерный вид изогнутой оси балки рис.14.а.

Из эпюры видим, что наибольший изгибающий момент возникает в сечении под силой F и равен 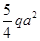. Это сечение будет самым опасным.

На эпюре Миз имеется скачок на опоре В, равный внешнему моменту, приложенному в данном сечении.

Рассматривая построеные выше эпюры, нетрудно подметить определенную закономерную связь между эпюрами изгибающих моментов и эпюрами поперечных сил. Докажем это.

Пусть балка загружена произвольной распределенной нагрузкой (рис.15,а).

Выделим элемент длиной dZ и в проведенных сечениях приложим моменты и поперечные силы (рис.15,а). В пределах малого участка dZ нагрузку можно считать распределенной равномерно.

Приравнивая нулю сумму проекций всех сил на вертикальную ось и сумму моментов относительно поперечной оси С (рис.15,б)

Рис. 15

 

 

Производная от поперечной силы по длине бруса равняется по модулю интенсивности нагрузки.

 

 

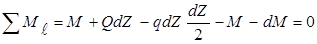
Отбрасывая величину высшего порядка малости получим:

 

 

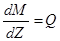
т.е. поперечная сила является производной от изгибающего момента по длине бруса.

Учитывая полученные дифференциальные зависимости можно сделать общие выводы. Если брус нагружен равномерно распределенной нагрузкой интенсивности q=const, очевидно, функция Q будет линейной, а Миз - квадратичной. Это можно было наблюдать на примере эпюр, показанных на рис.13 (1 участок).

Если брус нагружен сосредоточенными силами или моментами, то в промежутках между точками их приложения интенсивность q=0. Следовательно, Q=const, а Миз является линейной функцией Z. В точках приложения сосредоточенных сил эпюра Q претерпевает скачок на величину внешней силы, а в эпюре Миз возникает соответствующий излом (разрыв в производной).

В месте приложения внешнего изгибающего момента наблюдается разрыв в эпюре моментов, равный по величине приложенному моменту.

Если Q>0, то Миз растет, а если Q<0, то Миз убывает.

Дифференциальные зависимости используются для проверки уравнений составленных для построения эпюр Q и Миз, а также для уточнения вида этих эпюр.

Изгибающий момент меняется по закону параболы, выпуклость которой всегда направлена навстречу внешней нагрузки.

 

. Плоские статистические определяемые рамы

 

Рамой называется конструкция, состоящая из прямолинейных (реже криволинейных) стержней, которые, как правило, жестко связаны между собой.

Различают плоские, плоскопространственные и пространственные рамы.

У плоских рам, которые будут рассматриваться в этом разделе, оси всех стержней и нагрузки лежат в одной плоскости. Реакции связей, наложенные на плоские рамы, лежат, естественно, в той же плоскости.

Используя метод сечений, из уравнений равновесия легко установить, что в поперечных сечениях плоских рам, несущих нагрузки, действующие в их плоскостях, могут возникнуть внутренние силовые факторы, лежащие в плоскости рамы, а именно:

нормальная сила N,

поперечная сила Q,

изгибающий момент Миз.

В рассмотренных ниже примерах ординаты эпюр изгибающих моментов отложены на сжатом волокне брусьев. Используя это условие можно не ставить знаков на эпюре изгибающих моментов. Правила знаков, принятые для балки, в принципе сохраняются. Эпюры поперечных сил имеет, вообще говоря, второстепенное значение.

Нормальные силы следует исследовать только в тех элементах конструкций, которые не изгибаются

 

 

Пример 6.

Для рамы предоставленной на рис.16 построить эпюры поперечных сил и изгибающих моментов.

В статически определимых жестких рамах, заделанных одним концом, предварительное определение опорных реакций необязательно. Построение эпюр в таких случаях можно вести от свободного конца. Рама имеет четыре участка, для каждого из них составляем уравнение поперечных сил и изгибающих моментов, соблюдая принятые ранее правила знаков.

 

 

. участок: рассекаем участок на расстояние Z1 от свободного торца E (рис.16,а).

Ординаты изгибающего момента откладываем на сжатом волокне бруса, а знак момента указывать не будем.

2. участок:  Q=0 МИЗ=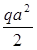

. Участок: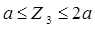

 

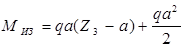
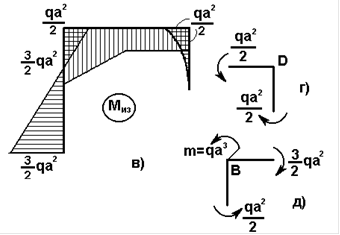
Оба изгибающих момента берем с одним знаком, т.к. сжимают одно и то же (нижнее) волокно.

 

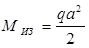
. участок:

 

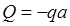
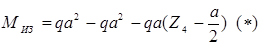
В этом уравнении для Миз со знаком плюс взят момент, сжимающий правое волокно (момент от сосредоточенной силы F), а моменты, сжимающие левое волокно бруса, взяты со знаком минус. Разумеется, что эпюра Миз не изменится, если знаки изгибающих моментов в уравнении (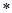) поменять на противоположные.

 

 

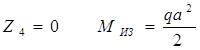
Получаем момент со знаком плюс, т.е. сжато будет правое волокно бруса.

 

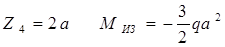 (сжато левое волокно бруса)

 

Окончательный вид эпюр Q и Миз представлен соответственно на рис.16, б и в.

Для проверки правильности построения эпюры Миз, можно использовать следующие положения: любой узел, вырезанный из наружной рамы, должен находиться в равновесии под действием моментов, заменяющих действие на него отброшенных элементов.

Так, например, вырежем узел D рассмотренной рамы (рис.16.г)

Запишем уравнение: SМD=0

Вырежем узел B (рис.16.д): SМв=0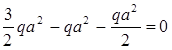

Таким образом, условия равновесия узлов Д и В удовлетворяются. Сечение А самое опасное, т.к. в нем возникает самый большой Миз.

 

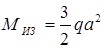 (рис.16,в)

 

Пример 7.

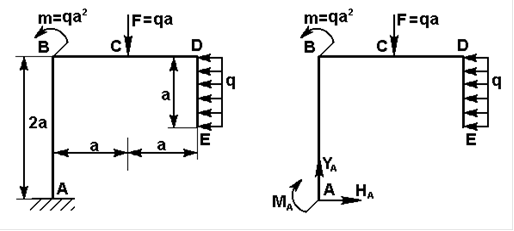
Построить эпюры поперечных сил и изгибающих моментов для рамы, представленной на рис.17,а. Для решения задачи необходимо предварительно, используя уравнение равновесия статистики, определить опорные реакции:

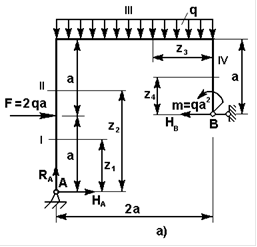
Рис. 16

 

 

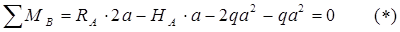
Спроектируем все силы на горизонтальную ось:

 

 

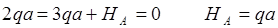
Из уравнения (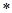) получим: Ra=2qa

 

 

Для проверки запишем сумму проекций на вертикальную ось:

 

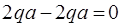
т.е. реакции определены правильно.

Переходим к построению эпюр.

Рама имеет четыре участка нагружения.

участок: 0£ Z1£a.

Рассмотрим равновесие отсеченной части длиной Z1. Из условия равновесия следует: Q=-Hа= -qa

Миз=HaZ1,

при Z1=0 Миз=0,

при Z1= 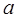Миз=

 

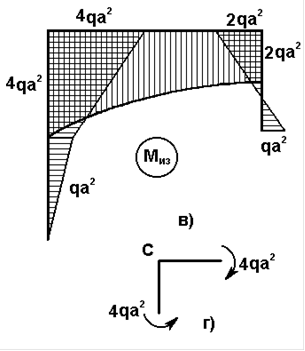
Рис. 17

 

Сжатое волокно на 1 участке - правое, поэтому строим эпюру на правом волокне 1 - го учатска рамы.

участок: a£Z2£2a.

рассмотрим равновесие отсеченной части длиною Z2.

Q=-Ha-F=-qa-2qa=-3qa

Миз=HaZ2+F(Z2-a)

В уравнении изгибающие моменты записаны с одинаковым знаком, т.к. оба момента сжимают правое волокно рамы.

При Z2=а Миз=qa2

При Z2=2a Миз=4qa2

участок: 0£Z3£2a

Рассмотрим равновесие части рамы, расположенной справа от сечения.

 

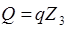
при

при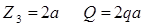

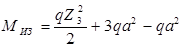
при

при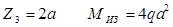

 

Обе ординаты изгибающих моментов откладываем вниз от осевой линии рамы, т.к. сжатыми оказались нижние волокна рамы.

Изгибающий момент меняется по закону квадратной параболы. Парабола обращения выпуклостью вверх.

участок: 0£Z4£2a

Рассмотрим равновесие участка рамы длиною Z4=Hв=3qa МИЗ=HвZ1-m=3qaZ4-qa2,

при Z4=0 MИЗ= -qa2 этот момент сжимает правые волокна, поэтому откладываем ординату на правом волокне,

при Z4=a МИЗ=2qa2 этот момент сжимает левое волокно, поэтому на эпюре Миз ордината 2qa2 откладывается на левом волокне.

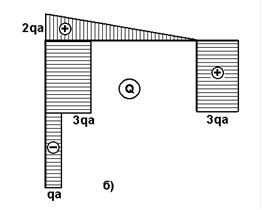
Эпюры Q и МИЗ показаны на рис.17,б,в.

Построеные эпюры всегда следует проверять с точки зрения соблюдения дифференциальных зависимостей между q, Q и МИЗ. Кроме того, следует проверять, соблюдается ли равновесие в узлах рамы. Например, вырезая узел С, прикладываем к вырезанной части внутренние силовые факторы рис.17,г, возникающие в указанных сечениях.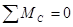

 

 

Если к рассматриваему узлу приложен внешний момент, то этот момент должен войти в уравнение равновесия рассматриваемого узла. Опасное сечение С, где

Рассмотрим особенности построения эпюр внутренних силовых факторов для пространственных рам. Ограничимся построением эпюры одних моментов

Поделиться:

Воспользуйтесь поиском по сайту: