Обработка результатов прямых измерений

 

1) Производят измерения физической величины n раз (серию измерений):

А ₁, А ₂,… А _n (n = 3-5) затем находят среднее значение измеряемой величины

2) Находят абсолютную случайную погрешность каждого измерения:

, , .

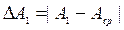Окончательное значение случайной погрешности принимают равным максимальному ее значению в серии измерений.

Принимая во внимание то, каким прибором проводилось измерение, находят приборную погрешность Δ А _приб.

Окончательное (результирующее) значение абсолютной погрешности:

 

.

 

Если Δ А _случ >> Δ А _приб, то Δ А = Δ А _случ, и в дальнейших расчетах учитывается только случайная погрешность.

Если Δ А _случ << Δ А _приб, то Δ А = Δ А _приб, и в дальнейших расчетах учитывается только приборная погрешность.

 

Окончательный результат записывается в виде:

 

А = (А _изм ± Δ А) (размерность измеряемой величины).

Обработка результатов косвенных измерений

 

Пусть физическая величина А связана с несколькими величинами x ₁, x ₂… x_n некоторой функциональной зависимостью A = f (x ₁, x ₂… x_n), например, R = U / I, R = ρℓ / S и т.д.

Среди величин x ₁, x ₂… x_n могут содержаться прямо измеряемые величины, а также заранее известные табличные величины, данные установки. Пусть в результате обработки всех величин, найдены их средние значения x _1ср, x _2ср… x_{n ср} и абсолютные погрешности Δ x ₁, Δ x ₂… Δ x_n. Тогда результат для косвенно измеряемой величины получают по следующей схеме:

1) среднее значение рассчитывают по формуле:

A = f (x _1ср, x _2ср… x_{n ср});

2) по виду функциональной зависимости находят относительную погрешность с помощью логарифмического дифференциала:

После нахождения значения ε_А находят абсолютную погрешность Δ А:

Δ А = А _ср·ε_А.

Окончательный результат записывают в виде:

А = (А _ср ± Δ А) (размерность).

Примеры нахождения ε для наиболее простых функций:

Функция	Относительная погрешность

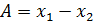
Следует обратить внимание на то, что погрешности всегда складываются.

 

В расчетных формулах часто встречаются величины, взятые из таблицы (π, е т.п.).

В значении универсальной постоянной, например, числа π, надо взять столько значащих цифр, чтобы относительная погрешность этой постоянной (ε_π) была на порядок (в 10 раз) меньше, чем суммарная относительная погрешность измеренных величин, тогда ε_π не будет заметно увеличивать результирующую погрешность.

Например, π ≈ 3,14159. Пусть ε = 1%, тогда если взять π = 3,1, то погрешность округления Δπ = 3,1415–3,1 = 0,04 и

ε_π = Δπ/π = 0,04/3,1 = 0,013 = 1,3%.

В этом случае ε_π ~ ε и к результирующей погрешности добавляется 1,3% «из ничего»!

Если же взять π = 3,14, то Δπ = 3,1415–3.14 = 0,002. Тогда относительная погрешность округления числа π составляет ε_π = Δπ/π = 0,002/3,14 = 0,1%, т.е. на порядок меньше погрешности измерения, и почти не влияет на общую погрешность.

Такие же рассуждения следует применять для величин, значения которых берутся в справочных таблицах, а также для иррациональных чисел, входящих в формулы.

Если в значении величин, заданных на установках не указаны абсолютные погрешности, то считается, что они измерены с точностью равной половине единицы последнего указанного разряда:

m = 8 г → Δ m = 0,5 г;

m = 8,3 г →Δ m = 0,05 г.

 

Окончательная запись результатов измерений:

1) Округление результатов рекомендуется начать с округления абсолютной погрешности: в погрешности оставляют одну значащую цифру; если же старшая значащая цифра погрешности 1 или 2, то рекомендуется округлять погрешность до двух цифр.

 

2) Окончательный результат измерений А_ср округляют или уточняют «до погрешности»: последняя значащая цифра в результате находится в том же разряде, что и в погрешности.

3) Окончательно имеем: А = (А _изм ± Δ А) ед.

 

12	Поделиться:

Воспользуйтесь поиском по сайту: