Сведем данные для расчета в таблицу

Таблица расчета данных.

Обозн. размера	Размер, мм	xj	Есj	Тj	aj	ajTj/2	Есj+ajTj/2	xj(Ес j+ajTj /2)	½xj½Tj	(½xj½Tj)2
А1	20JS12 (±0,105)	–1		0,105					0,105	0,011
А2	54h12 (-0,3)	+1	–0,15	0,3	+0,2	0,03	–0,12	–0,12	0,3	0,09
А3	100h12 (-0.35)	+1	–0,175	0,35	+0,2	0,035	-0,14	-0,14	0,35	0,1225
А4	20JS12 (±0,105)	–1		0,105					0,105	0,011
А5	114h12 (-0.41)	–1	-1,1	0,41	+0,2	0,041	-1,1	+1,1	0,41	0,168

 

1. Номинальное значение замыкающего размера

N_D=

N_D= –20 +54+100 –20 –114 = 0.

2. Среднее отклонение замыкающего размера:

Е_сr =-0,12-0,14+1,1= +0,84.

3. Допуск замыкающего размера:

Допуски на составляющие размеры можно оставить без изменения.

4. Предельные отклонения замыкающего размера:

А_rmax =N_r + Ec_r + 0,5×T_r= 0+ 0,84 + 0,5×0,8= 1,24 мм;

А_rmin = N_r + Ec_r – 0,5×T_r= 0 + 0,84 – 0,5×0,8= 0,44 мм

5. Сравниваем полученные результаты с заданными:

А_{r max расч.} =1,24 А_{rmax зад.} = 1,2

А_{rmin расч.} = 0,44 А_rminзад. = 0,4

Следовательно, изменения предельных отклонений составляющих размеров не требуется.

3 ОБРАБОТКА РЕЗУЛЬТАТОВ ПРЯМЫХ МНОГОКРАТНЫХ РАВНОТОЧНЫХ ИЗМЕРЕНИЙ

 

 

В таблице 2.1 приведены 100 независимых числовых значений результата измерений напряжения U цифровым вольтметром, каждое из которых повторилось m раз. Определить значение измеряемого напряжения.

Таблица 2.1

Исходные данные, В
U	25,11	25,12	25,14	25,15	25,16	25,17	25,18	25,20	25,21
m
U	25,22	25,23	25,24	25,25	25,26	25,27	25,28	25,29	25,30
m
U	25,31	25,32	25,33	25,34	25,35	25,36	25,37	25,38	25,39
m
U	25,40	25,41	25,42	25,43	25,45	25,46	25,48	25,49	25,54
m

 

 

Решение:

1 Используя полученные данные, найдем значение среднего арифметического и оценки среднего квадратического отклонения S_u:

В; В.

2 С помощью правила «трех сигм» проверим наличие грубых промахов:

В

В

Ни один из результатов не выходит за границы интервала , следовательно, с вероятностью 0,9973 принимается гипотеза об отсутствии грубых промахов.

3 Предположим, что вероятность результата измерений подчиняется нормальному закону. Проверим правдивость этой гипотезы с помощью критерия Пирсона. Все расчеты сведем в таблицу 2.2.

4 Определим значение аргумента интегральной функции нормированного нормального распределения:

(см. формулу 2.14)

Таблица 2.2

Расчет критерия Пирсона

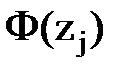
i	Интервалы					mj – nPj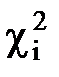
	–¥	25,11		-2,16778	0,0113	0,0223	-0,23	1,17967E-05
	25,11	25,145		-1,77889	0,0375	0,0262	-0,62	0,000100713
	25,145	25,18		-1,39	0,0694	0,0319	0,81	0,000209296
	25,18	25,215		-1,00111	0,1401	0,0707	-2,07	0,003029424
	25,215	25,25		-0,61222	0,2483	0,1082	8,18	0,072399217
	25,25	25,285		-0,22333	0,3897	0,1414	-2,14	0,006475554
	25,285	25,32		0,165556	0,5398	0,1501	0,99	0,00147113
	25,32	25,355		0,554444	0,6915	0,1517	-2,17	0,007143401
	25,355	25,39		0,943333	0,8159	0,1244	-2,44	0,007406278
	25,39	25,425		1,332222	0,9032	0,0873	-0,73	0,000465222
	25,425	25,46		1,721111	0,9554	0,0522	-1,22	0,000776945
	25,46	+¥		+¥		0,0446	0,54	0,000130054

a. Поскольку конец предыдущего интервала является одновременно началом следующего, то теоретическая вероятность попадания результата определится по формуле (2.13). Началом первого интервала следует считать «–¥», а функции .

b. По последнему столбцу рассчитаем значение -критерия:

.

c. Определим табличное (критическое) значение -критерия Пирсона, задавшись доверительной вероятностью, равной 0,95 и вычислив по формуле (2.12) число степеней свободы:

r = 12 – 3 = 9

; .

Таким образом, с вероятностью 0,99 гипотеза о нормальности закона распределения вероятности результата измерений напряжения принимается.

5 Представим результаты в виде доверительного интервала с доверительной вероятностью Р = 0,99.

a. Для этого определим среднее квадратическое отклонение среднего арифметического 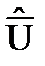значения напряжения по формуле (2.3):

В

b. Исходя из того, что закон распределения вероятности результата измерения с вероятностью 0,99 соответствует нормальному, считаем, что, и закон распределения вероятности среднего арифметического тоже соответствует нормальному. Поэтому выбираем параметр t по таблице нормированного нормального распределения вероятности. Для доверительной вероятности Р=0,99 параметр t=3.

Тогда результат измерения запишется следующим образом:

или с вероятностью .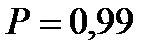

25,2781 В ≤ U ≤ 25,3321 В

Учитывая то обстоятельство, что среднее квадратическое отклонение 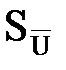может быть оценено экспериментально с точностью до двух значащих цифр, округлим границы доверительного интервала до тысячных долей вольта. В итоге получим:

8,601 В ≤ U ≤ 8,655 В

Если же есть основания полагать, что среднее арифметическое имеет неизвестное, отличное от нормального распределение вероятности, то относительную ширину доверительного интервала рассчитаем по формуле (2.18):

, .

Окончательно результат измерения примет вид (см. формулу (2.17)):

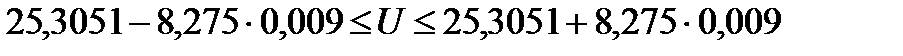
или с вероятностью

или после округления

6 Строим саму гистограмму (рис.2.1).

 

Рисунок 2.1. Гистограмма и выравнивающая нормальная кривая, иллюстрирующая гипотезу о виде ЗРВ

 

 

 

СПИСОК ЛИТЕРАТУРЫ

1. Метрология, стандартизация и сертификация: учебное пособие/В.М.Бастраков.- Йошкар-Ола: Марийский государственный технический университет, 2007.-300с.

2. Димов Ю.В. Метрология, стандартизация и сертификация: Учебник для Вузов-2-е изд.-СПб.:Питер, 2004.-432 с.; ил.

3. Крылова Г.Д. Основы стандартизации, сертификации, метрологии: Учебник для Вузов.-М.: Аудит, ЮНИТИ, 2001.-711 с.

4. Радкевич Я.М. Метрология, стандартизации и сертификация: Учебник для вузов/ Я.М.радкевич, А.Г.Схиртладзе, Б.И.Лактионов.- М.: Высш.шк., 2004.- 767 с.

5. Сергеев А.Г., Латышев М.В., Терегеря В.В. Метрология, стандартизация, сертификация. Учебное пособие. М., 2001-536 с.

6. Шишкин И.Ф. Основы метрологии, стандартизации и контроля качества: Учебн. пособие. - М.: Изд-во стандартов, 1988.

7. Допуски и посадки: Справочник. В 2-х ч. / В.Д. Мягков, М.А. Палей, А.Б. Романов, В.А. Брагинский. 6-е изд., перераб. и доп. – Л.: Машиностроение. Ленингр. отд-ние, 1982.

 

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: