 |
Граф-дерево, граф-лес, определения. Центры дерева. Цикломатическое число графа. Остов графа, хорда графа. Двудольные графы. Задача о назначениях
|
|
|
|
Пути и связность в неориентированных графах. Расстояния между вершинами. Диаметр, радиус, центр графа.
Путь -это последовательность ребер,в кот все ребра различные.
Граф называется связным, если для любойпары различных вершин существует соединяющий их путь.Произвольный граф разбивается на некоторое число связных графов,которые называются компонентами связности.
Минимальным из длин простых цепей,связывающих вершины неординарного графа называется расстоянием.
Центр -это вершина,наименее удаленная от всех вершин.
Диаметром графа называется максимальное расстояние.
Радиусом графа наз минимальное расстояние.
18. Ориентированный граф (кратко орграф) — (мульти) граф, рёбрам которого присвоено направление. Направленные рёбра именуются также дугами, а в некоторых источниках (Оре) и просто рёбрами.
Формально, орграф D=(V, E) есть множество E упорядоченных пар вершин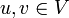 
.
Дуга {u, v} инцидентна вершинам u и v. При этом говорят, что u — начальная вершина дуги, а v — конечная вершина.
Орграф, полученный из простого графа ориентацией ребер, называется направленным. В отличие от последнего, в произвольном простом орграфе две вершины могут соединяться двумя разнонаправленными дугами.
Направленный полный граф называется турниром.
Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам. Ненулевое значение в ячейке матрицы указывает связь между вершиной и ребром (их инцидентность).
В случае ориентированного графа каждому ребру <x,y> ставится в соответствие "-1" на позиции (x,y) и "1" на позиции (y,x); если связи между вершинами нет, то ставится в соответствие "0".
|
|
|
В теории графов изоморфизмом графов 
и 
называется биекция между множествами вершин графов 
такая, что любые две вершины 
и 
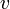графа 
смежны, если и только если вершины 
и 
смежны в графе 
. Здесь графы понимаются неориентированными и не имеющими весов вершин и ребер. В случае, если понятие изоморфизма применяется к ориентированным или взвешенным графам, накладываются дополнительные ограничения на сохранение ориентации дуг и значений весов. Если изоморфизм графов установлен, они называются изоморфными и обозначаются как 
.
Иногда биекция 
записывается в виде подстановки изоморфизма 
..
Отношение изоморфизма графов представляет собой отношение эквивалентности, определенное для графов, и позволяет произвести разбиение исходного класса всех графов наклассы эквивалентности. Множество графов, изоморфных друг другу, называется классом изоморфизма графов (англ.), их число в зависимости от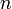 
представляет собой последовательность A000088 в OEIS (1, 1, 2, 4, 11, 34, 156, 1044, 12346,...).
Граф-дерево, граф-лес, определения. Центры дерева. Цикломатическое число графа. Остов графа, хорда графа. Двудольные графы. Задача о назначениях
Деревом называется связанный граф без циклов. Дерево не имеет петель и кратных рёбер. Висячие вершины, за исключением корней, называются листьями. Лес – это граф, компоненты которого являются деревьями. Дерево может быть представлено расслоенным на ярусы (уровни), при этом ветвям, попавшим в один ярус, соответствует одинаковая длина пути исходного графа. Число путей в каждом дереве соответствует числу висячих вершин.
Центр графа –это вершина,наименее удаленная от всех вершин.
Остовное дерево (остов) — это подграф данного графа, содержащий все его вершины и являющийся деревом. Рёбра графа, не входящие в остов, называются хордами графа относительно остова.
|
|
|
Двудо́льный граф — граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части
|
|
|
