Двудольный граф, теорема Кенига о двудольном графе. Хроматическое число графа.

Граф Г=(Х, U) называется двудольным, если имеется разбиение Х=Х ₁È Х ₂ такое, что если (х_i, х_j)Î U, то х_i и х_j принадлежат различным блокам разбиения.

Теорема (Кениг). Граф Г - двудольный Û Г не содержит циклов нечетной длины.

t Пусть Г=(Х, U) – двудольный граф, тогда выполнено разбиение: Х = Y È Z и любой путь С ={(i ₀, i ₁), (i ₁, i ₂),…, (i_{l -1}, i_l)} в соответствии с определением имеет свойство: все вершины с четными номерами принадлежат либо Y, либо Z, тогда все вершины с нечетными номерами принадлежат соответственно либо Z, либо Y. Значит, С – цикл Û i ₀= i_l и длина пути l четная.

Пусть в Г нет циклов нечетной длины. Достаточно доказать, что каждая компонента связности графа Г является двудольной. Пусть Y - множество вершин компоненты связности графа и x Î Y. Определим подмножество Y ¢: Y ¢={ x }È{ y Î Y: r_Г(x, y) – четное}; Y ¢¢= Y \ Y ¢.

Предположим, что в Г имеется ребро (u, w), где u, w Î Y ¢, тогда путь s_{x , u} имеет четную длину, путь s_{u , w} имеет длину 1 и путь s_{w , x} имеет четную длину. Следовательно, цикл, составленный из этих трех путей, имеет нечетную длину, что противоречит исходному предположению. Отсюда Y ¢Ç Y ¢¢=Æ. u

Для графа Г=(Х, U) отображение j: Х ®{1,…, k } называется k – раскрашиванием, если любые две смежные вершины отображаются в разные элементы. Наименьшее k, для которого возможно k –раскрашивание графа, называется хроматическим числом графа. Заметим, что хроматическое число полного n -вершинного графа равно n, двудольного графа - 2.

 

Графы и мультиграфы, ориентированные и неориентированные графы. Степень вершины неориентированного графа. Число n-вершинных неориентированных графов без петель с m ребрами.

Множество Х ={ х ₁, х ₂,...} вкупе с бинарным отношением U на множестве Х называется графом Г(обозначается Г=(Х, U)).

Мультиграфом называют граф с кратными (параллельными) ребрами или дугами, то есть в мультиграфе допускается наличие нескольких ребер или дуг вида (х_i, х_j).

Если элементы каждой пары (х_i, х_j) упорядочены (иначе говоря, бинарное отношение U не симметрично), то Гназывается ориентированным графом или орграфом, а его рёбра называются дугами. В противном случае (когда бинарное отношение U симметрично) граф Гназывается неориентированным.

В неориентированном n -вершинном графе степенью вершины i, обозначаемой deg i, называется число рёбер, инцидентных вершине i.

n вершин, всего ребер С из n по 2= n!/2!(n-2)!

Число графов С из n!/2!(n-2)! по m

 

Граф преобразования конечного множества X. Правило возведения в степень t цикла длины l. Цикловая структура подстановки. Полноцикловая подстановка. Число полноцикловых подстановок степени n.

Графом преобразования g п -множества X называют п -вершинный ориентированный графГ(g) с множеством вершин X и множеством дуг {(x, g (x))}.

Правило возведения цикла Х ¢ преобразования длины l в натуральную степень t: цикл разбивается на d независимых циклов Y ₀¢(t),…, Y_{d -1}¢(t) длины l / d,где d =(t, l), цикл Y_j ¢(t) состоит из элементов g^j (x ₁), g^j+d (x ₁),…, g^{j+i × d} (x ₁),… с точностью до порядка их следования, j =0,…, d -1, и g ⁰(x ₁)= x ₁.

Цикловая структура преобразования g (обозначается С (g)), представляет собой числовую таблицу, в которой указаны длины всех циклов в графе Г(g) и их кратности. Пусть граф Г(g) содержит k_i циклов длины l_i, i =1,…, m, где l ₁<…< l_m, тогда С (g)=(,…, ).

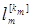Подстановка n -множества называется полноцикловой (п.ц.), если ее граф есть единственный цикл длины n.

Теорема. Число различных п.ц. подстановок n -множества равно (n -1)!.

t Полный цикл элементов n -множества X можно рассматривать как перестановку элементов множества, размещенную на n точках окружности. Значит, число различных полных циклов равно п!. В то же время циклы эквивалентны (реализуют одинаковые п.ц. подстановки) Û отличаются лишь параллельным сдвигом элементов по окружности. Каждый класс эквивалентности состоит из п циклов, тогда число различных п.ц. подстановок п -множества равно (п -1)!. u

Вопросы для подготовки к экзамену

1.Операции над множествами: объединение, пересечение, разность, дополнение, декартово произведение. Булеан конечного множества, его порядок.

2.Частично упорядоченное множество (ч.у.м.). Прямое произведение ч.у.м. Диаграмма ч.у.м. Сравнимые и несравнимые элементы. Цепи и антицепи. Длина и ширина ч.у.м.

3.Определение sup(x,y) и inf(x,y) для элементов x,y ч.у.м. Решетки. Порядок и длина решетки D(n). Порядок, длина и ширина решётки двоичных n-мерных векторов. Бинарное отношение покрытия на ч.у.м. Атомы и коатомы решетки, максимальные и минимальные элементы ч.у.м.

4.Булева функция, ее таблица. Число всех булевых функций от n переменных. Вес булевой функции. Теорема о разложении булевой функции по переменным. Многочлен Жегалкина булевой функции, его степень.

5.Группоид, число различных группоидов порядка n. Полугруппа, моноид. Примеры.

6.Полугруппа, подполугруппа, нуль и идемпотент полугруппы. Моноид, коммутативный моноид. Порядок моноида всех преобразований n-множества.

7.Группа, подгруппа. Аддитивные и мультипликативные группы. Примеры аддитивной и мультипликативной группы.

8.Кольцо, подкольцо, поле, примеры кольца и поля. Операции в кольцах матриц и в кольцах многочленов.

9.Векторное пространство над полем P, базис пространства. Подпространство, линейная оболочка множества векторов. Пример пространства и базиса в нем.

10. Сюръективность, инъективность, биективность функций. Теорема о связи биективности и обратимости функции. Сбалансированность функции.

11. Преобразование множества, ранг и дефект преобразования конечного множества. Неподвижный элемент преобразования множества. Теорема о биективности преобразования конечного множества.

12. Подстановка множества X, инволюция. Степень подстановки. Полная симметрическая группа подстановок S(X), ее порядок при X=n.

13. Число упорядоченных выборок (из n-множества) размера k с возвращением и без возвращения. Формула бинома Ньютона. Свойство симметрии биномиальных коэффициентов. Число неупорядоченных выборок (из n-множества) без возвращения. Свойство суммы биномиальных коэффициентов. свойство суммы четных (нечетных) биномиальных коэффициентов.

14. Разбиения и покрытия конечного множества, продолжение разбиения. Бинарное отношение эквивалентности. Примеры эквивалентности.

15. Формула включения-исключения для порядка объединения k множеств, k4.

16. Существенная переменная булевой функции, равные б.ф. Формула над классом б.ф. ДНФ и КНФ б.ф., СДНФ б.ф. Двойственные и самодвойственные б.ф. Теорема о разложении б.ф. по переменным. Линейная по переменной x1 булева функция f(x1,…,xn).

17. Полнота и замкнутость классов б. ф. Классы Т0, Т1, S, M, A, их порядки. Формулировка критерия Поста полноты системы булевых функций.

18. Множество P2(n) булевых функций от n переменных как векторное пространство. Размерность, примеры базисов в P2(n), пример подпространства.

19. Эксцентриситет вершины графа, радиус, центр и диаметр графа. Теорема об оценке диаметра сильно связного графа.

20. Матрица смежности вершин. Пути и циклы в графе. Связность и сильная связность графа. Теорема о числе путей заданной длины в графе.

21. Изоморфизм графов, объединение графов. Подграф и часть графа. Пример графа и в нем подграфа и части графа.

22. Двудольный граф, теорема Кенига о двудольном графе. Хроматическое число графа.

23. Графы и мультиграфы, ориентированные и неориентированные графы. Степень вершины неориентированного графа. Число n-вершинных неориентированных графов без петель с m ребрами.

24. Граф преобразования конечного множества X. Правило возведения в степень t цикла длины l. Цикловая структура подстановки. Полноцикловая подстановка. Число полноцикловых подстановок степени n.

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: