Амплитудно-импульсная модуляция

Принципы временного разделения каналов

 

Основой построения метода временного разделения каналов является теорема Котельникова, в соответствии с которой непрерывный на интервале 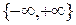первичный сигнал с граничной частотой спектра может быть представлен в форме ряда так называемых отсчетных (базисных) функций 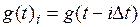, или

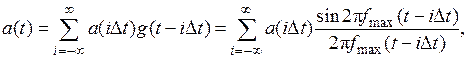(1.1)

где 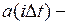отсчеты непрерывного во времени сигнала , взятые в моменты времени ;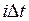

интервал дискретизации непрерывного сигнала .

Частота дискретизации для аналогового сигнала рассчитывается по известным граничным частотам основной части спектра сигнала (f₁ и f₂). Предварительно оценивается относительная ширина полосы спектра сигнала. Если эта полоса меньше одной октавы, то для расчета частоты дискретизации можно пользоваться формулой

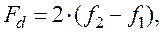
где 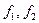- граничные частоты основной части спектра сигнала.

Если относительная полоса больше одной октавы, то для расчета частоты дискретизации можно использовать соотношение

.

 

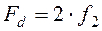Базисные функции 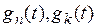ортогональны на бесконечно большом интервале времени, т.е. для них справедливо

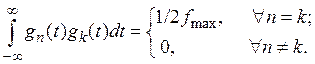
Как следует из (1.1), все сведения о передаваемом первичном сигнале 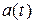содержатся только в отсчетах , а базисные функции для всех одинаковы по форме и отличаются друг от друга только сдвигом во времени, поэтому вместо непрерывного сигнала можно передавать лишь последовательность отсчетов

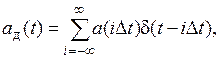(1.2)

(где 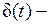дельта-функция), а базисные функции восстанавливать на приеме

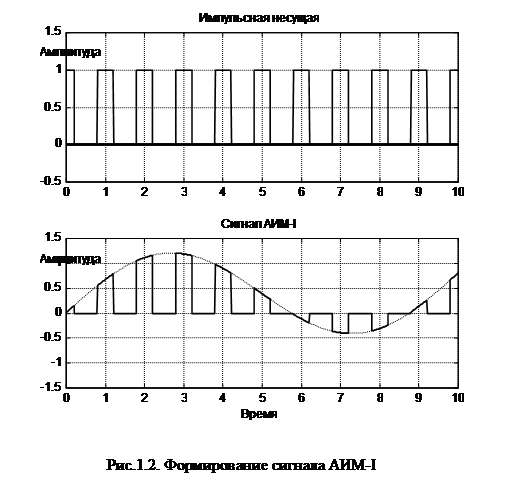
Сформировать последовательность отсчетов практически невозможно, поэтому, реализуя процесс дискретизации, умножают первичный сигнал на периодическую последовательность импульсов (рис.1.2). В этом случае импульсную последовательность следует считать переносчиком или импульсной несущей.

Если периодическая последовательность (импульсная несущая) состоит из импульсов прямоугольной формы одного знака, то она характеризуется параметрами:

- амплитудой ;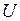

- длительностью (шириной) ;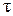

- тактовой частотой ;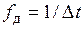

- положением (фазой) импульсов относительно тактовых точек

Отношение 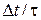называют скважностью импульсной последовательности.

 

Амплитудно-импульсная модуляция

Сигналы амплитудно-импульсной модуляции подразделяются на: АИМ первого рода (АИМ-I, рис.1.2) и АИМ второго рода (АИМ-II, рис.1.3). При АИМ-I мгновенное значение амплитуды импульсов зависит от мгновенного значения модулирующего колебания, а при АИМ-II высота импульсов определяется только значением модулирующего колебания в тактовых точках (в точках дискретизации). Различие между сигналами АИМ-I и АИМ-II оказывается существенным, если длительность импульcов сравнима с их периодом следования.

Формирование сигналов АИМ-I осуществляется с помощью идеального ключа, управляемого последовательностью импульсов (рис.1.1,а).

 

Если коэффициент передачи ключа в открытом состоянии равен единице, а в закрытом–бесконечности, то сигнал АИМ-I можно записать так:

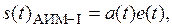
где импульсная несущая с единичной амплитудой.

При этом амплитуды этих импульсов прямо пропорциональны или равны мгновенному значению модулирующего сигнала в точках дискретизации 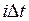. Моменты дискретизации могут совпадать с началом

импульса, его серединой или концом.

Для импульсов прямоугольной формы АИМ-II формируется с помощью схемы рис.1.1,б.

 

В момент появления коротких импульсов последовательности открывается ключ Кл.1, и накопительный конденсатор С заряжается до значения, равного . Это значение напряжения на конденсаторе С остается до прихода импульсов второй последовательности , с помощью которой открывается ключ Кл.2, и через него разряжается конденсатор С.

 

 

τ

Δt

Оба вида сигналов АИМ-I и АИМ-II могут применяться для построения многоканальных систем передачи с временным разделением каналов. Чтобы судить об эффективности использования методов АИМ для организации многоканальной передачи сообщений, необходимо знать полосу частот используемых сигналов.

 

Спектр сигнала АИМ-I

 

Спектр сигнала АИМ-I может быть определен либо с помощью преобразования Фурье, либо с помощью свертки спектров сомножителей:

где спектр первичного сигнала ;

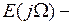спектр импульсной несущей.

Оба эти метода предполагают детерминированность функций или на всем интервале интегрирования.

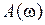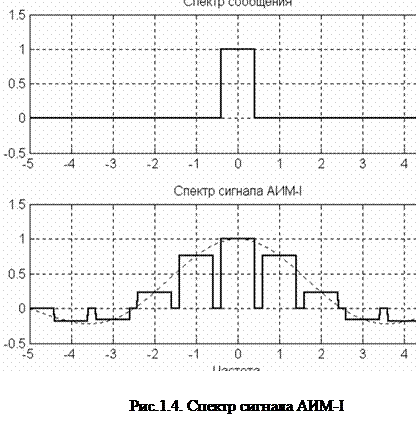
Хотя первичный сигнал является случайной функцией времени, тем не менее, можно положить, что все спектральные составляющие находятся в пределах огибающей (шаблона) спектра . Тогда спектр первичного сигнала имеет вид 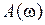(рис.1.4, верхний график).

Импульсная несущая может быть представлена в форме ряда Фурье

Коэффициенты 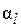ряда Фурье определяются соотношением

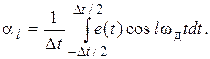
Для импульсной несущей в форме периодической последовательности прямоугольных импульсов длительностью t с единичной амплитудой коэффициенты ряда Фурье

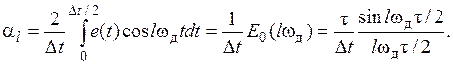
Отсюда следует, что коэффициенты ряда Фурье импульсной несущей при любой форме импульсов с точностью до постоянного множителя численно равны отсчетным значениям спектра 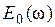одиночного импульса функции . Спектры косинусоид с частотами определяются известным соотношением

.

В соответствии с этим спектр импульсной несущей принимает вид

Откуда спектр сигнала АИМ-I (рис.1.4, нижний график)

. (1.3)

Из этого соотношения следует, что спектр сигнала АИМ-I содержит с точностью до постоянного множителя 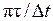спектр модулирующего первичного сигнала и бесконечное множество боковых полос около каждой гармоники импульсной несущей. Следовательно, первичный сигнал можно выделить из сигнала с помощью фильтра нижних частот с граничной частотой полосы пропускания, находящейся в пределах 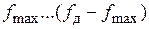. Это будет иметь место только в случае, когда спектр первичного сигнала не перекрывается с нижней боковой полосой колебания частоты 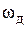, промодулированного первичным сигналом 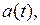поэтому должно выполняться условие .

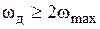Так как , а 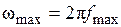, приходим к условию выбора необходимого интервала дискретизации согласно теореме Котельникова, когда 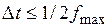. Если же при фиксированной частоте дискретизации оказывается, что 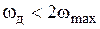, то в полосу частот первичного сигнала будут попадать спектральные составляющие продуктов амплитудной модуляции первой гармоники импульсной несущей и первичного сигнала (рис.1.4). Эти спектральные составляющие на выходе ФНЧ будут создавать помехи дискретизации.

Таким образом, выделение первичного сигнала из сигнала АИМ-I без помех дискретизации возможно только при выполнении условий теоремы Котельникова.

На практике различные первичные сигналы, например разговорные, обладают разной шириной спектра , а частота дискретизации 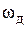выбирается одинаковой. В связи с этим для исключения возможности появления помех дискретизации первичные сигналы вначале ограничиваются по спектру с помощью ФНЧ, а затем производится их дискретизация.

Применительно к организации каналов тональной частоты в системах передачи временного разделения частота дискретизации выбирается равной 8 кГц, а ФНЧ имеет частоту среза 3,4 кГц.

 

Спектр сигнала АИМ-II

 

При определении спектра сигнала АИМ-II воспользуемся вновь соотношением, на основании которого сигнал АИМ-II представим в виде свертки последовательности отсчетов с центральным элементом импульсной несущей , т. е.

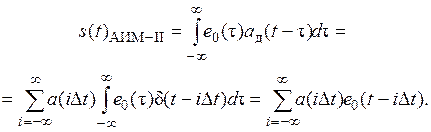
С другой стороны, известно, что свертке во времени функций и 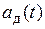в частотной области соответствует произведение спектров исходных сигналов

,

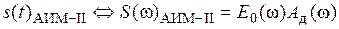где 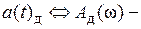спектр отсчетов первичного сигнала .

Спектр одиночного элемента импульсной несущей может быть определен достаточно просто при любой его форме. Так, для прямоугольного импульса с амплитудой U и длительностью 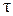имеем

.

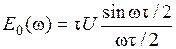Спектр последовательности отсчетов легко получить из спектра сигнала АИМ-I путем предельного перехода при и при амплитуде импульсов 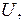стремящейся к бесконечности, так чтобы площадь каждого отсчетного импульса была равна единице. Для прямоугольных импульсов получаем

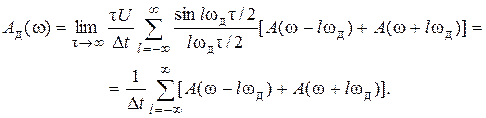
Объединяя и в форме произведения, получаем

.

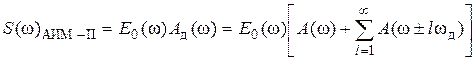Для импульсов в импульсной несущей в форме прямоугольника спектр принимает конкретный вид

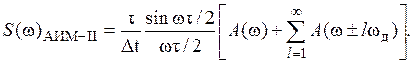(1.4)

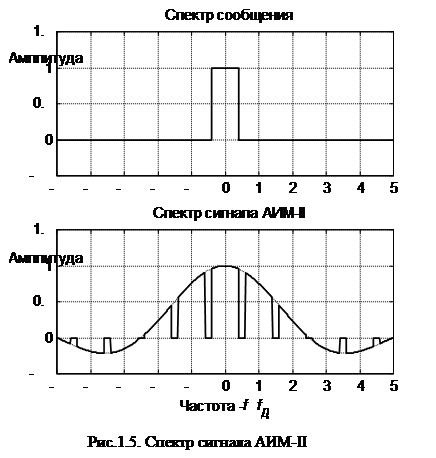
Таким образом, спектр сигнала АИМ-II (рис.1.5) также, как и при АИМ-I, состоит из спектра 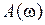модулирующего первичного сигнала и бесчисленного множества боковых полос около каждой гармоники импульсной несущей. Но, в отличие от АИМ-I, здесь перед суммой стоит частотно-зависимый множитель 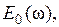равный спектру отдельного элемента импульсной несущей, приводящий к амплитудно-частотным искажениям всех спектральных составляющих, включая и .

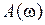Выделение полезной составляющей из спектра сигнала АИМ-II без помех дискретизации здесь также возможно с помощью ФНЧ, при условии, что . Из спектральных диаграмм видно, что степень амплитудно-частотных искажений определяется длительностью 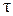отсчетных импульсов в импульсной несущей . При амплитудно-частотные искажения уменьшаются и сигнал АИМ-II практически совпадает с сигналом АИМ-I. С другой стороны, доля полезной составляющей в спектре сигнала как АИМ-I, так и АИМ-II при уменьшается, что, естественно, сказывается на помехозащищенности выделяемого полезного сигнала.

В реальных системах передачи с временным разделением каналов всегда 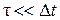. Следовательно, ничтожно малой оказывается доля полезной составляющей. В связи с этим после выделения на приеме отсчетов конкретного сигнала они растягиваются во времени. Возникающие большие амплитудно-частотные искажения затем корректируются с помощью корректора амплитудно-частотных искажений с передаточной функцией

Общей особенностью сигналов АИМ-I и АИМ-II является бесконечно широкая полоса частот, поэтому непосредственное применение таких сигналов в трактах передачи с ограниченной полосой частот нецелесообразно, поскольку из-за ограничения спектра сигнала в тракте форма символов изменяется, что приводит к появлению межсимвольной интерференции в каждом канале и к появлению переходных влияний между каналами. Переходные влияния имеют характер внятных переходных разговоров.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: