 |
Изобразить графически отношения.
|
|
|
|
ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ДИСКРЕТНАЯ МАТЕМАТИКА
КОНТРОЛЬНАЯ РАБОТА
Вариант №1
Выполнил: студент
группы РИС-11-1бзу
Булычева Я.В.
Преподаватель: Файзрахманов Р.А.
Пермь 2013
СОДЕРЖАНИЕ
| Задания | |
| Решения по множествам | |
| Решения по графикам, соответствиям, отношениям | |
| Решения по решеткам | |
| Решения по математической логике | |
| Решения по предикатам | |
| Решения по автоматам |
ЗАДАНИЯ.
ТЕОРИЯ МНОЖЕСТВ [1,4]
№8. Доказать равенство множеств, преобразуя множества к одинаковому виду с помощью основных законов алгебры множеств.
№8.3 (A I B) U (B\A) U (C\B)=B U C.
№9. Доказать равенство множеств, преобразуя множества к одинаковому виду с помощью основных законов алгебры множеств.
№9.12 (А\B)∆B=(А∆В)U(A\ В).
№9.19 (A\B) ∆(B\A) = A∆B.
№10. Решить уравнение относительно X.
№10.10 X I A =A U B.
ГРАФИКИ, СООТВЕТСТВИЯ, ОТНОШЕНИЯ [1,5].
№17 Изобразить графики декартового произведения множеств.
№17.2 В = { y |
3 £ y £8,
y Î R
} и А = { х |
2 £ х £4,
х Î R }.
№17.4 {1, 2, 3}, {2, 3} и {3, 4}.
№17.9 R и N.
№26 Изобразить графически отношения.
№26.4
x =5 (y Î N).
№26.5
x 2 + y 2 = 1 (x, y Î R).
РЕШЕТКИ [1,6]
№32 Доказать.
№32.3 В любой конечной решетке существует наибольший и наименьший элементы.
№33 Привести примеры решеток.
№33.1 Без наибольшего элемента, но с наименьшим элементом.
№34 Являются ли множества, представленные диаграммами
Хассе.
а) решетками;
|
|
|
б) дистрибутивными решетками;
в) булевыми решетками.
|
|
1 2 4
1 1
|
4 5 6
2 3
а б в г д
МАТЕМАТИЧЕСКАЯ ЛОГИКА [2, 7]
№1 Записать в символической форме следующие высказывания:
в) Иванов сдал экзамен и получил пять неравнозначно тому, что
Иванов получил пять и сдал экзамен;
г) если он идёт, то он поезд, но это не значит, что если он стоит, то он поезд;
№7 Построить таблицы истинности для формул:
б) (A(B ®A))® A;
№13 Получить ДНФ для формул:
д) xy Ú xz;
№14 Получить КНФ для формул:
д) x Úy × x Ú y;
№15 Получить СДНФ для формул:
з) `CUZÚC
№16 Получить СКНФ для формул:
а)*
xy Úxz;
№17 Получить СДНФ, а затем перейти к СКНФ:
в) (x Úy Úz)(xÚz)y;
№19 Получить СКНФ, а затем перейти к СДНФ:
д) (x Úy)xyz;
№20 Получить МДНФ для формул:
у) (x Úy Úz)(xÚy Ú z)(xÚy Úz);
ПРЕДИКАТЫ [2, 8]
№25 Записать на языке предикатов:
б) Некоторые студенты отличники;
№29 Записать на языке предикатов:
б) если деталь обеспечена заготовкой, включена в план и для неё есть оснастка, которая может быть использована при обработке данной детали, то эту деталь нельзя оставить на складе или назначить неопытному рабочему.
№35 Придумать содержательные интерпретации формул:
б) $x (P(x) ® R (x));
АВТОМАТЫ [3, 9]
№1 Построить(синхронизировать) автомат по содержательному описанию.
1.9. На вход автомата поступает информация о сдаче трех зачетов. Сначала необходимо сдать зачет 1, затем 2 и 3 в любом порядке. Если все зачеты сданы, то, если заданный порядок был выдержан,
выдается допуск к экзамену, если порядок нарушен, объявляется выговор.
|
4.3 Таблица 18 Таблица 19
| q1 | q2 | q3 | |
| x1 | q2 | q1 | q3 |
| x2 | q3 | q2 | q2 |
| x3 | q2 | q3 | q1 |
№5 Преобразовать автомат Мура в автомат Мили:
5.3 Таблица 26
| y1 | y2 | y1 | y2 | y3 | |
| q0 | q1 | q2 | q3 | q4 | |
| x | q1 | q2 | q3 | q4 | q0 |
№7 Минимизировать автомат Мили:
|
| x1 | ||||||||
| x2 | ||||||||
| x3 |
РЕШЕНИЯ.
ТЕОРИЯ МНОЖЕСТВ [1,4]
№8. Доказать равенство множеств, преобразуя множества к одинаковому виду с помощью основных законов алгебры множеств.
№8.3 (A I B) U (B\A) U (C\B)=B U C. Решение:
(A I B) U (B \ A) U (C \ B) = [(A I B) U (B I A)]U (C I B)=
= [((A I B) U B) I ((A I B) U A)]U (C I B) = [ B I ((B U A)I (A U A))]U (C I B) =
= [ B I (B U A)]U (C I B)= [ B ]U (C I B)= (B U C)I (B U B)= (B U C)I U = B U C
Что и требовалось доказать.
№9. Доказать равенство множеств, преобразуя множества к одинаковому виду с помощью основных законов алгебры множеств.
№9.12 (А\B)∆B=(А∆В)U(A\ В). Решение:
(A \ B)D B =((A \ B)\ B)U(B \ (A \ B))=((A I B)\ B)U(B \ (A I B))=
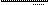
= ((A I B)I B)U (B I (A I B))= (A I B)U (B I (A U B)=
=(A I B)U(B I(A U B))
(A D B)U(A \ B)=((A \ B)U(B \ A))U(A I B)=
= ((A I B)U (B I A))U (A I B) = (A I B)U ((B I A)U (A I B)) =
= (A I B)U ((B I A) U (B I B) U (A I A)U (A I B))=
= (A I B)U ((B U A)I B)= (A I B)U (B I (B U A))
Получаем, что слева и справа множества приводятся к одному виду:
(A I B)U (B I (A U B)) = (A I B)U (B I (B U A))
№9.19 (A\B) ∆(B\A) = A∆B. Решение:
(A \ B)D(B \ A) = [(A \ B) \ (B \ A)]U [(B \ A) \ (A \ B)] =
=[(A \ B)I(B \ A)]U[(B \ A)I(A \ B)]=[(A \ B)]U[(B \ A)]=(A \ B)U(B \ A)
A D B = (A \ B) U (B \ A)
Получаем, что слева и справа множества приводятся к одному виду:
№10. Решить уравнение относительно X.
№10.10 X IA =A UB.
Решение:
1. Представим уравнение в виде:
F 1 (X)D F 2 (X)=Æ
2. Используя законы алгебры множеств, преобразуем уравнение к виду: (C I X) U (D I X) = Æ
где C и D – некоторые множества не содержащие множество X или его дополнение.
(X I A)D(A U B)=Æ
[(X I A)\ (A U B)]U[(A U B)\ (X I A)]=Æ
[(X I A)I(A U B)]U[(A U B)I(X I A)]=Æ
[(X I A)I (A U B)]U [(A I B)I (X U A)]= Æ
[ X I (A I (A U B))]U [(X U A)I (A I B)] = Æ
|
|
|
[ X I A ]U [((X U A)I A)I B ] = Æ
(X I A) U (A I B)= Æ
Получили выражение, которое не сводится прямо к виду
(C I X)U(D I X)=Æ
Мешает выражение (A I B). Поэтому, воспользовавшись законом исключённого третьего (A U A = U), пересечём скобку (A I B) с универсумом (X U X) (что не нарушает равенства):
(X I A) U [(A I B)I (X U X)] = Æ
Преобразуем, применяя дистрибутивный закон:
(X I A)U[(A I B I X)U(A I B I X)]=Æ
(X I A) U (A I B I X)U (A I B I X)= Æ
(X I (A U (A I B)))U ((A I B)I X)= Æ
3. Для искомого множества выполняется соотношение
(A I B) Í X Í (A U (A I B)) или
(A I B) Í X Í A I (A U B) или
D Í X Í C, т.е.
A I B Í X Í A I B
ГРАФИКИ, СООТВЕТСТВИЯ, ОТНОШЕНИЯ [1,5].
№17 Изобразить графики декартового произведения множеств.
№17.2 В = { y |
3 £ y £8,
y Î R
} и А = { х |
2 £ х £4,
х Î R }.
Решение: A ´ B ={< x, y >2 £ x £4,3 £ y £8; x, y Î R }
y
8
x
2 4
Элемент
z =< x, y >Î A ´ B
изображается точкой на плоскости внутри
прямоугольника.
№17.4 {1, 2, 3}, {2, 3} и {3, 4}.
Решение: обозначим
A ={1,2,3}, B ={2,3}, C ={3,4},
Z(C)
Y(B)
3
1 2 3
X(A)
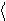
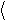
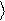
A ´ B ´ C ={1,2,3, 1,2,4, 1,3,3, 1,3,4,
2,2,3,
2,2,4,
2,3,3,
2,3,4,
3,2,3,
3,2,4,
3,3,3,
3,3,4 }
Расположив множества A, B, C, на осях x, y, z, соответственно, получим графическую интерпретацию декартова произведения множеств.
№17.9 R и N.
Решение:
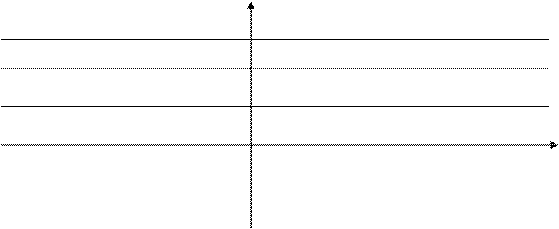
R ´ N ={(x, y): x Î R, y Î N }
Y
.... 4....
.... 3....
.... 2....
. -5. -4. -3.-2 1.2.3.4.5
X
.... -2....
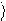Элемент z =
линиях.
x, y
Î R ´ N
изображается точками на параллельных
Изобразить графически отношения.
№26.4
x =5 (y Î N).
Решение:
На графике это будет множество точек с натуральными ординатами, лежащих на прямой х=5
y
9.
8.
7.
6.
5.
4.
3.
2.
1.
x
5
№26.5
x 2 + y 2 =1 (x, y Î R).
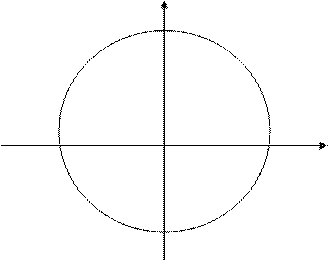Решение: Y
-1 1 X
-1
РЕШЕТКИ [1,6]
№32 Доказать.
№32.3 В любой конечной решетке существует наибольший и наименьший элементы.
Доказательство:
|
|
|
1. Конечная решётка ограничена, т.к. для любого конечного набора
элементов решётки А можно найти
a Ï A: x < a " x Î A, b Ï A: x > b " x Î A
2. Таким образом, решётка А имеет максимальный и минимальный элементы, совпадающие с точной верхней и точной нижней гранями.
№33 Привести примеры решеток.
№33.1 Без наибольшего элемента, но с наименьшим элементом. Решение:
1. Такой решёткой может быть множество натуральных чисел N:
наибольшего элемента нет, т.к.
y = x +1
" x Î N $ y Î N: x < y, например, если
2. Множество
R +={ x Î R, x ³0}.
№34 Являются ли множества, представленные диаграммами
Хассе.
а) решетками;
б) дистрибутивными решетками;
в) булевыми решетками.
|
|
1 2 4
1 1
|
4 5 6
2 3
а б в г д
Решение:
а) решётками данные множества являются, т.к. они частично упорядочены и для их элементов справедливы следующие законы:
1. Коммутативный
2. Ассоциативный
a I b = b I a, a U b = b U a
a I (b I c) = (a I b) I c, a U (b U c) = (a U b) U c
3. Идемпотентности
a I a = a, a U a = a
4. Поглощения
a I (a U b) = a, a U (a I b) = a
б) Решётка называется дистрибутивной, если справедлив, кроме того,
дистрибутивный закон:
a I (b U c) = (a I b) U (a I c), a U (b I c) = (a U b) I (a U c)
Решётка на рисунке (г) не дистрибутивная, т.к. например, для элементов 2,3,4 дистрибутивный закон не выполняется.
в) Решётка называется решёткой с дополнениями, если каждый элемент решётки имеет хотя бы одно дополнение. Ограниченная дистрибутивная решётка с дополнениями называется булевойрешёткой, которая фактически задаёт булеву алгебру.
Дополнением любого элемента
a Î A
называется такой элемент a,
если
a U a =1,
a I a =0, где 1 и 0-соответственно обозначения
максимального и минимального элементов ограниченной решётки. На рисунке (б) приведена решётка, у элементов которой есть дополнения
и для любого элемента
a Î A
называется такой элемент a, если
a U a =1,
a I a =0, где 1 и 0-соответственно обозначения
максимального и минимального элементов ограниченной решётки. Из приведённых, булевой решёткой является решётка на рисунке (б).
МАТЕМАТИЧЕСКАЯ ЛОГИКА [2, 7]
№1 Записать в символической форме следующие высказывания:
в) Иванов сдал экзамен и получил пять неравнозначно тому, что
Иванов получил пять и сдал экзамен;
Решение: Выберем элементарные высказывания следующим образом:
А- Иванов сдал экзамен
В- Иванов получил пять;
Тогда символическая форма сложного высказывания будет иметь вид
(А ® И) Å (В ® А)
|
|
|
г) если он идёт, то он поезд, но это не значит, что если он стоит, то он поезд;
Решение: Выберем элементарные высказывания следующим образом:
А- Он идёт
В- Он поезд
С- Он стоит
Тогда символическая форма сложного высказывания будет иметь вид
(А ® В) Å (С ® В)
№7 Построить таблицы истинности для формул:
б) (A(B ®A))® A;
Решение:
| А | В | Ø A | В ® А | А & (B ® A) | (A & (B ® A))®Ø A |
| I | |||||
| I | I | ||||
| I | I | ||||
| I | I | I | I |
№13 Получить ДНФ для формул:
д) xy Ú xz;
Решение:
Элементарной конъюнкцией называется выражение вида
В 1 × В 2 ×....× Вn
где каждое
Bi (i = 1, n)
является либо элементарным
высказыванием, либо отрицанием элементарного высказывания. Дизъюнктивной нормальной формой (ДНФ) данного высказывания называется равносильное ему высказывание вида
K 1 Ú K 2
Ú... Ú K s
, K i
(i =1, s)-элементарная конъюнкция.
Преобразуем выражение:
xy Ú xz º x Ú y Ú x Ú z º xx Ú yy Ú zz
№14 Получить КНФ для формул:
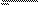д) x Úy × x Ú y;
Решение:
Элементарной дизъюнкцией называется выражение вида
A 1 Ú A 2 Ú...Ú An
где каждое
Ai (i = 1, n)
является либо элементарным
высказыванием, либо отрицанием элементарного высказывания. Конъюнктивной нормальной формой (КНФ) данного высказывания
называется равносильное ему высказывание вида
|
D 1 × D 2 ×...× Dt, где
Преобразуем выражение: (x & y)× x & y º x & y & x & y
Можно также упростить выражение, воспользовавшись коммутативным законом:
º x & y & x º y & 0 º 0
№15 Получить СДНФ для формул:
з) `CUZÚC
Решение:
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая ДНФ, в которой каждая элементарная конъюнкция (называемая
также конституантой единицы) содержит все элементарные высказывания либо их отрицания по одному разу. Конституанты единицы в СДНФ не повторяются.
Преобразуем выражение:
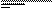
xyz Ú x º xyz & x º xyz
№16 Получить СКНФ для формул:
а) *
xy Úxz;
Решение:
Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, в которой каждая элементарная дизъюнкция (называемая также конституантой нуля) содержит все элементарные высказывания либо их отрицания по одному разу. Конституанты нуля в СКНФ не повторяются.
Преобразуем выражение:
xy Ú xz º (xy Ú x)(xy Ú z) º (x Ú x)(x Ú y)(x Ú z)(y Ú z) º
º (x Ú y Ú zz)(x Ú z Ú yy)(y Ú z Ú xx) º
º(x Ú y Ú z)(x Ú y Ú z)(x Ú y Ú z)(x Ú y Ú z)
№17 Получить СДНФ, а затем перейти к СКНФ:
в) (x Úy Úz)(xÚz)y;
Решение:
(x Ú y Ú z)(x Ú z) y º (x Ú y Ú z)(xy Ú zy)º (xxy Ú yxy Ú zxy Ú x zy Ú y zy Ú z zy) º
º(xy Ú zxy Ú x zy)º(xy (z Ú z)Ú zxy Ú x zy)º(xyz Ú xy z Ú zxy Ú x zy)º(xyz Ú xyz)
Получили СДНФ, теперь перейдём к СКНФ. При переходе СДНФ к СКНФ в начале необходимо получить отрицание исходного высказывания за счёт выписывания через дизъюнкцию недостающих (до полного перечня) конституант единицы, а затем взять отрицание
этого высказывания и выполнить преобразования по закону Де Морга:
f = (xyz Ú x yz)
f = xyz Ú xyz Ú xyz Ú xyz Ú xyz Ú xyz
f = xyz Ú xyz Ú xyz Ú xyz Ú xyz Ú xyz º
º(x Ú y Ú z)(x Ú y Ú z)(x Ú y Ú z)(x Ú y Ú z)(x Ú y Ú z)(x Ú y Ú z)
№19 Получить СКНФ, а затем перейти к СДНФ:
д) (x Úy)xyz;
Решение:
Преобразуем выражение: (x Ú y) xyz º(xxyz)Ú(yxyz)º(xyz)Ú(xyz)º xyz
Получили сразу СДНФ. Теперь перейдём к СКНФ аналогично примеру
№17.
f = xyz
f = xyz Ú xyz Ú xyz Ú xyz Ú xyz Ú xyz Ú x yz
f = xyz Ú xyz Ú xyz Ú xyz Ú xyz Ú xyz Ú x yz º
º(x &Uacut
|
|
|
