 |
Построить скользящие средние для ценового графика (выбрать самостоятельно). Расчеты оформляются в табличной форме и строятся графики скользящих средних. Сделать выводы о вхождении на рынок.
|
|
|
|
Простая Скользящая средняя (SMA)
Простая Скользящая средняя формируется путем вычисления средней цены рыночного инструмента за указанное число периодов. Хотя возможно формировать Скользящие средние исходя из цены открытия, максимума и минимума, большинство Скользящих средних использует цену закрытия.
Простое скользящее среднее определяется по формуле:
, (1)
где SMAt — значение простого скользящего среднего в точке t; n — количество значений исходной функции для расчёта скользящего среднего; pt-i — значение исходной функции в точке t-i.
Последующее значение скользящего среднего рассчитывается на основе предыдущего:
(2)
где SMAt-1 — предыдущее значение простого скользящего среднего, p t-n — значение исходной функции в точке t=n; pt — значение исследуемой функции точке t (в случае временного ряда последнее значение).
Например: значение 5-дневной Простой Скользящей средней рассчитано суммированием цен закрытия в течение прошлых 5 дней и делением общей суммы на 5. Например:
10+11+12+13+14=60;
60/5=12.
Вычисление повторяется для каждого ценового бара (свечи) на графике. Затем средние значения соединяются и формируют гладкую изгибающуюся среднюю линию. Продолжим пример: если следующая цена закрытия равна 15, то этот новый период будет добавлен, а самый первый день, для которого значение равно 10, будет исключен. Новое значение 5-дневной Простой Скользящей средней будет рассчитано следующим образом:
11+12+13+14+15=65;
65/5=13.
За последние два дня, SMA продвинулась от 12 до 13. Поскольку новые дни добавляются, прошлые дни будут выбывать, и Скользящая средняя будет продолжать двигаться дальше.
Рис. 4 – Простая скользящая средняя
Взвешенная скользящая средняя (WMA).
|
|
|
При построении скользящей средней некоторые значение исходной функции целесообразно сделать более значимым. Например, последние значения цен более актуальные и могут быть весомее предыдущих.
Взвешенное скользящее среднее, как и экспоненциальное, придает более поздним данным больше “веса”, но оно делает это более выражено и проще. При просчете 5-ти дневного взвешенного скользящего среднего, мы придаем текущей цене пятикратный вес, вчерашней — четырехкратный, позавчерашней — трехкратный и т.д., а потом делим сумму всех произведений на сумму добавленного веса:
(1·8+2·8+3·9+4·10+5·11)/(1+2+3+4+5) = 146/15 = 9,73.
Какую Скользящую среднюю использовать, зависит от стиля торговли и предпочтений. Простая Скользящая средняя, очевидно, имеет запаздывание. Экспоненциальная Скользящая средняя может быть склонна к более быстрым прорывам. Некоторые трейдеры предпочитают использовать Экспоненциальные Скользящие средние для более коротких периодов времени для более быстрого отображения изменений. Некоторые инвесторы предпочитают для долгосрочных периодов Простые Скользящие средние, чтобы определять долгосрочные изменения трендов. Кроме того, многое будет зависеть от конкретного рыночного инструмента.
Рис. 5 – Взвешенная скользящая средняя
Экспоненциальная Скользящая средняя (EMA)
Чтобы снизить запаздывание в Простых Скользящих средних, трейдеры часто используют Экспоненциальные Скользящие средние (также называемые «Скользящие средние взвешенные по экспоненте»). EMA уменьшает запаздывание, придавая больший вес недавним ценам относительно более ранних цен.
Экспоненциально взвешенное скользящее среднее рассчитывается следующим образом:
(3)
где EMAt — значение экспоненциального скользящего среднего в точке t (последнее значение, в случае временного ряда), EMAt-1 — значение экспоненциального скользящего среднего в точке t -1 (предыдущее значение в случае временного ряда), pt — значение исходной функции в момент времени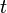 
(последнее значение в случае временного ряда), α (сглаживающая константа) — коэффициент характеризующий скорость уменьшения весов, принимает значение от 0 и до 1, чем меньше его значение тем больше влияние предыдущих значений на текущую величину среднего.
|
|
|
Первое значение экспоненциального скользящего среднего обычно принимается равным первому значению исходной функции:
(4)
Коэффициент α равен:
(5)
где n - указанное число периодов.
Рис. 6 – Экспоненциальная скользящая средняя
Задание 4.
|
|
|
