 |
Тема 5. Теорема косинусов и уравнения
|
|
|
|
Пусть даны n чисел 
причем 
>0, 
и n-1 положительных чисел 
такие, что 
. На координатной плоскости ось абсцисс обозначим через 
. Повернем вокруг начала координат против часовой стрелки на угол 
, где i=1,2,…,n-1, полученную прямую обозначим через 
. На каждой прямой 
отложим числа 
, обозначив соответствующую точку 
(см. рис1). По теореме косинусов (если одно из чисел , 
отрицательно, то угол 
равен 
) при любом i=1,2,…,n-1 имеем:
(заметим, что первое равенство справедливо и в случае, если одно из чисел , равно нулю). Так как длина ломанной 
не меньше длины отрезка 
, то справедливо неравенство
, (1)
при этом равенство имеет место тогда и только тогда, когда точки (i=2,3,…,n-1) лежат на отрезке .
Рис.1
Пусть теперь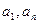 
являются фиксированными числами, а 
- функциями от n-2 переменных 
. Тогда уравнение
(2)является уравнением с n-2 неизвестными (переменными) и получено обращение неравенства (1).Поэтому набор () будет решением уравнения (2) в том случае, если точки , соответствующие значению функции на этом наборе, лежат на отрезке .
Приведем примеры уравнений вида (2).
Пример 1. Решите уравнение
Решение. Алгебраический метод. ОДЗ уравнения – множество всех действительных чисел. Перепишем уравнение как
и возведем обе части его в квадрат. После приведения подобных получим уравнение
Еще раз возведем обе части уравнения в квадрат. Тогда
отсюда получаем, что 
. Теперь мы должны проверить, что 
является решением исходного уравнения.
Геометрический метод. Коэффициент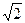 
при х позволяет сделать предположение, что уравнение имеет вид (2). Примем
Тогда
и, значит, уравнение имеет вид (2). Построим аналог рисунка для этого случая (см. рис. 2). Так как неравенство (1) обращается в равенство, если только
|
|
|
рис. 2
точка 
лежит на отрезке 
, то решение уравнения сводится к вычислению длины биссектрисы треугольника 
, проведенной из вершины О. Как известно, длина биссектрисы треугольника, проведенной из угла, равного 
, может быть вычислена по формуле (выводимой опять с помощью теоремы косинусов)
Поэтому 
и, значит, заданное уравнение имеет единственное решение .
Преимущество геометрического метода в его наглядности. Отпадает необходимость в проверке, которая требует рутинных вычислений. Есть возможность при решении уравнений использовать геометрические факты.
Пример 2. Решите уравнение
Решение. Алгебраический метод таков же, как и при решении предыдущего примера. Отличие состоит только в большем числе преобразований и усложнении проверки (возникновение постороннего решения).
Геометрический метод. Коэффициент 
при х показывает, что возможно уравнение имеет вид (2). Положим
Тогда
.
Поэтому данное уравнение имеет вид (2). Построим аналог рисунка для этого случая (см. рис. 3). Ясно, что число х будет решением уравнения в том и только в том случае, если точка лежит на отрезке . Поскольку 
и
+ 
,
(*)
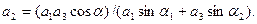Отсюда находим, что 
и, значит, 
.
Рис. 3
Как видим, геометрический метод сопровождается геометрическими рассуждениями, обоснованием своих выводов, сделанных на основе чертежа. Это положительно сказывается на развитии мышления учащихся и предупреждает формализм, присущий алгебраическому методу решения подобных иррациональных уравнений.
Пример 3. Докажите, что уравнение
равносильно системе уравнений
Найдите их решение.
Решение. Алгебраический метод при решении подобных задач (как было показано при решении задач примеров 1 и 2) малоэффективен.
Геометрический метод. Примем
Нетрудно заметить, что: заданное уравнение – это уравнение вида (2) для данного случая; первое уравнение системы – Это уравнение (2) для случая 
второе уравнение системы – для случая 
Построив аналог рисунка (рис. 4), замечаем, что пара (х;у) будет
|
|
|
Рис. 4
решением уравнения тогда и только тогда, когда она будет решением системы. Следовательно, уравнение и система равносильны. Подставляя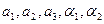 
для уравнений системы в формулу (*), находим (см. решение предыдущего примера), что 
.
Как и при решении предыдущего уравнения использовались геометрические рассуждения. При обосновании выводов использовался чертеж.
|
|
|
