 |
Динамический анализ и синтез механизьмов.
|
|
|
|
1.Силовой расчет механизьмов. Задачи силового расчета. Условие статической определимости. Порядок силового расчета.
Задачи силового расчета: Определение всех сил и моментов (по осям) приложенных к каждому отдельному звену механизма. Механизм находится в равновесии при условии, что к одному из его звеньев приложена уравновешивающая сила или уравновешивающий момент, который обычно прикладывается к ведущему звену. Порядок силового расчета 1.Определяются все внешние нагрузки, действующие на звенья механизма. 2.Выделяются гр.Ассура 3.Производится силовой расчет с наиболее удаленной группой. 4.Последним рассчитывается ведущее начальное звено, использую уравнения равновесия 
2.Силовой расчет группы Ассура второго класса с поступательной парой. Определение реакции в поступательной паре.
Определение реакций в кинематических парах группы Ассура II класса 1-го вида (ВВВ).  Рис. 6.3. Силовой расчет группы типа ВВВ: а – схема группы; б – план ускорений; в – план сил группы. Пусть даны силы тяжести G2 и G3 звеньев 2 и 3; сила полезного сопротивления Рпс; моменты инерции
Рис. 6.3. Силовой расчет группы типа ВВВ: а – схема группы; б – план ускорений; в – план сил группы. Пусть даны силы тяжести G2 и G3 звеньев 2 и 3; сила полезного сопротивления Рпс; моменты инерции  относительно осей, проходящих через центры масс звеньев 2 и 3. Определим реакции в кинематических парах А, В, О3. Вычисляем силы инерции (главные векторы Ри и главные моменты сил инерции Ми) по формулам
относительно осей, проходящих через центры масс звеньев 2 и 3. Определим реакции в кинематических парах А, В, О3. Вычисляем силы инерции (главные векторы Ри и главные моменты сил инерции Ми) по формулам  (6.15) где
(6.15) где  – линейные ускорения центров масс звеньев 2 и 3, принимаем с планов ускорений (рис. 6.3, б);
– линейные ускорения центров масс звеньев 2 и 3, принимаем с планов ускорений (рис. 6.3, б);  – угловые ускорения звеньев 2 и 3. Вычисленные силы инерции
– угловые ускорения звеньев 2 и 3. Вычисленные силы инерции  прикладываем в точках S2 и S3 (рис.6.3, а) противоположно векторам
прикладываем в точках S2 и S3 (рис.6.3, а) противоположно векторам  (рис.6.3, б). Моменты от пар сил инерции М2 и М3направляем противоположно угловым ускорениям
(рис.6.3, б). Моменты от пар сил инерции М2 и М3направляем противоположно угловым ускорениям  . Реакции во внешних парах А и О3 разложим на две составляющие, направленные по осям звеньев 2 и 3 и перпендикулярно к этим осям, и обозначим их соответственно через
. Реакции во внешних парах А и О3 разложим на две составляющие, направленные по осям звеньев 2 и 3 и перпендикулярно к этим осям, и обозначим их соответственно через  . Тангенциальные составляющие находим из уравнений моментов всех сил относительно точки В для каждого звена в отдельности. Для звена 2 имеем:
. Тангенциальные составляющие находим из уравнений моментов всех сил относительно точки В для каждого звена в отдельности. Для звена 2 имеем:  (6.16) Из этого уравнения находим
(6.16) Из этого уравнения находим  . Аналогично составляем уравнение моментов для звена 3:
. Аналогично составляем уравнение моментов для звена 3:  (6.17) Отсюда находим
(6.17) Отсюда находим  . Все плечи в уравнения моментов подставляем в миллиметрах, взяв их непосредственно с чертежа. Нормальные составляющие
. Все плечи в уравнения моментов подставляем в миллиметрах, взяв их непосредственно с чертежа. Нормальные составляющие  определяем, решая графически векторное уравнение равновесия структурной группы (звенья 2,3),
определяем, решая графически векторное уравнение равновесия структурной группы (звенья 2,3),  (6.18) В этом уравнении все силы, кроме
(6.18) В этом уравнении все силы, кроме  , известны и по величине и по направлению. Реакции
, известны и по величине и по направлению. Реакции  известны только по направлению. Уравнение (6.18) решаем графически, строя план сил в некотором масштабе
известны только по направлению. Уравнение (6.18) решаем графически, строя план сил в некотором масштабе  (рис.6.3, в). Для этого последовательно откладываем все известные силы, перенося их из плана группы на план сил параллельно самим себе. Затем из начала вектора
(рис.6.3, в). Для этого последовательно откладываем все известные силы, перенося их из плана группы на план сил параллельно самим себе. Затем из начала вектора  и конца вектора
и конца вектора  проводим прямые, параллельные соответственно звеньям 2 и 3. Точка пересечения этих прямых определит длины векторов
проводим прямые, параллельные соответственно звеньям 2 и 3. Точка пересечения этих прямых определит длины векторов  . Для определения реакций в шарнире В решаем графически векторное уравнение сил, приложенных к одному из звеньев, например, к звену 2. Отбрасываем звено 3 и его действие заменяем реакцией
. Для определения реакций в шарнире В решаем графически векторное уравнение сил, приложенных к одному из звеньев, например, к звену 2. Отбрасываем звено 3 и его действие заменяем реакцией  , которую определяем из графического решения уравнения.
, которую определяем из графического решения уравнения.  (6.19) Определение реакций в кинематических парах групп Ассура II класса 4-го вида. Данный механизм состоит из двух групп Ассура II класса 4-го вида (звенья 4–5) и 3-го вида (звенья 2–3). Рассмотрим особенности силового расчета группы Ассура, состоящей из звеньев (4–5) (рис.6.4, г). Это группа образована двумя ползунами, соединенными между собой поступательной кинематической парой. На данную структурную группу действуют следующие силы: тяжести звена 5G5, полезного сопротивления РПС и инерции звена 5Р5. Масса звена 4 мала по сравнению с массами остальных звеньев и ею можно пренебречь. Значит, G4 = 0 и Р4 = 0. Исполнительное звено (ползун 5) образуют со стойкой поступательную пару в точке Е’ и дублирующую в точке Е”.Реакции этих пар приводятся к равнодействующей R05, приложенной в точке Е”. В точке С свободной (внешней) парой является вращательная, соединяющая ползун 4 с кулисой 3. В общем случае реакция R34 этой пары не известна по величине и направлению. Направление реакции R34 установим, рассмотрев равновесие звена 4 (рис.6.4, е). Так как это звено невесомое, то оно будет находиться в равновесии под действием двух сил – R34 и R54. Значит, эти силы равны и противоположно направлены. R54 – это сила действия направляющей звена 5 на звено 4. Известно, что без учета сил трения направление реакции R54 перпендикулярно к направляющим ползуна 4, следовательно и реакция R34 во вращательной кинематической паре будет иметь такое же направление. Уравнение равновесия структурной группы 4–5 имеет вид
(6.19) Определение реакций в кинематических парах групп Ассура II класса 4-го вида. Данный механизм состоит из двух групп Ассура II класса 4-го вида (звенья 4–5) и 3-го вида (звенья 2–3). Рассмотрим особенности силового расчета группы Ассура, состоящей из звеньев (4–5) (рис.6.4, г). Это группа образована двумя ползунами, соединенными между собой поступательной кинематической парой. На данную структурную группу действуют следующие силы: тяжести звена 5G5, полезного сопротивления РПС и инерции звена 5Р5. Масса звена 4 мала по сравнению с массами остальных звеньев и ею можно пренебречь. Значит, G4 = 0 и Р4 = 0. Исполнительное звено (ползун 5) образуют со стойкой поступательную пару в точке Е’ и дублирующую в точке Е”.Реакции этих пар приводятся к равнодействующей R05, приложенной в точке Е”. В точке С свободной (внешней) парой является вращательная, соединяющая ползун 4 с кулисой 3. В общем случае реакция R34 этой пары не известна по величине и направлению. Направление реакции R34 установим, рассмотрев равновесие звена 4 (рис.6.4, е). Так как это звено невесомое, то оно будет находиться в равновесии под действием двух сил – R34 и R54. Значит, эти силы равны и противоположно направлены. R54 – это сила действия направляющей звена 5 на звено 4. Известно, что без учета сил трения направление реакции R54 перпендикулярно к направляющим ползуна 4, следовательно и реакция R34 во вращательной кинематической паре будет иметь такое же направление. Уравнение равновесия структурной группы 4–5 имеет вид  (6.20) В данном векторном уравнении неизвестными являются только две силы R05 и R34, поэтому его решение выполним графически методом построения плана сил (рис.6.4, д).
(6.20) В данном векторном уравнении неизвестными являются только две силы R05 и R34, поэтому его решение выполним графически методом построения плана сил (рис.6.4, д).
|
|
|
|
|
|
 Рис. 6.4. Силовой расчет кривошипно-кулисного механизма: а – кинематическая схема механизма; б – план скоростей; в – план ускорений; г – расчетная схема группы 4–5; д – план сил группы 4–5; е – расчетная схема ползуна 4; ж – расчетная схема группы 2–3; з – план сил группы 2–3. Определение реакций в кинематических парах групп Ассура II класса 3-го вида (рис.6.4, ж). Эта группа находится в равновесии под действием внешних сил: R43 = –R34, величина и направление которой определены из предыдущих расчетов; силы тяжести G3 звена 3; силы инерции и момента сил инерции звена 3, определение которых выполняются по зависимостям (6.21). Масса звена 2 мала по сравнению с массами остальных звеньев и ею можно пренебречь. Значит, G2 = 0, Р2 = 0. Реакции, подлежащие определению: R12, приложенная в центре шарнира А, и R03, приложенная в центре шарнира О3. Вычисляем силы инерции, действующие на звено 3,
Рис. 6.4. Силовой расчет кривошипно-кулисного механизма: а – кинематическая схема механизма; б – план скоростей; в – план ускорений; г – расчетная схема группы 4–5; д – план сил группы 4–5; е – расчетная схема ползуна 4; ж – расчетная схема группы 2–3; з – план сил группы 2–3. Определение реакций в кинематических парах групп Ассура II класса 3-го вида (рис.6.4, ж). Эта группа находится в равновесии под действием внешних сил: R43 = –R34, величина и направление которой определены из предыдущих расчетов; силы тяжести G3 звена 3; силы инерции и момента сил инерции звена 3, определение которых выполняются по зависимостям (6.21). Масса звена 2 мала по сравнению с массами остальных звеньев и ею можно пренебречь. Значит, G2 = 0, Р2 = 0. Реакции, подлежащие определению: R12, приложенная в центре шарнира А, и R03, приложенная в центре шарнира О3. Вычисляем силы инерции, действующие на звено 3,  (6.21) где
(6.21) где  – ускорение центра масс звена 3, берем с плана ускорений (рис.6.5, б),
– ускорение центра масс звена 3, берем с плана ускорений (рис.6.5, б),  (м/с2);
(м/с2);  – угловое ускорение звена 3. Прикладываем вектор силы Р3 в точку S3 (рис.6.4,ж) противоположно вектору πS3, а момент М3 – к звену 3 противоположно вектору e3. Составим уравнение равновесия всех сил, действующих на звенья 2,3,
– угловое ускорение звена 3. Прикладываем вектор силы Р3 в точку S3 (рис.6.4,ж) противоположно вектору πS3, а момент М3 – к звену 3 противоположно вектору e3. Составим уравнение равновесия всех сил, действующих на звенья 2,3,  . (6.22) Это векторное уравнение можно решить графически, если предварительно найти модуль силы R12. Направление реакции R12 находим, рассмотрев равновесие звена 2 (рис.6.4). Так как это звено невесомое, то оно будет находиться в равновесии под действием двух сил – R12 и R32. Значит, эти силы равны и противоположно направлены. R32 – это сила действия направляющей ВО3 на звено 2. Известно, что без учета сил трения реакция R32 направлена перпендикулярно к направлению ВО3. Зная направление R12, найдем её модуль из уравнения моментов всех сил относительно точки О3
. (6.22) Это векторное уравнение можно решить графически, если предварительно найти модуль силы R12. Направление реакции R12 находим, рассмотрев равновесие звена 2 (рис.6.4). Так как это звено невесомое, то оно будет находиться в равновесии под действием двух сил – R12 и R32. Значит, эти силы равны и противоположно направлены. R32 – это сила действия направляющей ВО3 на звено 2. Известно, что без учета сил трения реакция R32 направлена перпендикулярно к направлению ВО3. Зная направление R12, найдем её модуль из уравнения моментов всех сил относительно точки О3  , (6.23) откуда находим R12. Уравнение (6.22) решаем графически методом построения плана сил. Реакция R03 замыкает силовой многоугольник, построенный по уравнению (6.22).
, (6.23) откуда находим R12. Уравнение (6.22) решаем графически методом построения плана сил. Реакция R03 замыкает силовой многоугольник, построенный по уравнению (6.22).
3.Силовой расчет ведущего звена. Определение уравновешивающей силы и реакции в стойке.

 В задачу силового расчета ведущего звена входит определение уравновешивающей силы и реакции в шарнире О1 для заданного положения. Вычерчиваем ведущее звено в ранее выбранном масштабе
В задачу силового расчета ведущего звена входит определение уравновешивающей силы и реакции в шарнире О1 для заданного положения. Вычерчиваем ведущее звено в ранее выбранном масштабе  в заданном положении и прикладываем к нему силу тяжести звена - G1, силу инерции - Fин1, уравновешивающую силу - Fур, силу реакции R21, с которой звено 2 действует на звено 1. Сила реакции R21 равна по величине и противоположна по направлению силе R12. Уравновешивающая сила Fур, величину которой надо определить, приложена к шарниру А и направлена перпендикулярно к оси кривошипа. Предположим, что Fур направлена в сторону вращения кривошипа. В шарнире О1 действует реакция со стороны стойки R41, величина и направление которой неизвестны. Величину уравновешивающей силы определим из уравнения равновесия звена 1
в заданном положении и прикладываем к нему силу тяжести звена - G1, силу инерции - Fин1, уравновешивающую силу - Fур, силу реакции R21, с которой звено 2 действует на звено 1. Сила реакции R21 равна по величине и противоположна по направлению силе R12. Уравновешивающая сила Fур, величину которой надо определить, приложена к шарниру А и направлена перпендикулярно к оси кривошипа. Предположим, что Fур направлена в сторону вращения кривошипа. В шарнире О1 действует реакция со стороны стойки R41, величина и направление которой неизвестны. Величину уравновешивающей силы определим из уравнения равновесия звена 1 
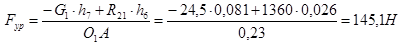 Длины h6 и h7 берем на чертеже. Уравнение решаем и определяем числовое значение Fур. Неизвестную по величине и направлению реакцию R41 определить из векторного уравнения равновесия звена 1:
Длины h6 и h7 берем на чертеже. Уравнение решаем и определяем числовое значение Fур. Неизвестную по величине и направлению реакцию R41 определить из векторного уравнения равновесия звена 1: 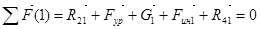
|
|
|
Уравнение решаем графически, строя замкнутый силовой многоугольник. Для определения численного значения R41 измеряем на чертеже длину соответствующего вектора и умножаем на масштаб  .
.
R41 = 151,6 ∙ 10 = 1516 H.
4.Определение уравновешивающей силы с помощью рычага Жуковского. Пример.
Для нахождения уравновешивающей силы необходимо: 1.построить повернутый на 900 в любую сторону план скоростей2.Найти на этом плане по правилу подобия точки приложения заданных внешних сил.3.В одноименные точки плана перенести параллельно самим себе все внешние силы, включая и Рур. Моменты заменить на пары сил.4.Принять повернутый план скоростей за рычаг с точкой опоры в полюсе Р и найти уравновешивающую силу из уравнения равновесия этого рычага.
5.Задачи динамики. Классификация сил и работ, возникающих при движении машины. Режимы работы движения машины. Цикл движения.
Динамика - раздел механики машин и механизмов, изучающий закономерности движения звеньев механизма под действием приложенных к ним сил. Есть такое определение: "Динамика рассматривает силы в качестве причины движения тел". В основе динамики лежат три закона, сформулированные Ньютоном, из которых следует: Из первого закона: Если равнодействующая всех внешних сил, действующих на механическую систему равно нулю, то система находится в состоянии покоя.
Из второго закона: Изменение состояния движения механической системы может быть вызвано либо изменением действующих на нее внешних сил, либо изменением ее массы. Из этих же законов следует, что динамическими параметрами механической системы являются: инерциальные (массы m и моменты инерции I); силовые (силы Fij и моменты сил Mij); кинематические (линейные a и угловые e ускорения). Основные задачи динамики машин. 1. Прямая задача динамики – по заданному закону движения входного звена определяют силы, действующие на механизм, в том числе и усилия, возникающие в КП. Эта задача решается в вашем 2 ДЗ «Силовой расчет» с применением кинетостатики (составляют уравнения силового равновесия с учетом сил инерции по принципу Даламбээээра). 2. Обратная задача динамики - определение закона движения ведущего звена в зависимости от силового воздействия. Эта задача решается в самом объемном листе КП «Динамическое исследование основного механизма». 3. Балансировка и уравновешивание механизмов. 4. Виброзащита и виброизоляция. Классификация сил, действующих в механизмах. Силой называется мера механического воздействия одного материального тела на другое, характеризующая величину и направление этого воздействия. Т.е. сила - векторная величина, которая характеризуется величиной и направлением действия. Все силы, действующие в механизмах, условно подразделяются на:
|
|
|
| реальные | расчетные | ||
| На самом деле присутствуют в работе механизма | Силы, которые не существуют в реальности, а только используются в различных расчетах с целью их упрощения. Вводятся обычно равнодействующей. | ||
| Внешние – приложенные к механизму извне, т.е. действующие на исследуемую систему со стороны внешних систем и совершающие работу над системой. | Внутренние - действующие между звеньями механической системы Работа этих сил не изменяет энергии системы. | ||
| 1. Движущие силы и моменты, совершающие положительную работу. Эти силы и моменты прикладывают к звеньям механизма, которые называют ведущими. 2. Силы и моменты сопротивления, совершающие отрицательную работу - Силы полезного (технологического) сопротивления - возникающие при выполнении механической системой ее основных функций. Эти силы и моменты прикладывают к звеньям механизма, которые называют ведомыми. - Силы и моменты сопротивления среды (газа, жидкости) в которой движутся звенья механизма. Обычно малы по сравнению с другими, поэтому в дальнейшем их не учитываем. 3. Силы тяжести и упругости.. На отдельных участках движения механизма эти силы могут совершать как положительную, так и отрицательную работу, однако за полный кинематический цикл работа этих сил равна нулю, (за исключением тех случаев, когда сила тяжести является силой полезного сопротивления – механизмы подъемников, транспортеров эскалаторов и пр.) | Активные силы | 1. Силы реакций в КП. где - номер звена, на которое действует сила (рассматриваемое), - номер звена, со стороны которого рассматривается действие (отсоединенное). | 1. Силы инерции - предложены Д’Аламбером для силового расчета подвижных механических систем. При добавлении этих сил к внешним силам, действующим на систему, устанавливается квазистатическое равновесие системы и ее можно рассчитывать, используя уравнения статики (метод кинетостатики). 2. Приведенные (обобщенные) силы – силы, совершающие работу по обобщенной координате равную работе соответствующей реальной силы на эквивалентном перемещении точки ее приложения. |
| 4. Силы трения (диссипативные) - возникающие в месте связи в КП и определяемые условиями физико-механического взаимодействия между звеньями (работа всегда отрицательна, потери на силы трения уменьшают КПД механизма). Выводятся из класса внутренних сил. | |||
В зависимости от того какую работу совершают внешние силы за цикл движения машины различают три режима движения: разгон, торможение и установившееся движение. Циклом называют период времени или период изменения обобщенной координаты через который все параметры системы принимают первоначальные значения.
|
|
|
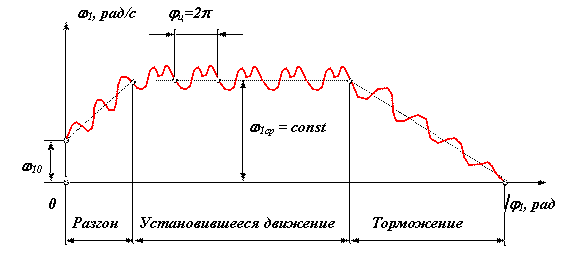
- Разгон => Адц Асц , А ц 0;
- Установившееся движение => Адц = Асц , А ц = 0;
- Торможение (выбег) => Адц Асц , А ц 0.
6.Динамическая модель. Приведение масс и моментов инерции при переходе к динамической модели.
В общей постановке динамика – изучение каких-либо процессов или явлений в функции времени. Динамическая модель – модель системы, предназначенная для исследования ее свойств в функции времени (или модель системы, предназначенная для исследования в ней динамических явлений). Механизм машинного агрегата обычно является многозвенной системой, нагруженной силами и моментами, приложенными к различным ее звеньям. Рассмотрим в качестве примера силовую установку, где ДВС через редуктор приводит в движение рабочую машину. Определение закона движения такой сложной многозвенной системы представляет собой сложную задачу, однако данный машинный агрегат имеет одну степень свободы. Это значит, что, прежде всего, необходимо определить закон движения всего лишь одного звена, которое будет являться начальным. Такая постановка задачи приводит к мысли, заменить весь сложный многозвенный механизм одним условным звеном. Если заданный механизм имеет звено, совершающее непрерывное вращательное движение, то именно его и целесообразно выбирать в качестве начального. При замене механизма динамической моделью необходимо выполнить следующие условия: 1. Закон движения входного звена механизма должен совпадать с законом движения модели его заменяющей. Т.е. кинематические характеристики модели и звена приведения механизма должны быть одинаковыми или положение модели в пространстве и положение звена приведения должны быть одинаковыми. 2. Модель должна быть нагружена условной силой или моментом, называемым приведенным моментом или силой и определяемым из условия равенства мгновенных мощностей модели и машинного агрегата. Т.е. или являются эквивалентом всей заданной нагрузки приложенной к машинному агрегату. 3. Модель должна обладать условной массой или моментом инерции, называемым приведенной массой или приведенным моментом инерции и определяемым из условия равенства кинетических энергий модели и машинного агрегата. Т.е. или являются эквивалентом все инерционности машинного агрегата. Т. о. замена механизма динамической моделью заключается в: 1. Замене всех реальных сил силовым фактором. 2. Замене масс всех звеньев приведенным инерциальным фактором. Замена сил и масс называется приведением, звено которое выбрано в качестве начального – звеном приведения. Если звено приведения совершает вращательное движение, то все силы приводятся к приведенному моменту, а массы – к приведенному моменту инерции, если звено приведения совершает поступательное движение или приведение осуществляется к точке, то все силы приводятся к приведенной силе, а массы – к приведенной массе. Приведение масс делают с той же целью, что и приведение сил: видоизменить и упростить динамическую схему механизма, т.е. прийти к соответствующей динамической модели, а, следовательно, и упростить решение уравнения движения. Если в качестве динамической модели принято начальное звено с обобщенной координатой  , то кинетическая энергия модели должна быть равна сумме кинетических энергий всех звеньев механизма, т.е. в основу приведения масс к начальному звену положено условие равенства кинетических энергий. Приведенным моментом инерции называется параметр динамической модели, кинетическая энергия которой равна сумме кинетических энергий реально движущихся звеньев.
, то кинетическая энергия модели должна быть равна сумме кинетических энергий всех звеньев механизма, т.е. в основу приведения масс к начальному звену положено условие равенства кинетических энергий. Приведенным моментом инерции называется параметр динамической модели, кинетическая энергия которой равна сумме кинетических энергий реально движущихся звеньев.
Запишем условие равенства кинетической энергии отдельного взятого звена, всего механизма и модели для отдельного звена: 
 (6.6)
(6.6) 
 где
где  для модели,
для модели,  для реальных звеньев механизма
для реальных звеньев механизма 
 (6.7) Передаточные функции в скобках не зависят от
(6.7) Передаточные функции в скобках не зависят от  , поэтому
, поэтому 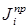 может быть определен далее в том случае, если закон движения модели (начального звена) неизвестен. При
может быть определен далее в том случае, если закон движения модели (начального звена) неизвестен. При  =
= 
 где
где  ,
,  Давайте определим приведенные моменты инерции
Давайте определим приведенные моменты инерции 
 Все эти моменты инерции не зависят от углового положения начального звена. Эта группа звеньев, связанных с динамической моделью линейными передаточными отношениями называется звеньями первой группы, а их моменты инерции – моментами инерции первой группы.
Все эти моменты инерции не зависят от углового положения начального звена. Эта группа звеньев, связанных с динамической моделью линейными передаточными отношениями называется звеньями первой группы, а их моменты инерции – моментами инерции первой группы.  Определим моменты инерции 2-го и 3-го звеньев
Определим моменты инерции 2-го и 3-го звеньев 

 Моменты инерции первой и второй группы звеньев и суммарный приведенный момент инерции рассматриваемой установки показан на рис. 6.7
Моменты инерции первой и второй группы звеньев и суммарный приведенный момент инерции рассматриваемой установки показан на рис. 6.7
|

7.Динамическая модель. Приведение сил и моментов при переходе к динамической модели. (см. рис. 6.7)
Положение механизма с W=1 вполне определяется одной координатой, которая называется обобщенной координатой. В качестве обобщенной координаты чаще всего принимают угловую координату звена, совершающего вращательное движение. В этом случае динамическая модель будет представлена в виде:  - обобщенная угловая координата модели
- обобщенная угловая координата модели  - угловая скорость модели
- угловая скорость модели  - суммарный приведенный момент (обобщенная сила - эквивалент всей заданной нагрузки, приложенной к механизму)
- суммарный приведенный момент (обобщенная сила - эквивалент всей заданной нагрузки, приложенной к механизму)  - суммарный приведенный момент инерции, являющийся эквивалентом инерционности механизма. В случае приведения, фактически действующие силы и моменты заменяем суммарным приведенным моментом, приложенным к динамической модели. Следует подчеркнуть, что сделанная замена не должна нарушить закона движения механизма, определяемого действием фактически приложенных сил и моментов. В основу приведения сил и моментов должно быть положено условие равенства элементарных работ, т.е. элементарная работа каждой силы на возможном перемещении точки ее приложения или момента на возможном угловом перемещении того звена, на котором он действует должна быть равна элементарной работе приведенного момента на возможном угловом перемещении динамической модели. Рассмотрим в качестве примера приведение сил и моментов, приложенных к звеньям машинного агрегата, назначив в качестве обобщенной координаты угловую координату
- суммарный приведенный момент инерции, являющийся эквивалентом инерционности механизма. В случае приведения, фактически действующие силы и моменты заменяем суммарным приведенным моментом, приложенным к динамической модели. Следует подчеркнуть, что сделанная замена не должна нарушить закона движения механизма, определяемого действием фактически приложенных сил и моментов. В основу приведения сил и моментов должно быть положено условие равенства элементарных работ, т.е. элементарная работа каждой силы на возможном перемещении точки ее приложения или момента на возможном угловом перемещении того звена, на котором он действует должна быть равна элементарной работе приведенного момента на возможном угловом перемещении динамической модели. Рассмотрим в качестве примера приведение сил и моментов, приложенных к звеньям машинного агрегата, назначив в качестве обобщенной координаты угловую координату  . Определим
. Определим  , заменяющий приложенную силу
, заменяющий приложенную силу  . По условию равенства элементарных работ
. По условию равенства элементарных работ  решив относительно искомой величины
решив относительно искомой величины  и разделив возможные перемещения на время, получим
и разделив возможные перемещения на время, получим  =
= 
 cos(
cos( ,
,  ), где cos(
), где cos(

 )=
)=  1
1  =
= 
 =
= 
 =
=  , где
, где 
 для решения на ЭВМ,
для решения на ЭВМ,  с использованием
с использованием  скоростей. Аналогично произведем приведение к динамической модели (звену 1) сил
скоростей. Аналогично произведем приведение к динамической модели (звену 1) сил  ,
,  , и
, и  .
.  =
=  cos(
cos( ,
,  ) = 0,0 т.к. cos(
) = 0,0 т.к. cos( ,
,  ) = 0.
) = 0.
 =
=  =
=  =
= 
 - проекция скорости центра масс
- проекция скорости центра масс  на ось у.
на ось у. 
 Подобным же образом найдем
Подобным же образом найдем  . Если алгебраически сложить все приведенные моменты, приложенные к начальному звену, то получим суммарный приведенный момент, который заменяет собой все силы и моменты, действующие на механизм.
. Если алгебраически сложить все приведенные моменты, приложенные к начальному звену, то получим суммарный приведенный момент, который заменяет собой все силы и моменты, действующие на механизм.  (6.5)
(6.5)
8.Уравнение движения машины. Угловая скорость звена приведения.
Рассмотрим случай, когда звено приведения совершает вращательное движение. Тогда вся система может быть представлена в виде звена, вращающегося с угловой скоростью wпр с ускорением eпр под действием момента Мпр и имеющее момент инерции Jпр (рисунок 2): 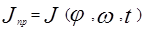

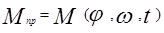 Запишем уравнение движения звена приведения
Запишем уравнение движения звена приведения  . Выполним преобразования, аналогичные тем, которые мы выполним при выводе уравнения |5|.
. Выполним преобразования, аналогичные тем, которые мы выполним при выводе уравнения |5|.  , где
, где  - угловое ускорение звена приведения.
- угловое ускорение звена приведения.  , где jпр – перемещение звена приведения;
, где jпр – перемещение звена приведения;  - угловая скорость звена приведения. Тогда
- угловая скорость звена приведения. Тогда  , откуда получаем
, откуда получаем  . |6| Уравнение |6| - дифференциальное уравнение движения машины в общем виде в случае вращательного движения звена приведения. Для случая Jпр=const,
. |6| Уравнение |6| - дифференциальное уравнение движения машины в общем виде в случае вращательного движения звена приведения. Для случая Jпр=const, 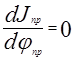 уравнение |6| принимает вид
уравнение |6| принимает вид  - уравнение движения звена приведения совершающего вращательное движение, если все звенья механизма вращающиеся и имеют постоянные массовые характеристики. Уравнение |5| более универсально. Уравнение |6| применяется только в случае, когда звено приведения совершает вращательное движение, а точка может принадлежать звену, совершающему любое движение. На практике чаще используют уравнение |6| в связи с тем, что силы и массы чаще приводят к валу двигателя – вращающемуся звену. Задача динамики машины чаще сводится к нахождению момента двигателя по заданному закону движения машины и некоторым силам, действующим на звенья машины.
- уравнение движения звена приведения совершающего вращательное движение, если все звенья механизма вращающиеся и имеют постоянные массовые характеристики. Уравнение |5| более универсально. Уравнение |6| применяется только в случае, когда звено приведения совершает вращательное движение, а точка может принадлежать звену, совершающему любое движение. На практике чаще используют уравнение |6| в связи с тем, что силы и массы чаще приводят к валу двигателя – вращающемуся звену. Задача динамики машины чаще сводится к нахождению момента двигателя по заданному закону движения машины и некоторым силам, действующим на звенья машины.
9.Установившееся движение. Коэффициент неравномерности хода. Назначение маховика.
О движении всех звеньев машины можно судить по движению одного звена, так как движение всех звеньев взаимосвязаны. Звено, по движению которого судят о характере работы машины, называется главным. За главное звено обычно принимают ведущее звено, так как оно непосредственно связано с двигателем. Чтобы иметь право судить по движению главного звена о движении остальных звеньев, необходимо учесть силы и моменты, действующие на все звенья механизма, а также массы и моменты инерции всех звеньев. Для этого все силы и массы приводят к главному звену. Приведенной силой (моментом) называется такая сила (момент) приложения к главному звену, которая развивает мощность равную сумме мощностей приводимых сил и моментов:  Если главное звено совершает поступательное движение, то удобно все силы и заменять эквивалентной по своему действию на механизм приведенной силой. Если главное звено вращается (что встречается гораздо чаще), то определяют приведенный момент. Приведенной массой (моментом инерции) называется такая условная масса (момент инерции), обладая которой главное звено имеет кинетическую энергию, равную сумме кинетических энергий приводимых масс и моментов инерции:
Если главное звено совершает поступательное движение, то удобно все силы и заменять эквивалентной по своему действию на механизм приведенной силой. Если главное звено вращается (что встречается гораздо чаще), то определяют приведенный момент. Приведенной массой (моментом инерции) называется такая условная масса (момент инерции), обладая которой главное звено имеет кинетическую энергию, равную сумме кинетических энергий приводимых масс и моментов инерции:  Здесь также удобно определять приведенную массу, если главное звено движется поступательно, и определять приведенный момент инерции, если главное звено совершает вращательное движение. После приведения сил и масс к главному звену определяется его истинный закон движения. Для установления истинного закона движения уравнение энергетического баланса записывается в дифференциальной форме, которое в данном случае носит название уравнения движения машины.
Здесь также удобно определять приведенную массу, если главное звено движется поступательно, и определять приведенный момент инерции, если главное звено совершает вращательное движение. После приведения сил и масс к главному звену определяется его истинный закон движения. Для установления истинного закона движения уравнение энергетического баланса записывается в дифференциальной форме, которое в данном случае носит название уравнения движения машины.  Дальнейшее решение задачи осуществляется интегрированием уравнения движения машины:
Дальнейшее решение задачи осуществляется интегрированием уравнения движения машины:  Из-за несоответствия характеристики двигателя и приведенного момента происходит отклонение истинного закона движения главного звена от первоначально заданного, происходят колебания угловой скорости.
Из-за несоответствия характеристики двигателя и приведенного момента происходит отклонение истинного закона движения главного звена от первоначально заданного, происходят колебания угловой скорости.  Рисунок 32. Эти колебания оцениваются коэффициентом неравномерности хода. Коэффициент неравномерности хода определяется для цикла установившегося движения, обычно обозначается δ и определяется следующей формулой:
Рисунок 32. Эти колебания оцениваются коэффициентом неравномерности хода. Коэффициент неравномерности хода определяется для цикла установившегося движения, обычно обозначается δ и определяется следующей формулой:  Опыт эксплуатации машин показывает, что на качество работы машины в большей степени влияет величина колебаний скорости главного звена, а не закон, по которому эти колебания происходят. Поэтому решение задачи обычно сводится к определению коэффициента неравномерности хода δ, после чего он сравнивается с допустимой величиной [δ] для данного типа машин. Решение уравнения движения машины (интегрирование) и определение коэффициента неравномерности хода обычно производят графическими методами. Если коэффициент неравномерности хода окажется больше допустимого для данного типа машин, то необходимо отрегулировать ход машины, т.к. колебания скорости вызывают дополнительные динамические нагрузки на детали машин, а также ухудшают рабочий процесс машины. Простейшим способом регулирования хода машины является постановка маховика. Маховик – это обычно колесо, имеющее массивный обод. Обладая значительной массой, маховик играет роль аккумулятора кинетической энергии. При избытке энергии у двигателя (когда момент двигателя больше приведенного момента) маховик накапливает эту энергию, при недостатке – отдает ранее накопленную энергию механизму. За счет этого происходит уменьшение колебаний скорости главного звена. Чем больше масса и скорость маховика, тем меньше коэффициент неравномерности хода. С целью уменьшения массы маховика целесообразно ставить его на наиболее быстро вращающееся звено.
Опыт эксплуатации машин показывает, что на качество работы машины в большей степени влияет величина колебаний скорости главного звена, а не закон, по которому эти колебания происходят. Поэтому решение задачи обычно сводится к определению коэффициента неравномерности хода δ, после чего он сравнивается с допустимой величиной [δ] для данного типа машин. Решение уравнения движения машины (интегрирование) и определение коэффициента неравномерности хода обычно производят графическими методами. Если коэффициент неравномерности хода окажется больше допустимого для данного типа машин, то необходимо отрегулировать ход машины, т.к. колебания скорости вызывают дополнительные динамические нагрузки на детали машин, а также ухудшают рабочий процесс машины. Простейшим способом регулирования хода машины является постановка маховика. Маховик – это обычно колесо, имеющее массивный обод. Обладая значительной массой, маховик играет роль аккумулятора кинетической энергии. При избытке энергии у двигателя (когда момент двигателя больше приведенного момента) маховик накапливает эту энергию, при недостатке – отдает ранее накопленную энергию механизму. За счет этого происходит уменьшение колебаний скорости главного звена. Чем больше масса и скорость маховика, тем меньше коэффициент неравномерности хода. С целью уменьшения массы маховика целесообразно ставить его на наиболее быстро вращающееся звено.
10.Задача динамического анализа. Определение средней угловой скорости ведущего звена и коэффициента неравномерности хода по диаграмме Виттенбауэра.
Т=Ιω²/2 Т=Т(φ) Ι=I(φ)
ω=√2Т/I=√2yµT/xµy=√2µT/µy·√tgψ
ω²=2tgψµT/µy tgψ= ω²µy/2µT
11.Определение максимальной и минимальной угловой скорости по диаграмме Виттенбауэра в общем виде.
ω¡²=2tgψ¡µT/µy
ωmax=ωcp(1+δ/2) ωmin=ωcp(1-δ/2) tgψmax= ωcp²(1+δ)µy/2µT
ω²max=ω²cp(1+δ) ω²min=ω²cp(1-δ) tgψmin= ωcp²(1-δ)µy/2µT При проведении касательной не обязательно знать нач.коорд.-она уходит далеко за пределы чертежа на пересечении касательных.
12.Задача динамического синтеза. Графический метод расчета маховика по диаграмме Виттенбауэра.
Метод Виттенбауэра основан на построении диаграммы изменения кинетической энергии механизма от приведенного момента инерции его звеньев Т = f (I), т. е. диаграммы энергомасс. Построение диаграммы энергомасс выполняют в такой последовательности. 1. Рассчитываются и строятся графики DА = Адс –Апс в той же последовательности (метод Мерцалова). 2. Определяется приведенный момент инерции механизма по зависимости  (5.36) где mi – масса i-го звена, кг; Vsij – скорость центра масс i-го звена в j-м положении, м; Isi – момент инерции i-го звена относительно центра масс, кг×м2; wiJ – угловая скорость i-го звена в j-м положении, с–1; wп – угловая скорость вала установки маховика, с–1. По зависимостям (5.11), (5.12) и (5.13) подсчитывается момент инерции всех звеньев для 12 положений механизма и результаты заносятся в таблицу, аналогичную табл.5.5. Полученные данные суммируются в каждом положении механизма и определяется величина приведенного момента инерции звеньев механизма в соответствии с формулой (5.36). 3. Выбирается масштаб mI и по данным табл.5.5 строится график Iп=f(j) изменения приведенного момента инерции за один цикл работы механизма, как показано на рис. 5.6, а. 4. Строится диаграмма энергомасс. Для этого исключается графически параметр j из диаграмм DA = f (j) и Iп = f (j). Описывается последовательность построения диаграммы энергомасс. Последовательность исключения параметра j из графиков DA = =f(j) и Iп = f(j), построенных для кривошипно-шатунного механизма, показана на рис.5.6 а,б. 5. Определяются углы ymax и ymin наклона касательных к диаграмме энергомасс:
(5.36) где mi – масса i-го звена, кг; Vsij – скорость центра масс i-го звена в j-м положении, м; Isi – момент инерции i-го звена относительно центра масс, кг×м2; wiJ – угловая скорость i-го звена в j-м положении, с–1; wп – угловая скорость вала установки маховика, с–1. По зависимостям (5.11), (5.12) и (5.13) подсчитывается момент инерции всех звеньев для 12 положений механизма и результаты заносятся в таблицу, аналогичную табл.5.5. Полученные данные суммируются в каждом положении механизма и определяется величина приведенного момента инерции звеньев механизма в соответствии с формулой (5.36). 3. Выбирается масштаб mI и по данным табл.5.5 строится график Iп=f(j) изменения приведенного момента инерции за один цикл работы механизма, как показано на рис. 5.6, а. 4. Строится диаграмма энергомасс. Для этого исключается графически параметр j из диаграмм DA = f (j) и Iп = f (j). Описывается последовательность построения диаграммы энергомасс. Последовательность исключения параметра j из графиков DA = =f(j) и Iп = f(j), построенных для кривошипно-шатунного механизма, показана на рис.5.6 а,б. 5. Определяются углы ymax и ymin наклона касательных к диаграмме энергомасс:  Рис.5.6. Диаграммы изменения: а – приведенного момента инерции; б – избыточной работы; в – энергомасс за цикл работы.
Рис.5.6. Диаграммы изменения: а – приведенного момента инерции; б – избыточной работы; в – энергомасс за цикл работы.  ; (5.37)
; (5.37)  . (5.38) 6. Проводятся под этими углами касательные в высшей и низшей точках кривой Виттенбауэра и находится длина отрезка kl, отсекаемого на оси ординат. Искомый момент инерции маховых масс определяется по формуле
. (5.38) 6. Проводятся под этими углами касательные в высшей и низшей точках кривой Виттенбауэра и находится длина отрезка kl, отсекаемого на оси ординат. Искомый момент инерции маховых масс определяется по формуле  . (5.39) 7. Производится расчет размеров и массы маховика так же, как и по методу Н.И. Мерцалова
. (5.39) 7. Производится расчет размеров и массы маховика так же, как и по методу Н.И. Мерцалова
13.Построение закона движения ведущего звена механизьма по диаграмме Виттенбауэра и определение ускорений для различных положений ведущего звена.
µ(dω/dφ)= µω/Hµφ
ω=(ωcp-y·µω)
ε=ω(dω/dφ)· µ(dω/dφ)
14.Синтез кулачковых механизьмов. Условия проектирования. Динамические условия работоспособности кулачковых механизьмов.
Метод обращения движения. Кулачок и толкатель мысленно вращают со скоростью w(кулачка) на встечу направления этой скорости Результат: кулачок неподвижен,толкатель обегает кулачок со скоростью –w(кулачка) Условия: Существует множество кулачковых механизмов,удовлетворяющих заданным законам движения толкателя.Лучшее решение то,при котором: 1)механизм имеет наименьшие размеры 2)удовлетворяет конструктивным и прочностным требованиям При динамическом синтезе по заданным минимальным углам передачи движения определяют радиус минимальной шайбе r(o) Основные размеры кулачковых механизмов определяются из кинематических,динамических условий: Механизм должен воспроизводить закон заданного движения. Динамические условия:высокий КПД и не должно быть заклинивания. Конструктивные условия:достаточная прочно
|
|
|


