 |
Модуляция потоков энергичных частиц гидромагнитными волнами.
|
|
|
|
Предположим, что существует фоновое высыпание частиц, обусловленное, например, диффузией в конус потерь. Найдем глубину модуляции высыпающегося потока в зависимости от амплитуды геомагнитных пульсаций, которые можно связывать со стоячей альвеновской волной, захваченной между магнитосопряженными участками ионосфер различных полушарий. Известно, что направляемые альвеновские волны не сопровождаются сжатием магнитного поля. Однако, в неоднородном магнитном поле каждая колеблющаяся магнитная силовая линия будет испытывать субстанциональные сжатия и разрежения. Магнитное поле в такой колеблющейся трубке меняется по закону:
, (4)
где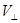 
- колебательная скорость трубки. Плазма, вмороженная в трубку, колеблющуюся в меридиальной плоскости, испытывает периодическое нагревание и охлаждение, что приводит к вариациям частиц в трубке с периодом ее поперечных колебаний. Вариации потока частиц на уровне ионосферы существенно зависят от характера изменений питч-углового распределения частиц. Рассмотрим четыре случая, отличающихся характером изменения функции распределения, а также энергией частиц. Вначале найдем связь глубины модуляции с амплитудой колебаний в экваториальной плоскости 
, а затем с амплитудой пульсаций на поверхности Земли.
3.1.1. Случай быстрой изотропизации. Относительное изменение потока может быть найдено из теоремы Лиувилля и определяется выражением:
. (5)
где 
- поток частиц в единице телесного угла и в единичном интервале энергий 
, 
- возмущенные величины.
|
|
|
Поперечные радиальные колебания трубки сопровождаются изменением ее объема. Предполагая процесс адиабатическим, из уравнения адиабаты 
находим связь между изменением энергии частиц и изменениями объема:
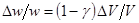. (6)
Рассмотрим первую гармонику колебаний. Считаем для простоты, что объем трубки пропорционален 
(
- геоцентрическое рассеяние до трубы в экваториальной плоскости в радиусах Земли). Имеем:
. (7)
Подставляя (7.3) и (7.4) в (7.2), получаем для зависимости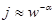 
. (8)
Последнее равенство написано для 
, 
.
3.1.2. Случай сохранения адиабатических инвариантов. Этот случай, вероятно, реализуется в спокойное время вдали от ярких форм сияний. Высыпание частиц в ионосферу связано при этом с сокращением магнитных силовых линий в процессе стационарной конвекции магнитосферной плазмы. Хотя с приближением магнитной силовой линии к Земле питч-углы заряженных частиц увеличиваются, конус потерь увеличивается еще быстрее. Высыпающийся поток примерно равен 
, где 
и 
- концентрация частиц и скорость их радиального дрейфа в экваториальной плоскости. Модуляция потока имеет вид:
. (9)
Где 
- возмущение скорости, связанное с гидромагнитной волной;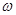 
- частота волны; 
- радиус Земли. Полагая частоту равной частоте резонансных колебаний магнитной трубки (
), получаем:
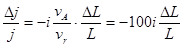. (10)
Последнее равенство выполняется при характерных значениях 
км/с и 
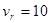км/с.
3.1.3. Модуляция инкремента нарастания свистовой моды. Предполагается, что фоновое высыпание вызвано диффузией частиц в конус потерь из-за резонансного взаимодействия со свистовой модой. Эта мода непрерывно генерируется благодаря анизотропии распределения электронов по питч-углам. Инкремент нарастания свистовой моды зависит от внешнего магнитного поля. Гидромагнитная волна, возмущая магнитное поле, изменяет инкремент свистовой моды, что приводит к модуляции коэффициента диффузии и, следовательно, к модуляции высыпающегося потока. В качестве гидромагнитной волны мы принимали магнитозвуковую. Однако, как видно из формулы (4), направляемая альвеновская волна в неоднородном поле также сопровождается субстанциональными изменениями магнитного поля.
|
|
|
Если диффузия в конус потерь не слишком велика, высыпающийся поток равен:
, (11)
где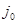 
- фоновый поток; 
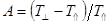- коэффициент анизотропии электронов по питч-углам; 
и 
-температуры электронов поперек и вдоль внешнего магнитного поля; 
-амплитуда малых вариаций. Принимая для экваториальной плоскости 
, 
и считая колебания малыми, получаем из (11) глубину модуляции
. (12)
Сравнение (12) с (8) показывает, что коэффициент анизотропии 
обеспечивает диффузию, промежуточную между сильной и слабой. Уменьшение приводит к уменьшению диффузии и к увеличению глубины модуляции. В данном случае глубина увеличивается за счет уменьшения фононовоо потока.
3.1.4. Модуляция потоков высокоэнергичных частиц. При рассмотрении трех предыдущих случаев предполагалось, что частицы колеблются вместе с магнитной трубкой. При характерном диаметре трубки в экваториальной плоскости 
и периоде колебаний 
условие сохранения частиц в трубке выполняется для энергий 
. Частицы больших энергий будут протекать через трубку (вследствие градиентного дрейфа), почти не реагируя на ее колебания. Можно считать, что магнитная силовая трубка колеблется на неподвижном фоне энергичных частиц. Колеблющаяся трубка, подобно зонду, будет проектировать в свое основание частицы из разных областей ионосферы. Магнитосфера заселена энергичными частицами неоднородно. Поэтому поток частиц, высыпающихся из трубки, будет флуктуировать. Полагая, что фоновый поток энергичных частиц меняется по закону:
|
|
|
, (13)
получаем глубину модуляции:
. (14)
Последнее равенство выполняется при характерных значениях 
, 
, 
. Изменение потока происходит в фазе или противофазе с может быть выражено через магнитное поле стоячей альвеновской волны:
, (15)
где 
-северная компонента поля над ионосферой; 
и 
внешнее магнитное поле в экваториальной плоскости и на уровне ионосферы соответственно. При выводе (15) предполагалось, что альвеновская скорость постоянна вдоль силовой трубки, трубка совершает колебания на основной гармонике, концы трубки закреплены на ионосфере.
Поле не проникает ниже ионосферы, так как полностью экранируется педерсеновскими токами. Под ионосферой чувствуется магнитное возмущение 
, связанное с холловскими токами:
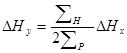, (16)
где 
и 
- проинтегрированные по высоте холловская и педерсеновская проводимости; поле 
считается положительным, если оно направлено на восток. Подставляя (16) в (15) и полагая 
, 
и 
, получаем:
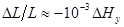, (17)
где выражено в нТл.
Возвращаясь к выражениям (8), (10), (12) и (14), запишем с учетом (17) относительную вариацию потока:
, (18)
где величина коэффициента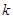 
для четырех рассмотренных случаев принимает соответственно решения 
; 
и 
. Наиболее благоприятен для модуляции случай 2 (сохранение инвариантов); при амплитуде колебаний 
получаем в этом случае 
. Случаи 1,3 и 4 способны вызвать только 10 –20 %-ную модуляцию потоков частиц. Напомним, что случай 1 (быстрая изотропизация) дает нижний предел для глубины модуляции низкоэнергичных (<30 кэВ) частиц; уменьшение питч-угловой диффузии приведет к увеличению глубины модуляции.
|
|
|
Следует отметить своеобразие случая 4. Несмотря на почти полное отсутствие взаимодействия колеблющейся трубки с высокоэнергичными частицами, высыпающийся поток испытывает довольно сильную модуляцию.
|
|
|
